Ответ оценивается отметкой «4»,

- если удовлетворяет в основном требованиям на оценку «5»,

- но при этом имеет один из недостатков:

- в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

- допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя;

- не решена задача в вопросе №4 (но при этом первые три вопроса изложены в полном объёме) или во втором вопросе не произведено доказательство (но три вопроса - 1, 3, 4 изложены в полном объёме).

Отметка «3» ставится в следующих случаях:

- неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;

- имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, решении задач, исправленные после нескольких наводящих вопросов учителя;

- ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме (вопросы 1 и 3 экзаменационного билета);

- при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

- не раскрыто основное содержание учебного материала;

- обнаружено незнание обучающимся большей или наиболее важной части учебного материала;

- допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

БИЛЕТ №1

1. Параллелограмм (определение). Формула для нахождения площади параллелограмма. 2. Свойства углов четырехугольника, вписанного в окружность (доказательство). 3. Задача 1. В трапеции известно, что , и . Найдите угол Ответ дайте в градусах. 4. Задача 2. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Докажите, что площади треугольников АОВ и COD равны.

БИЛЕТ №2.

1. Трапеция (определение). Площадь трапеции (формула). 2. Свойство сторон описанного четырехугольника (доказательство). 3. Задача 1. Периметр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба. 4. Задача 2. Катет и гипотенуза прямоугольного треугольника соответственно равны 20 и 52. Найдите высоту, проведённую к гипотенузе.

БИЛЕТ №3

1. Прямоугольник (определение). Площадь прямоугольника (формула). 2. Теорема об окружности, вписанной в треугольник (доказательство). 3. Задача 1. Сторона треугольника проходит через центр описанной около него окружности. Найдите , если . Ответ дайте в градусах. 4. Задача 2. Высота АН ромба ABCD делит сторону CD на отрезки DH = 20 и СН = 5. Найдите высоту ромба.

БИЛЕТ № 4 1. Ромб, квадрат (определения). Площадь ромба (формула). 2. Теорема об окружности, описанной около треугольника (доказательство) 3. Задача 1. Синус острого угла А прямоугольного треугольника равен 0,6. Найдите косинус и тангенс угла А. 4. Задача 2. Прямая, параллельная стороне АС треугольника ABC, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 13, АС = 65, NC = 28. БИЛЕТ № 5 1. Подобные треугольники. Коэффициент подобия. 2. Свойство противоположных сторон и углов параллелограмма (доказательство). 3. Задача 1. 4. Задача 2. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке K. Найдите периметр параллелограмма, если ВК = 3, CK = 19. БИЛЕТ № 6 Средняя линия треугольника (определение и свойства). Основное тригонометрическое тождество (доказательство). Задача 1. Используя данные рисунка, найдите угол АВС. Задача 2. Биссектрисы углов В и С параллелограмма ABCD пересекаются в точке М стороны AD. Докажите, что М — середина AD.

БИЛЕТ № 7

1. Синус, косинус и тангенс острого угла прямоугольного треугольника (определения, рисунок). 2. Свойство диагоналей параллелограмма (доказательство). 3. Задача 1. 4. Задача 2. Основания ВС и AD трапеции ABCD равны соответственно 3 и 12, BD=6. Докажите, что треугольники CBD и BDA подобны.

БИЛЕТ № 8

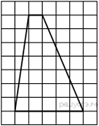
1. Свойство высоты треугольника, проведенной из вершины прямого угла. 2. Площадь треугольника (доказательство) 3. Задача 1. На клетчатой бумаге с размером клетки 1х1 изображён треугольник . Найдите длину его средней линии, параллельной стороне . 4. Задача 2. Точка Н является основанием высоты, проведённой из вершины прямого угла В треугольника ABC к гипотенузе АС. Найдите АВ, если АН = 10, АС = 40.

БИЛЕТ № 9

1. Центральный и вписанный углы (определения, свойства). 2. Теорема Пифагора (доказательство). 3. Задача 1. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.   4. Задача 2. Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны АВ и CD в точках Р и Т соответственно. Докажите, что BP = DT.

БИЛЕТ № 10

1. Теорема Фалеса (формулировка, рисунок). 2. Теорема о средней линии треугольника (доказательство) 3. Задача 1. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите ее площадь. 4. Задача 2. Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 12, DC = 48, АС = 35.

БИЛЕТ № 11

1. Признаки параллелограмма (формулировки, рисунки). 2. Свойства отрезков касательных к окружности, проходящих через одну точку (доказательство) 3. Задача 1. На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь. 4. Задача 2. Сторона ВС параллелограмма ABCD вдвое больше стороны АВ. Точка Е — середина стороны ВС. Докажите, что АЕ — биссектриса угла BAD.

БИЛЕТ № 12

1. Вписанная окружность 2. Теорема об отношении площадей двух подобных треугольников (доказательство) 3. Задача 1. Косинус острого угла В прямоугольного треугольника равен 0,8. Найдите синус и тангенс угла В. 4. Задача 2. Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 8, BF = 15.

БИЛЕТ № 13

1. Описанная окружность 2. Свойства биссектрисы угла (доказательство) 3. Задача 1. 4. Задача 2. Биссектрисы углов B и C трапеции ABCD пересекаются в точке О, лежащей на стороне AD. Докажите, что точка О равноудалена от прямых АВ, ВС и CD.

БИЛЕТ № 14

1. Медианы в треугольнике (перечислить свойства: 1) в каком отношении делится каждая медиана точкой их пересечения; 2) свойство медианы треугольника, выходящей из прямого угла; 3) на какие части медиана делит произвольный треугольник). 2. Свойство касательной к окружности (доказательство). 3. Задача 1. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь. 4. Задача 2. Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны ВС и AD в точках К и М соответственно. Докажите, что BK = DM.

БИЛЕТ № 15 1. Определение трапеции. Равнобедренная и прямоугольная трапеции. 2. Первый признак подобия треугольников (доказательство) 3. Задача 1. В па­рал­ле­ло­грам­ме ABCD про­ве­де­на диа­го­наль AC. Угол DAC равен 47°, а угол CAB равен 11°. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма ABCD. Ответ дайте в градусах. 4. Задача 2. Прямая, параллельная стороне АС треугольника ABC, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 15, АС = 25, NC = 22. БИЛЕТ № 16 1. Значение синуса, косинуса и тангенса для углов 30, 45, 60 градусов. 2. Теорема-задача о свойстве биссектрисы треугольника. 3. Задача 1. В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.   4. Задача 2. Радиус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду AC в точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ра­ди­ус окружности равен 5 см.

БИЛЕТ № 17

1. Утверждения о пропорциональных отрезках в прямоугольном треугольнике 2. Теорема об отрезках пересекающихся хорд окружности (доказательство) (доказательство) 3. Задача 1. Сторона равностороннего треугольника равна . Найдите медиану этого треугольника. 4. Задача 2. Основания ВС и AD трапеции ABCD равны соответственно 3 и 12, BD=6. Докажите, что треугольники CBD и BDA подобны.

БИЛЕТ № 18

1. Формула Герона. 2. Теорема о площади параллелограмма 3. Задача 1. Точка O — центр окружности, на которой лежат точки A, B и C таким образом, что OABC — ромб. Найдите угол OAB. Ответ дайте в градусах.   4. Задача 2. Высота АН ромба ABCD делит сторону CD на отрезки DH = 20 и СН = 5. Найдите высоту ромба.

БИЛЕТ № 19

1. Отношение площадей треугольников, имеющих по одному равному углу (формулировка, рисунок). 2. Площадь трапеции (доказательство). 3. Задача 1. В окруж­но­сти с цен­тром O AC и BD — диаметры. Цен­траль­ный угол AOD равен 128°. Най­ди­те вписанный угол ACB. Ответ дайте в градусах. 4. Задача 2. Катеты прямоугольного треугольника равны 21 и 28. Найдите высоту, проведённую к гипотенузе.

БИЛЕТ № 20

1. Отношение площадей треугольников, имеющих равные высоты. 2. Свойство перпендикулярности диагоналей ромба. 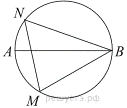3. Задача 1. На окруж­но­сти по раз­ные стороны от диа­мет­ра AB взяты точки M и N. Известно, что ∠ NBA = 41°. Най­ди­те угол NMB. Ответ дайте в градусах. 4. Задача 2. Прямая, параллельная стороне АС треугольника ABC, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 13, АС = 65, NC = 28.

БИЛЕТ № 21

1. Прямоугольник. Квадрат (определения, свойства). 2. Свойства углов четырехугольника, вписанного в окружность (доказательство). 3. Задача 1. Найдите пло­щадь трапеции, изображённой на рисунке.   4. Задача 2. Биссектрисы углов В и С параллелограмма ABCD пересекаются в точке М стороны AD. Докажите, что М — середина AD.

БИЛЕТ № 22

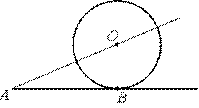
1. Свойства серединного перпендикуляра к отрезку. 2. Теорема Пифагора. 3. Задача 1. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 24, AO = 26. 4. Задача 2. Точка Н является основанием высоты, проведённой из вершины прямого угла В треугольника ABC к гипотенузе АС. Найдите АВ, если АН = 10, АС = 40.