Сущность теоремы Чебышева

Неравенство и теорема Чебышева. Сущность и значение теоремы Чебышева. Теорема Бернулли.

 

Неравенство Чебышева, используемое справедливо как для непрерывных, так и для дискретных случайных величин. Докажем его для дискретных случайных величин.

Неравенство Чебышева. Р( | X – M (X)| < ε) ≥ D (X) /ε2.

Доказательство. Пусть Х задается рядом распределения

Х х 1 х 2 … хп

р р 1 р 2 … рп

Так как события | X – M (X)| < ε и | X – M (X)| ≥ ε противоположны, то р (| X – M (X)| < ε) +

+ р (| X – M (X)| ≥ ε) = 1, следовательно, р (| X – M (X)| < ε) = 1 - р (| X – M (X)| ≥ ε). Найдем

р (| X – M (X)| ≥ ε).

D (X) = (x 1 – M (X))2 p 1 + (x 2 – M (X))2 p 2 + … + (xn – M (X))2 pn. Исключим из этой суммы те

слагаемые, для которых | X – M (X)| < ε. При этом сумма может только уменьшиться, так

как все входящие в нее слагаемые неотрицательны. Для определенности будем считать,

что отброшены первые k слагаемых. Тогда

D (X) ≥ (xk+ 1 – M (X))2 pk+ 1 + (xk+ 2 – M (X))2 pk +2 + … + (xn – M (X))2 pn ≥ ε2 (pk+ 1 + pk+ 2 + … + pn).

Отметим, что pk+ 1 + pk+ 2 + … + pn есть вероятность того, что | X – M (X)| ≥ ε, так как это

сумма вероятностей всех возможных значений Х, для которых это неравенство

справедливо. Следовательно, D (X) ≥ ε2 р (| X – M (X)| ≥ ε), или р (| X – M (X)| ≥ ε) ≤ D (X) / ε2.

Тогда вероятность противоположного события p( | X – M (X)| < ε) ≥ D (X) / ε2, что и требо-

валось доказать.

Теорема Чебышева

Если Х₁, Х₂, …,Х_n..- попарно независимые случайные величины, причем диспер­сии их равномерно ограничены (не превышают постоян­ного числа С), то, как бы мало ни было положительное число ε, вероятность неравенства

P (÷ (Х₁+Х₂ + …+Х_n) / n - (M(Х₁)+M(Х₂)+ …+M(Х_n))/n | < ε

будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, в условиях теоремы

P (÷ (Х₁+Х₂ + …+Х_n) / n - (M(Х₁)+M(Х₂)+ …+M(Х_n))/n | < ε)=1.

Теорема Чебышева утверждает:

1. Рассматривается достаточно большое число незави­симых случайных величин, имеющих ограниченные ди­сперсии,

2. Почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их ма­тематических ожиданий будет по абсолютной величине сколь угодно малым.

Можно сформулировать тео­рему Чебышева для рассматриваемого частного случая.

“Если Х₁, Х₂, …,Х_n..- попарно независимые случай­ные величины, имеющие одно и то же математическое ожидание а, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было число ε > О, ве­роятность неравенства

P (÷ (Х₁+Х₂ + …+Х_n) / n – a | < ε будет как угодно близка к единице, если число случай­ных величин достаточно велико”.

Другими словами, в условиях теоремы

P (÷ (Х₁+Х₂ + …+Х_n) / n – a | < ε) = 1.

Сущность теоремы Чебышева

Хотя от­дельные независимые случайные величины могут прини­мать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случай­ных величин с большой вероятностью принимает значе­ния, близкие к определенному постоянному числу, а именно к числу

(М (Xj) + М (Х₂) +… + М (Х„))/п или к числу а в частном случае.

Иными словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.

Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных вели­чин, но можно предвидеть, какое значение примет их среднее арифметическое.

Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной, величины.

Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.

Теорема Чебышева справедлива не только для дискрет­ных, но и для непрерывных случайных величин; она является примером, подтверждающим справедли­вость учения о связи между случайностью и необходимостью.

Значение теоремы Чебышева для практики Приведем примеры применения теоремы Чебышева к решению практических задач.

Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифме­тическое принимают в качестве искомого размера. Рассмотрим результаты каждого из­мерения как случайные величины Х₁, Х₂, …,Х_n К этим величинам можно применить теорему Чебышева, если:

1) Они попарно независимы.

2) имеют одно и то же ма­тематическое ожидание,

3) дисперсии их равномерно огра­ничены.

Первое требование выполняется, если результат каж­дого измерения не зависит от результатов остальных.

Второе требование выполняется, если измерения произ­ведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы и равны истинному размеру а.

Третье требо­вание выполняется, если прибор обеспечивает определен­ную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их огра­ничено.

Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева: при достаточно большом п вероятность неравенства

| (Х₁ + Х_я+…+Х„)/п - а |< ε как угодно близка к единице.

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов.Уже из приведенных примеров можно заключить, что для практики теорема Чебышева имеет неоценимое значение.

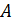Теорема Бернулли. Если в каждом из независимых испытаний вероятность появления события постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Другими словами, если — сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство

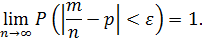
Доказательство. Обозначим через дискретную случайную величину — число появлений события в первом испытании, через — во втором,..., — в -м испытании. Ясно, что каждая из величин может принять лишь два значения: 1 (событие 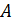наступило) с вероятностью и 0 (событие не появилось) с вероятностью .

Можно ли применить к рассматриваемым величинам теорему Чебышева? Можно, если случайные величины попарно независимы и дисперсии их ограничены. Оба условия выполняются Действительно, попарная независимость величин следует из того, что испытания независимы. Дисперсия любой величины равна произведению ; так как , то произведение не превышает 1/4[1] и, следовательно, дисперсии всех величин ограничены, например, числом .

Применяя теорему Чебышева (частный случай) к рассматриваемым величинам, имеем

Приняв во внимание, что математическое ожидание 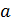каждой из величин (т.е. математическое ожидание числа появлений события в одном испытании) равно вероятности наступления события, получим

Остается показать, что дробь

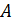равна относительной частоте появлений события в испытаниях. Действительно, каждая из величин при появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма 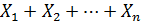равна числу появлений события в испытаниях, а значит,

Учитывая это равенство, окончательно получим

 

Среднее квадратическое отклонение. Среднее квадратическое отклонение суммы взаимно независимых случайных величин. Одинаково распределенные взаимно независимые случайные величины. Начальные и центральные теоретические моменты

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение. Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:

Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность 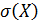совпадает с размерностью . Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если выражается в линейных метрах, то 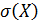будет выражаться также в линейных метрах, a — в квадратных метрах.