Цель работы: проанализировать воздействие двух точечных источников 1 и 2 тепла на пластину, приведенную на рисунке 33.
 Тип анализа
| Нестационарный тепловой анализ конструкции |
| Тип используемого конечного элемента | Двумерный твердотельный (Solid) |
| Тип граничных условий | Конвекция, точечные нелинейные источники тепла |
| Возможности | Нелинейная конвекция и тепловой источник |
Рис. 33
Порядок выполнения работы:
1. Определяем тип анализа:
MAIN MENU => PREFERENCES… => THERMAL => ОК.
2. Выбираем тип используемого элемента, задаём его толщину и определяемся со свойствами материала:
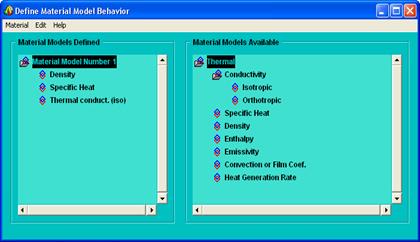Тип элементов: M.M. => PREPROCESSOR => ELEMENT TYPE => ADD/EDIT/DELETE => ADD… => THERMAL SOLID QUAD 4 NODE 55 => OK => CLOSE. Задаем материал: M.M. => PREPROCESSOR => MATERIAL PROPS => MATERIAL MODELS. Затем, следуя цифрам на рисунке 33, выполняем действия:
1. Двойным нажатием мыши на указанные папки выполняем:
THERMAL => CONDUCTIVITY => ISOTROPIC. В окне CONDUCTIVITY FOR MATERIAL NUMBER 1 в поле KXX задаем 50.
2. Двойным нажатиемраскрываем SPECIFIC HEAT и присваиваем C значение 30.
3. Аналогично раскрываем DENSITY и в поле DENS задаем 2788.
3. Строим деталь, которая будем представлять собой пластину размером 0,3´0,15 метра:
M.M. => PREPROCESSOR => -MODELING– CREATE=> –AREAS– RECTANGLE => BY DIMENSIONS… и задаем координаты X1, X2 и Y1, Y2 равные 0, 0.3 и 0, 0.15 соответственно. Нажимаем ОК.
4. Определяем точки на поверхности пластины, на которых будут находиться источники тепла: M.M. => PREPROCESSOR => –MODELING– CREATE => KEYPOINTS => HARD PT ON AREA => HARD PT BY COORD => выделяем поверхность на которой будет находится точка => OK=> указываем координаты 0.075, 0.5, 0 => HARD PT BY COORD => выделяем поверхность на которой будет находится точка => OK => указываем координаты 0.225, 0.1, 0.
|
|
5. Разбиваем конструкцию на конечные элементы:
А. Сначала задаем размер конечных элементов:
M.M. => PREPROCESSSOR => –MESHING– SIZE CNTRLS => –MANUAL SIZE– –GLOBAL– SIZE и переменной SIZE присваиваем значение 0.025, нажимаем ОК.
Б. Производим разбиение:
M.M. => PREPROCESSOR => –MESHING– MESH => –AREAS– FREE => PICK ALL.
6. Выбираем тип анализа:
SOLUTION => –ANALYSIS TYPE– NEW ANALYSIS… => TRANSIENT => OK => OK.
7. Задаем температуру окружающей среды и коэффициент теплопроводности:
M.M. => SOLUTION => –LOADS– APPLY => CONVECTION => ON AREAS=> присвоим: [SFA] APPLY FILM COEF ON AREAS=NEW TABLE и VAL2I BULK TEMPERATURE = 20 => OK=> NAME OF NEW TABLE = TEM => OK => I, J, K = 3, 1, 1 соответственно => OK. В соответствии с рисунком 34 заполняем поля таблицы 1 и потом: FILE => APPLY/QUIT.
8. Задаем источники температуры в точках, в одной постоянный в другой нет:
M.M. => SOLUTION => –LOADS– APPLY => HEAT GENERAT => ON KEYPOINTS => выделяем точку №5 => OK=> BFK = NEW TABLE => OK=> NAME OF NEW TABLE = IT => I, J, K = 2, 1, 1 соответственно. В соответствии с рисунком 35 заполняем поля таблицы 1 и потом: FILE => APPLY/QUIT. Далее повторяем операцию: M.M. => SOLUTION => –LOADS– APPLY => HEAT GENERAT => ON KEYPOINTS => выделим точку №6 => OK => BFK = CONSTANT VALUE, VALUE = 10E6 => OK.
9. Определим начальную температуру пластины:
M.M. => SOLUTION=> –LOADS– APPLY => INITIAL CONDIT’N => DEFINE => PICK ALL => LAB = TEMP, VALUE = 20 => OK.
10. Задаем параметры расчета:
M.M. => SOLUTION => –ANALYSIS TYPE– Sol’s Control => Закладка BASIC => Time at end of loadstep = 10; Number of substeps = 50; Закладка Transient => Ramped Loading => OK.
11. Расчет:
M.M. => SOLUTION => –SOLVE– CURRENT LS => OK.
12. Просматриваем результаты расчета:
В районе переменного источника тепла выделяем узел и строим график температуры, выделенного узла, в зависимости от времени при помощи команд:
|
|
M.M. => TIMEHIST POSTPRO => DEFINE VARIABLES => ADD => NODAL DOF RESULT => ОК и M.M. => TIMEHIST POSTPRO => GRAPH VARIABLES….
Выводим поле температур в момент времени, когда температура ранее выделенного узла максимальна при помощи команд:
M.M. => GENERAL POSTPROC => –READ RESULTS– BY TIME/FREQ… и M.M. => GENERAL POSTPROC => PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU => DOF SOLUTION => OK.
Содержание отчета: краткие теоретические сведения, подробное описание всех шагов расчета с помощью ANSYS при решении нестационарной тепловой задачи, рисунки состояния детали после приложения нагрузок. Выводы.