Лабораторная работа №9
Цель и задачи работы
1.1. Изучить явление интерференции света и метод определения кривизны линзы с помощью интерференционных полос равной толщины.
1.2. Определить радиус кривизны линзы.
Теория.
Интерференция световых волн. Когерентность волн.
Интерференцией света называется наложение двух или более волн, при котором происходит пространственное перераспределение интенсивности света, наблюдаемое в виде темных и светлых полос.
Возникновение интерференции связано, во-первых, с тем, что для векторов напряженности электрических полей, описывающих электромагнитные волны, выполняется принцип суперпозиции. Так при наложении двух волн, каждая из которых создает в точке наблюдения соответственно электрические поля напряженностью E1 и E2, результирующая напряженность в точке наложения будет равна:
Ep = E1 + E2 (1)
Во-вторых, возникновение интерференции связано с тем, что все регистрирующие приборы, в том числе и человеческий глаз, регистрируют не величину напряженности электрического поля, а величину усредненного по времени потока энергии волны, которая характеризуется интенсивностью света (I), равной квадрату амплитуды напряженности электрического поля волны E0:
I = E02 (2)
При наложении нескольких волн интерференция наблюдается далеко не в каждом случае. Термин когерентность волн характеризует способность волн при наложении интерферировать. Волны называются когерентными, если при их наложении возникает интерференционная картина и некогерентными, если при их наложении интенсивности волн суммируются и интерференционная картина не возникает. Волны когерентны, если разность фаз между ними остается постоянной во время наблюдения. Для некогерентных волн разность фаз между ними хаотически изменяется во времени.
|
|
Рассмотрим наложение двух световых волн, идущих от двух источников S1 и S2, в точку Р (см.рис.1). Волны будем полагать монохроматическими и плоскими. Тогда выражения для напряженностей электрического поля двух волн можно записать в виде:
E1 = E10 cos(ωt – kz), E2 = E20cos(ω1t – k1z1) (3)
где Е10 и Е20 - амплитуды первой и второй волн,
ω и ω1 - циклические частоты первой и второй волн,
k и k1 - волновые числа первой и второй волн (k = 2π/λ, здесь λ -длина волны),
z и z1 - расстояния пройденные волнами от источников до точки наблюдения, t - время в момент наложения волн.

Рис.1- Схема двухлучевой интерференции.
Обозначив фазы двух волн, т.е. аргументы периодической функции (в данном случае косинуса), описывающей волны, через φ и φ 1 соответственно, можно записать, что разность фаз двух волн равна:
∆φ = φ – φ1 = (ω – ω1)t – kz + k1 z1 (4)
Из этого выражения видно, что условие когерентности, т.е. постоянство разности фаз во времени, может выполняться лишь для волн с одинаковыми частотами (ω = ω1).
Так как циклическая частота однозначно связана с волновым числом k = ω/v, (где v - фазовая скорость света в среде - величина постоянная, зависящая только от показателя преломления среды) волновые числа (длины волн) для когерентных волн, распространяющихся в одной среде, также должны быть одинаковыми, и в этом случае для когерентных волн разность фаз определяется геометрической разностью хода волн от источников до точки наложения волн (∆):
|
|
∆φ = k (z – z1) = k ∆. (5)
Для того чтобы учесть изменение волнового числа, а соответственно и длины волны, при переходе из одной среды в другую (частота при этом не изменяется) вместо геометрической разности хода удобнее использовать понятие оптическая разность хода волн.
Волновое число в среде (kc) пропорционально показателю преломления среды:
kc = k n, (6)
где k - волновое число в вакууме.
Чтобы не рассчитывать волновое число (длину волны) в различных средах, обычно используют значение волнового числа в вакууме, а разность фаз двух волн находят как произведение волнового числа в вакууме (это значение практически равно значению волнового числа в воздухе) на оптическую разность хода (∆), т.е. разность оптических длин путей двух волн (L 01 и L02 ):
∆φ = k (Lo1- Lo2) = k ∆. (7)
Оптическая длина пути волны, прошедшей несколько различных сред (см. рис.2), находится как сумма произведений показателя преломления среды (n 1) на геометрическое расстояние, пройденное волной в данной среде (z1):
L0 = n1 z1 + n2 z2 + n3 z3 +... + n1 z1 +... (8)

Рис.2. Оптическая длина пути волны, идущей из точки S в точку Р через различные среды.
Оптической длиной пути световой волны называется произведение геометрической длины пути (z1) световой волны в среде на абсолютный показатель преломления (n1) данной среды: Loпт = zi · ni
2.2. Двухлучевая интерференция
Пусть световые волны, испускаемые источниками S1 и S2, являются монохроматическими с одинаковой и постоянной частотой ω, а в рассматриваемой точке наблюдения Р (см.рис.1) оба вектора E1 и E2 параллельны друг другу, тогда их можно считать скалярными величинами и записать результирующую напряженность электрического поля в точке Р в соответствии с принципом суперпозиции (1) в следующем виде:
|
|
Ер = Е10 cos (ωt – kz1) + E20cos (ωt – kz2) (9)
Для сложения двух гармонических функций удобно пользоваться методом фазовых диаграмм. При этом напряженность электрического поля волны представляется как проекция на некоторую ось 00 ' вектора по величине равного амплитуде волны, повернутого относительно этой оси на угол равный фазе волны (см. рис. За).
Если координата точки наблюдения и положение источника неизменны, то во время наблюдения расстояние z постоянно, и фаза волны будет зависеть только от времени. С течением времени фаза волны будет расти и вектор Е0 будет вращаться с частотой ω относительно выбранной оси. Проекция вектора при этом будет изменяться по гармоническому закону в соответствии с уравнением:
E(t) = Eo cos (ωt + φ) (10)
где φ - начальная фаза волны, зависящая от z.

Рис.3. Фазовые диаграммы одной волны - (а) и двух - (в), налагающихся волн.
При сложении двух волн, каждая из них представляется проекцией соответствующего вектора на выбранную ось, и результирующая волна равна сумме проекций (см. рис.Зв). Результат не изменится, если сначала сложить вектора, а затем взять проекцию.
Так как для нахождения интенсивности достаточно знать амплитуду результирующей волны (см. формулу 2), то после сложения векторов можно и не искать проекцию результирующего вектора на ось, а ограничится найденой амплитудой результирующей волны (Ер0) и определить интенсивность света в точке наложения.
Из рис. Зв видно, что амплитуда результирующего вектора не зависит от фаз налагающихся волн (фазы волн изменяются с течением времени, что приводит к синхронному вращению векторов), а зависит лишь от разности фаз (∆φ) между налагающимися волнами (на рисунке разность фаз - это угол между векторами Е10 и E20) и от амплитуд этих волн.
Применяя теорему косинусов (см. рис.Зв), можно записать:
Еp02 = Е102 + E202 + 2E10 E20 cos ∆φ (11)
Так как интенсивность света (I) пропорциональна квадрату амплитуды колебаний вектора напряжённости электрического поля, то
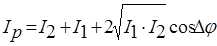
 (12)
(12)
Последнее слагаемое называют интерференционным членом. В тех
точках пространства, для которых cos ∆φ > 0, результирующая интенсивность (Ip) будет превышать сумму интенсивностей I1 и I2. В точках, для которых cos ∆φ < 0, Ip будет меньше I1 + I2.
Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других - минимумы интенсивности.
При измерении результирующей интенсивности света в точке наблюдения, может быть два крайних случая в зависимости от разности фаз (∆φ). Из (12) следует:
1).Результирующая интенсивности - I p при наложении двух когерентных волн максимальна
 , если ∆φ = 2πm. (13)
, если ∆φ = 2πm. (13)
Сравнивая (7) и (13), можно сказать, что при интерференции наблюдается максимум интенсивности, если оптическая разность хода двух интерферирующих волн равна целому числу длин волн
∆ = т λ (14)
где m - называется порядком интерференции и показывает, сколько длин волн укладывается в оптической разности хода (m = 0, ±1, ±2,...).
2).Результирующая интенсивность I - минимальна.
 , если ∆φ = (2m +l) π, (15)
, если ∆φ = (2m +l) π, (15)
где - m = 0, ±1, ±2,...
Т.е. минимум интенсивности наблюдается, если оптическая разность хода равна нечетному числу полуволн:
∆ = (2m +1) λ/2. (16)
Особенно отчётливо интерференция проявляется в том случае, когда I1 = I2. В этом случае в максимумах Ip = 4 I1, а в минимумах Ip = 0.
Интерференционная картина при наложении монохроматических волн состоит из чередующихся максимумов и минимумов света, обычно наблюдаемых в виде чередующихся светлых и тёмных полос. В случае интерференции белого света полосы окрашены, т.к. условия максимума и минимума интенсивности зависят от λ (см. формулы 14,16).
Для некогерентных волн ∆φ непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее значение cos ∆φ равно нулю, и всюду получается одинаковая результирующая интенсивность Iр = 2I1.