При освещении тонкой плёнки или пластинки происходит наложение световых волн, отразившихся от передней и задней поверхностей плёнки. Эти две волны получаются делением волны, идущей от одного источника S (см. рис.4). Для плоскопараллельной пластинки постоянной толщины интерференционная картина наблюдается в фокальной плоскости линзы, собирающей отражённые от верхней и нижней граней пластинки пучки лучей 1 и 2.
Лучи 1 и 2 образуются из падающего на пластинку луча SA. От источника S до точки А между ними разность хода отсутствует. Линия DC, перпендикулярная лучам 1 и 2, представляетсобой волновую поверхность, т.е. поверхность постоянной фазы.
Линза не вносит дополнительной разности хода для параллельных лучей, а лишь преобразует плоскую волну в сходящуюся сферическую волну. Поэтому после перпендикуляра DC, опущенного на лучи 1 и 2, до точки наложения лучей Р разность хода между лучами 1 и 2 также не возникает.
 |
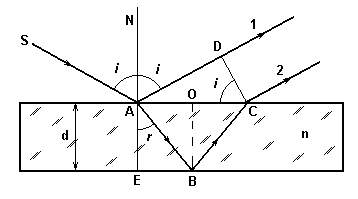Рис.4. Интерференция света в тонкой пленке.
Оптическая разность хода между лучами 1 и 2 возникает из-за того, что первый луч прошел, отразившись от границы раздела воздух-среда, отрезок AD в воздухе, а второй луч прошел путь АВС от точки А до точки С в пластинке с показателем преломления n и отразился от границы раздела среда-воздух.
При отражении световой волны от оптически более плотной среды (отражение луча 1 в точке А) фаза отраженной волны изменяется на противоположную (т.е. на π). Это можно представить как возникновение разности хода равной половине длины волны для первого луча. При отражении волны от оптически менее плотной среды (отражение луча 2 в точке В) изменения фазы не происходит, и соответственно разности хода не возникает.
|
|
Поэтому колебания в точку С (волновая поверхность DC) приходят оптическими путями: L1 = n(AB + ВС) и L2 = AD + λ/2. Отсюда можно записать, что оптическая разность хода, возникающая между лучами 1 и 2 от источника S до точки наложения лучей Р будет равна:
∆ = L 1 - L2 = n (АВ + ВС) - (AD + λ /2) = 2nАВ - AD – λ /2 (19)
Отрезки AD и АВ удобнее выразить через толщину пластинки (d) и угол падения луча (i) или угол преломления луча (r), используя треугольники ABE и ACD:
из треугольника ABE АВ = d / cos r, ЕВ = d tg r (20)
из треугольника ADC AD = AC sin i, AC = 2EB = 2d tg r,
∆ = 2nd/Cos r – AC Sin i = 2nd /Cos r - 2dtg rsin i = 2nd / Cos r - 2dSin r /Cos r Sin i = 2d/Cos r (n - Sin r Sin i)
по закону преломления света на границе двух сред Sin i = n Sin r, тогда
Δ = 2d/Cos r (n - nSin2r), умножим левую половину равенства на n\n
Δ= 2d/nCos r.(n2 - n2 Sin2r),из тригонометрии знаем, что 
,
тогда, если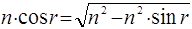 
то получим:
(21)
вспомним, что n · Sin r = Sin i, тогда 
, учтём изменение фазы отражённого луча на λ⁄2 и получим:
(22)
2.5.Вывод рабочей формулы определения радиуса кривизны линзы
Интерференционные полосы равной толщины в тонкой пленке, т.е. темные или светлые полосы соответствующие постоянному значению толщины пленки (d), можно наблюдать в воздушной прослойке между соприкасающимися друг с другом плоской поверхностью пластинки и выпуклой сферической поверхностью линзы (см. рис.5).
При этом толщина воздушной прослойки постепенно увеличивается от центра линзы к ее краям. При нормальном (перпендикулярном поверхности) падении света полосы равной толщины имеют вид концентрических окружностей, которые получили название колец Ньютона.
|
|
Если на линзу падает пучок монохроматического света, то световые волны, отражённые от верхней и нижней границ воздушной прослойки, интерферируют между собой.
Так как, в отличии от выше приведённого примера, отражение световой волны происходит в точке В от раздела среды воздух-стекло, а не стекло-воздух, как на рис.4,то λ/2 добавляется к слагаемому L1 и формула (19), в начальной её части приобретёт вид:
∆ = L1- L2 = (АВ + ВС + λ/2) - AD = 2d + λ /2
То есть, оптическая разность хода, в этом случае равна удвоенной толщине воздушного зазора (2d) (показатель преломления воздуха n = 1).
В итоге получим:
∆ = 2d + λ/2. (23)
Рис.5. Схема возникновения Рис.6. Учет деформации
колец Ньютона линзы
Тёмные кольца образуются там, где оптическая разность хода равна нечётному числу полуволн (см.16):
∆ = 2d + λ /2 = (2m + 1) λ /2, (24)
т.е. при толщине зазора
d = m λ /2, (25)
где m = 0,1,2,3... - номер кольца.
Радиус m-ного темного кольца (rm) определяется из треугольника AОС (см.рис.5)
rm2 = R2 - (R - d,)2 = 2Rd – d 2, (26)
где R - радиус кривизны линзы. Полагая величину воздушного зазора в месте возникновения колец малой, (т.е. d «R) можно записать:
rm2 = 2Rd. (27)
Из этой формулы видно, что радиус кривизны линзы можно найти, измерив радиус кольца Ньютона и величину воздушного зазора в месте возникновения кольца. Радиус колец Ньютона можно измерить, воспользовавшись микроскопом, имеющим измерительную шкалу. Чтобы не измерять величину зазора (кстати, не понятно, как это сделать экспериментально), можно воспользоваться интерференционным условием возникновения темных колец (24).
|
|
Тогда радиус кривизны линзы можно выразить через радиус кольца Ньютона, длину волны используемого света и номер измеряемого кольца:
rm2 = Rmλ (28)
Использование формулы (28) для определения радиуса кривизны может привести к ошибке, т.к. в точке соприкосновения линзы и стеклянной пластинки возможна деформация линзы по величине сравнимая с длиной волны света, поэтому использование выводов, основанных на рис.5 (см. формулы 26,27,28), будет некорректным.
Экспериментально наблюдаемая величина воздушного зазора может быть меньше теоретической величины, полученной из рис.5 на величину деформации стеклянной пластинки и линзы (δ) (см. рис.6). Поэтому в реальном эксперименте в формулу (27) вместо толщины воздушного зазора (d) необходимо подставить сумму толщины воздушного зазора и величины деформации линзы и стеклянной пластинки (d + δ). Учитывая, что условие возникновения темного кольца (24) определяется лишь толщиной зазора, получим следующую формулу, связывающую радиусы колец Ньютона с радиусом кривизны линзы:
rm2 = Rmλ + 2Rδ (29)
Экспериментально удобнее вместо радиуса кольца Ньютона измерять его диаметр (Dm). В этом случае формула (29) будет иметь вид:
D m2 = 4Rmλ + 8Rδ, (30)
Из (30) видно, что квадрат диаметра кольца Ньютона (Dm2) пропорционален порядковому номеру кольца (m). Если построить график зависимости Dm2 = f(m), то экспериментальные точки должны лежать на одной прямой, и тангенс угла наклона этой прямой (α) будет равен 4Rλ. Таким образом, для нахождения радиуса кривизны линзы необходимо, используя график зависимости Dm2 = f(m), найти
, (31)
а затем рассчитать радиус кривизны линзы по формуле:
R=tgα/4λ (32)
Вследствие деформации в центре линзы наблюдается круглое темное пятно, соответствующее нулевой толщине воздушного зазора. Измерив диаметр центрального темного пятна (кольца Ньютона, номер которого m = 0), можно найти величину деформации линзы по формуле:
δ= D02/8R (33)
Описание установки (Рис.7 и 8) и методика выполнения работы.
Интерференционная картина наблюдается с помощью микроскопа.
Свет от источника 1, пройдя светофильтр 3, становится монохроматическим и попадает на линзу 8, помещенную на стеклянную пластинку 9.
Диаметры колец Ньютона измеряются с использованием микрометра в микроскопе ‘Эликон’ и по делениям шкалы окуляра в микроскопе МБС-9, иопределяются разницей чисел делений, приходящихся на левый и правый края измеряемого кольца.
3.1.1. Измерение диаметров колец микроскопом ‘Эликон’ (Рис.7).
В фокальной плоскости окуляра микроскопа расположены неподвижная шкала с делениями от 0 до 8 и подвижные перекрестие и индекс в виде биштриха..
При вращении микрометрического винта (барабана) перекрестие и биштрих перемещаются в поле зрения окуляра относительно неподвижной шкалы. При повороте барабана на один оборот, биштрих и перекрестие, в поле зрения окуляра, переместятся на одно деление шкалы.
Барабан по окружности разделён на 100 делений. Поворот барабана на 1 деление соответствует перемещению перекрестия на 0,01 деления неподвижной шкалы. Полный отсчёт по шкале окулярного микрометра складывается из отсчета по неподвижной шкале и отсчета по барабану
На Рис.7 биштрих находится между делениями "5" и "6" неподвижной шкалы, а микрометрический барабан находится, к примеру, на делении "35" (напротив неподвижного индекса).
Следовательно, полный отсчёт составляет: 500 + 35 = 535 делений. Диаметры колец определяются разницей чисел делений, приходящихся на левый и правый края измеряемого кольца.
Для перевода делений в мм необходимо ввести коэффициент К, учитывающий кратность увеличения микроскопа.
3.1.2 Измерение диаметров колец микроскопом МБС−9 (Рис.8).
В фокальной плоскости окуляра микроскопа расположены перекрестие и шкала с делениями от 0 до 18. Кольца Ньютона проецируются в центр перекрестия. Диаметры колец определяются разницей чисел делений, приходящихся на левый и правый края измеряемого кольца.
На Рис.8 правый край нулевого кольца находится на делении 105, а левый−на делении 75.
Для перевода делений в мм необходимо ввести коэффициент К, учитывающий кратность увеличения микроскопа.
 |
 |
Рис.7. Микроскоп “Эликон: 1−источник света, 2 – конденсор, 3 – светофильтр, 4 – полупрозрачное зеркало, 5 – объектив, 6 – окуляр, 7 – шкала.
Объект исследования: 8–линза,9–стеклянная пластина.
 |
 |
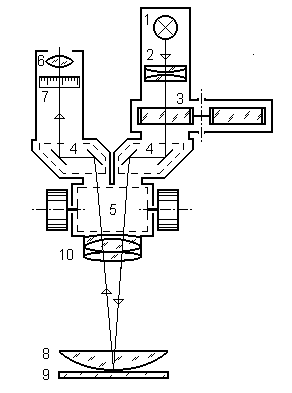Рис.8. Микроскоп МБС−9: 1−источник света, 2−конденсор, 3−светофильтр, 4 − призма, 5 – блок масштабирования, 6 – окуляр, 7 – шкала, 10−объектив.
Объект исследования: 8–линза, 9–стеклянная пластина.