ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Механика – раздел физики, изучающий механическое движение и взаимодействие материальных тел.

Основные разделы механики:

- кинематика (изучает движение тел без учёта сил, вызывающих эти движения),

- динамика (изучает закономерности движения тел, обусловленные действующими на них силами),

- статика (изучает законы равновесия тел).

 

Материальная точка - это тело, размерами и формой которого в условиях данной задачи можно пренебречь.

Механическим движением – называется перемещение тела в пространстве относительно других тел с течением времени.

Для описания движения материальной точки необходима система отчета.

Системой отсчета называется совокупность тела отсчета, системы координат и часов для измерения времени.

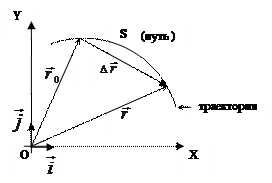
Траектория – это линия, по которой движется материальная точка.

Путь S – это длина траектории, по которой двигалась материальная точка.

Положение материальной точки в пространстве задается радиусом-вектором г.

Радиус – вектор 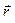– это вектор, проведённый из начала координат в рассматриваемую материальную точку.

, ,

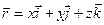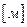где 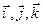— единичные векторы направлений (орты);

х, у, z — координаты точки.

Модуль радиус – вектора равен:

Перемещение – это вектор, направленный из начального положения материальной точки в её конечное положение: ,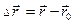

где и - это начальный и конечный радиус – вектор материальной точки. , метр

Поступательным называется движение, при котором любая прямая, проведённая в теле, остаётся параллельной сама себе при движении тела.

 

Основными особенностями такого вида движения являются следующие обстоятельства:

- при поступательном движении все точки тела движутся совершенно одинаково, то есть имеют одну и ту же скорость, ускорение, траектории движения, совершают одинаковые перемещения и проходят одинаковый путь.

- в этом случае при описании движения тела его можно рассматривать как материальную точку.

Для описания поступательного движения тел вводят в рассмотрение следующие понятия:

Для характеристики быстроты перемещения тела в пространстве вводят понятие скорос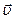ти :

, размерность скорости: 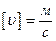, метр в секунду.

Мгновенная скорость , , где - проекции скорости v на

оси координат.

Модуль скорости тела равен:

Таким образом, мгновенной скоростью называется векторная величина, равная первой производной радиус-вектора тела по времени.

Физический смысл скорости: она показывает, какое перемещение совершает тело за единицу времени при равномерном движении.

(пример: означает, что тело за каждую секунду перемещается на 5 м.)

Вектор мгновенной скорости направлен по касательной к траектории движения материальной точки.

Для характеристики быстроты изменения скорости по величине и направлению вводят понятие ускоре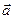ния :

, размерность ускорения: 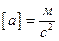, метр на секунду в квадрате.

Таким образом, ускорением называется векторная величина, равная первой производной мгновенной скорости тела по времени.

Мгновенное ускорение: , ,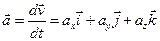

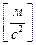где 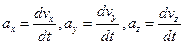- проекции ускорения на оси координат.

Модуль вектора ускорения равен: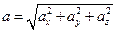

Физический смысл ускорения: оно показывает, на сколько изменяется скорость тела за единицу времени при равнопеременном движении.

(например: 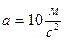означает, что скорость тела изменяется на 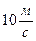за каждую секунду.)

Направление вектора ускорения 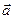совпадает с направлением вектора .

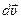При прямолинейном движении тела ускорение:

- сонаправлено с вектором в случае ускоренного движения тела

 

- противоположно направлено вектору при замедленном движении тела

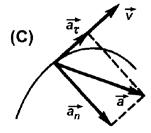При криволинейном движении вектор ускорения 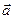в общем случае образует с вектором мгновенной скорости некоторый угол .

В этом случае вектор полного ускорения удобно разложить на две составляющие и ,

где 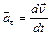- тангенциальное (или касательное) ускорение (характеризует быстроту изменения вектора скорости по величине),

- нормальное (или центростремительное) ускорение (характеризует быстроту изменения вектора скорости по направлению)

Из рис. следует, что и

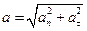
Вращательным называется движение, при котором все точки тела описываю окружности, центры которых лежат на одной и той же прямой, называемой осью вращения тела.

 

 

Основной особенностью такого вида движения является следующее обстоятельство:

при вращательном движении все точки тела движутся с одной и той же угловой скоростью и угловым ускорением и совершают одинаковые угловые перемещения.

 

 

Для описания вращательного движения тела вводят в рассмотрение следующие понятия:

Угол поворота 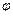- это угол, на который поворачивается радиус-вектор любой точки тела при его вращении.

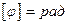, радиан.

Элементарное угловое перемещение 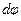можно рассматривать как вектор , направление которого определяется по правилу буравчика (правилу правого винта):

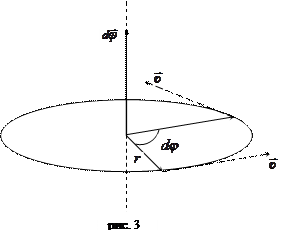
если рукоятку буравчика вращать по направлению вращения тела, то поступательное движение буравчика будет совпадать с направлением вектора (см. рис. 3).

 

 

Удобство такого введения в следующем:

- модуль вектора однозначно определяет величину элементарного поворотатела ,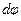

- направление вектора через правило буравчика определяет направление вращения тела,

- положение вектора в пространстве определяет ось вращения тела.

 

Для характеристики быстроты вращения тела в пространстве вводится понятие угловой скорости .

, размерность 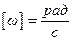, радиан в секунду.

Угловая скорость есть первая производная по времени от угла поворота.

Физический смысл угловой скорости: она показывает, на какой угол поворачивается радиус-вектор любой точки тела за единицу времени при равномерном вращении.

(например: 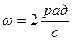означает, что за каждую секунду радиус-вектор поворачивается на 2 радиана)

Направление угловой скорости совпадает с направлением вектора , то есть она также определяется по правилу буравчика.

Для характеристики быстроты изменения угловой скорости вводится понятие углового ускорения :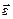

, размерность , радиан на секунду в квадрате.

Физический смысл углового ускорения: оно показывает, на сколько изменяется угловая скорость тела за единицу времени при равнопеременном вращении.

(например: 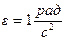означает, что за каждую секунду угловая скорость тела изменяется на .)

Направление вектора углового ускорения 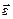совпадает с направлением вектора , то есть оно сонаправлено с вектором при ускоренном вращении тела и противоположно направлено при замедленном вращении.

Векторы, направление которых связывают с направлением вращения, называются псевдовекторами или аксиальными в отличие отобычных векторов (, , 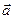и т.д.), которые называются полярными.

 

Период обращения Т – это время одного полного оборота.

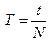, где t – время, за которое точка сделает N оборотов.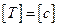

Частота обращения (частота вращения) n – это число оборотов за единицу времени.

, где N – число оборотов за время t.

Причём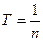

Равномерное движение материальной точки по окружности – это движение с ускорением, которое называется нормальным или центростремительным а_{ц с.} (оно характеризует быстроту поворота вектора скорости по направлению и направлено к центру окружности, по которой движется точка).