Лекции 17-18 Классы интегрируемых функций
Содержание лекции: Интегрирование основных классов функций: рациональных функций, тригонометрических функций.
Интегрирование иррациональных функций. «не берущиеся» интегралы.
Интегрирование рациональных функций
В предыдущей лекции мы познакомились с основными приемами вычисления неопределенного интеграла. Эти приемы не определяют точно пути, по которому следует идти, чтобы вычислить заданный интеграл, предоставляя многое искусству вычислителя.
Рассмотрим подробнее некоторые важнейшие классы функций и по отношению к их интегралам установим вполне определенный порядок вычислений.
Известны сравнительно немногие классы функций, для которых интегрирование может быть выполнено в конечном виде, т.е. первообразная может быть выражена через элементарные функции. Простейшим из таких классов является класс рациональных функций. Целые рациональные функции интегрируются просто – используя табличные формулы и свойство линейности. Поэтому рассмотрим интегрирование дробно-рациональных функций (рациональных дробей), т.е. функций вида
.
Из линейной алгебры известно, что всякую рациональную дробь можно разложить на сумму простейших дробей типа
I.  (А, а – константы)
|
II. 
, (k ³ 2 целое число)
III. 
(М, N, p, q – константы, дискриминант знаменателя меньше нуля)
IV. 
(k ³ 2 целое, знаменатель не имеет корней)
Интегрирование дробей I – III типов трудностей не представляет. Действительно,
I. 
,
II.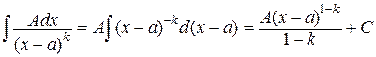 
,
III.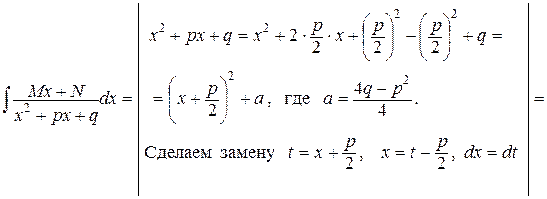 
.
Таким образом, интегрирование свелось к двум интегралам, один из которых - табличный:
,
а второй легко вычисляется подведением под знак дифференциала:
.
Интегралы IV типа требуют более сложных вычислений. Но и в этом случае выделение полного квадрата в знаменателе, а затем замена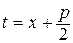 
дает возможность упрощения интеграла. В частности, интеграл вида 
можно вычислить, используя интегрирование по частям, а можно воспользоваться рекуррентными формулами, которые имеются в любом справочнике по высшей математике.
Таким образом, если заданную рациональную дробь разложить в сумму простейших, то интегрирование этой суммы уже не составит особого труда.
Пример 1.
Найти: а) 
; б) 
; в) 
; г)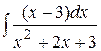 
Решение.
а) 
;
б) 
;
в) 
= 
;
г)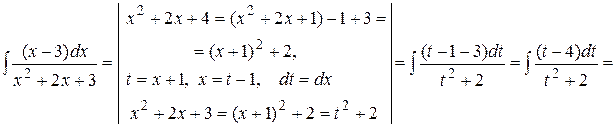 
.
Пример 2.
Найти 
Решение. Подынтегральная функция 
есть неправильная рациональная дробь. Сначала выделим целую часть этой дроби, для чего разделим числитель на знаменатель:
,
тогда = х – 1 + 
.
Рассмотрим правильную дробь и разложим ее на простейшие:
= 
.
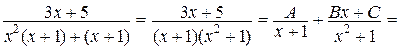
Сравнивая числители полученной и исходной дробей, находим
х 2 А + В = 0
х В + С = 3 Þ А = 1, В = –1, С
св.чл. А + С = 5.
Значит, = 
. Тогда, искомый интеграл равен
= 
= 
= 
.
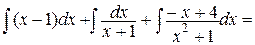
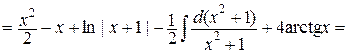
Интегрирование тригонометрических функций
Рассмотрим интегралы типа 
. С помощью подстановки 
такой интеграл всегда можно преобразовать в интеграл от рациональной дроби относительно переменной t. Действительно, т.к.
при 
, 
,
х = 2arctg t,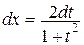 
,
то = 
– под знаком получившегося интеграла стоит рациональная функция, принцип интегрирования которой мы уже обсудили.
Подстановка называется универсальной, так как позволяет тригонометрическую функцию свести к рациональной, но иногда интегрирование получившейся рациональной дроби требует довольно сложных выкладок. Поэтому наряду с универсальной подстановкой рассматривают частные подстановки, которые в некоторых случаях упрощают вычисления.
Функцию R(u (x), v (x)) называют нечетной относительно функции и (х), если R(– u, v) = –R(u, v);
функция R(u (x), v (x)) называют нечетной относительно функции v (х), если R(u, – v) = –R(u, v);
функция R(u (x), v (x))– четная относительно и (х), если R(– u, v) = R(u, v);
функция R(u (x), v (x)) – четная относительно v (х), если R(u, – v) = R(u, v);
если R(– u, – v) = R(u, v), то функция R(u (x), v (x)) четная относительно обеих функций u и v.
А) Если в интеграле функция R (sin x, cos x) – нечетная относительно sin x, то ее можно представить в виде R 1(cos x)sin x, тогда используется подстановка cos x = t:
= 
.
Б) Если в интеграле функция R (sin x, cos x) – нечетная относительно cos x, то ее можно представить в виде R 1(sin x)cos x, тогда используется подстановка sin x = t:
= 
.
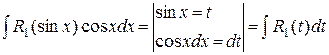В) Если в интеграле функция R (sin x, cos x) – четная относительно sin x и cos x, то она может быть преобразована к виду R 1(tg x) или R 2(сtg x), поэтому используется подстановка tg x = t или ctg x = t соответственно:
=
= 
.
Рассмотрим примеры.
Пример1.
1) Найти 
. Используем универсальную подстановку:
2) Найти 
. Заметим, что функция 
– нечетная относительно sin x. Действительно,
R (–sin x, cos x) =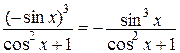 
= – R (sin x, cos x),
поэтому рациональнее применить не универсальную, а частную подстановку t = cos x:
.
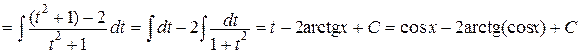3) Найти 
. В этом случае, подынтегральная функция четная относительно sin x и cos x:
,
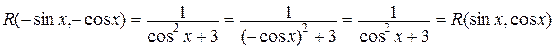поэтому удобно сделать подстановку t = tg x. Получим
.
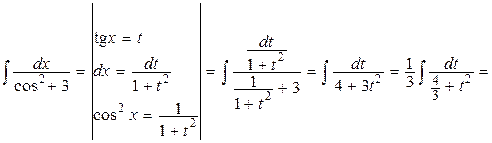
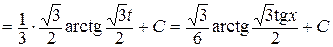Г) Рассмотрим интеграл вида 
Если п и т – четные, то для упрощения подынтегрального выражения используются формулы понижения степени:
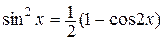
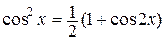
В остальных случаях возможных значений п и т могут быть использованы частные подстановки А), Б), В), а так же другие преобразования подынтегральной функции.
Д) Интегралы вида 
, 
, 
легко вычисляются в результате применения формул
Рассмотрим примеры.
Пример2.
1) 
2) 
.
3) 
.
Таким образом, интегрирование тригонометрических функций основано, по существу, на использовании тригонометрических тождеств для преобразования подынтегрального выражения.