В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние SAB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол αAB или румб rAB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.
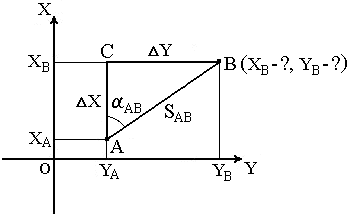
Рис. 23. Прямая геодезическая задача
Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.
Дано: Точка А(XA, YA), SAB и αAB.
Найти: точку В(XB, YB).
Непосредственно из рисунка имеем:
ΔX = XB – XA;
ΔY = YB – YA.
Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:
ΔX = SAB · cos αAB;
ΔY = SAB · sin αAB.
Так как в этих формулах SAB всегда число положительное, то знаки приращений координат ΔX и ΔY зависят от знаков cos αAB и sin αAB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1.
Таблица 1.
Знаки приращений координат ΔX и ΔY
| Приращения координат | Четверть окружности в которую направлена линия | |||
| I (СВ) | II (ЮВ) | III (ЮЗ) | IV (СЗ) | |
| ΔX | + | – | – | + |
| ΔY | + | + | – | – |
При помощи румба приращения координат вычисляют по формулам:
ΔX = SAB · cos rAB;
ΔY = SAB · sin rAB.
Знаки приращениям дают в зависимости от названия румба.
Вычислив приращения координат, находим искомые координаты другой точки:
XB = XA + ΔX;
YB = YA+ ΔY.
Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.
Обратная геодезическая задача заключается в том, что при известных координатах точек А (XA, YA) и В (XB, YB) необходимо найти длину SAB и направление линии АВ: румб rAB и дирекционный угол αAB (рис.24).

Даннная задача решается следующим образом.
Сначала находим приращения координат:
ΔX = XB – XA;
ΔY = YB – YA.
Величину угла rAB определем из отношения
| ΔY | = tg rAB |
| ΔX |
.
По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим αAB.
Для контроля расстояние SAB дважды вычисляют по формулам:
| SAB= | ΔX | = | ΔY | = ΔX · sec αAB = ΔY · cosec αAB |
| cos αAB | sin αAB |
| SAB= | ΔX | = | ΔY | = ΔX · sec rAB = ΔY · cosec rAB |
| cos rAB | sin rAB |
Расстояние SAB можно определить также по формуле
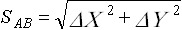 .
.
Высотная съемочная сеть
Высотная геодезическая сеть (нивелирная сеть) — сеть пунктов земной поверхности, высоты которых над уровнем моря определены геодезическим методом нивелирования. Пункты нивелирной сети закрепляют на местности нивелирными марками и реперами, которые закладывают в стены долговечных сооружений или непосредственно в грунт на некоторую глубину. Нивелирная сеть служит высотной основой топографических съемок, а при повторных определениях нивелирных высот её пунктов используется также для изучения вертикальных движений земной коры. Высотная опорная геодезическая сеть развивается в виде сетей нивелирования I-IV классов точности, а также технического нивелирования в зависимости от площади и характера объекта строительства. Исходными для развития высотной опорной геодезической сети являются пункты государственной нивелирной сети (ГНС).