ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
При исследовании эволюции экономических систем эффективными являются модели, где независимой переменной является время t. В таких моделях применяется аппарат теории дифференциальных уравнений.
Определение 1. Уравнение, содержащее независимую переменную x, неизвестную функцию у и ее производные называется дифференциальным уравнением:
или 
Определение 2. Порядок “старшей” производной называется порядком дифференциального уравнения.
Решить дифференциальное уравнение – это значит, определить функцию 
, удовлетворяющее этому уравнению.
Простейшее дифференциальное уравнение вида 
мы уже решали, так как находили 
. Мы знаем, что интеграл определяется с точностью до произвольного постоянного слагаемого. То есть решение простейшего дифференциального уравнения содержит произвольную постоянную. Решения более сложных дифференциальных уравнений также находятся с точностью до произвольных постоянных (возможно, нескольких). Конкретная функция, удовлетворяющая заданному уравнению, называется его частным решением. Решение, содержащее всевозможные произвольные постоянные, называется общим решением.
Число произвольных постоянных в общем решении равно порядку дифференциального уравнения.
Пример 1. 
Представим 
Тогда 
или
Отсюда
Интегрируя, получим:
Общее решение: 
Дифференциальное уравнение первого порядка
С разделяющимися переменными
Так называются уравнения вида 
. Запишем производную в виде отношения дифференциалов: 
и разнесем в разные части выражения, содержащие 
и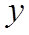 
. Мы получим равенство двух дифференциалов: 
. После интегрирования правой части по 
, а левой – по 
мы получим слева функцию, зависящую от 
, а справа – функцию, зависящую от , отличающиеся на константу: 
.
Пример 2.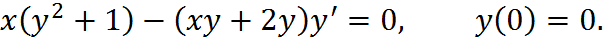 
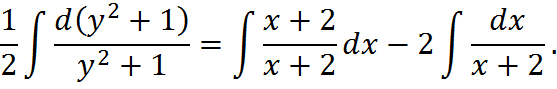
Подставим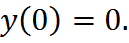 
Отсюда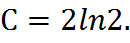 
Подставим в общее решение:
Демографическая задача. Модель Мальтуса
Пусть в момент времени t численность населения (или популяции биологическихобъектов: бактерий, вирусов, диких животных) составляет N (t),
а в некоторый фиксированный момент времени t 0 составляет N 0, причем N 0 – известная величина. Необходимо определить закон изменения во времени численности населения.
Производная 
– скорость изменения численности населения N (t). Если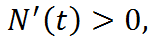 
то N (t) возрастает, а если 
то N (t) убывает. Так как
скорость изменения численности населения пропорциональна самой численности населения N (t), то динамика численности населения описывается
дифференциальным уравнением
(1)
где 
= const – параметр, определяемый разностью между рождаемостью и смертностью. Преобразуем уравнение (1).
= 
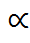или 
= 
Отсюда 
.
Интегрируя, получим: 
. Тогда общее решение уравнения (1) запишется в виде:
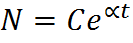. (2)
Так как при t =t 0 N = N 0, то из (2) следует 
. Поэтому окончательно получаем:
(3)
Найденное решение описывает закономерности изменения численности популяции, радиоактивного распада, процесса размножения бактерий, вирусов и т.д.
Актуальность демографической задачи для экономики заключается в том, что ее решение в масштабах региона или целого государства позволяет определять приток трудовых ресурсов в будущем.