Задача 1.
В баллон объемом 0,22  компрессором нагнетается газ СО2. Перед нагнетанием в баллоне было разрежение 200 мм. рт. ст., приведенное к нормальным условиям и температура 23
компрессором нагнетается газ СО2. Перед нагнетанием в баллоне было разрежение 200 мм. рт. ст., приведенное к нормальным условиям и температура 23 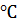 . После нагнетания газа в баллоне установилось избыточное давление 30 МПа, при температуре 37
. После нагнетания газа в баллоне установилось избыточное давление 30 МПа, при температуре 37 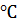 . Определить массу поданного в баллон газа, если барометрическое давление окружающего воздуха составляет
. Определить массу поданного в баллон газа, если барометрическое давление окружающего воздуха составляет 
Из уравнения состояния p * V = m * R * T имеем m =  .
.
Масса газа, находящаяся в баллоне до нагнетания
m 1 = 
где:  =
=  -
-  , R =
, R =  =
=  = 188,9 Дж/кг
= 188,9 Дж/кг  К, V = 0,22
К, V = 0,22  ,
,
Т = t1 + 273,15 = 23 + 273,15 = 296,15 К.
760 мм.рт.ст.=  =101,323кПа; 200 мм.рт.ст. =
=101,323кПа; 200 мм.рт.ст. =  = 26,664 кПа.
= 26,664 кПа.
 = 101,323 – 26,664 = 74,659 кПа = 74,659 *
= 101,323 – 26,664 = 74,659 кПа = 74,659 *  Па.
Па.
Тогда масса газа, находящаяся в баллоне до нагнетания
m 1 =  = 0,2936 кг.
= 0,2936 кг.
Масса газа, находящаяся в баллоне после нагнетания
m 2 = 
где:  =
=  -
-  , R = 188,9 Дж/(кг
, R = 188,9 Дж/(кг  К), V = 0,22
К), V = 0,22  ,
,
Т = t2 + 273,15 = 37 + 273,15 = 310,15 К.
 = 30 МПа + 101,323 кПа = 30101,323 кПа = 30101,323 *
= 30 МПа + 101,323 кПа = 30101,323 кПа = 30101,323 *  Па.
Па.
Тогда масса газа, находящаяся в баллоне до нагнетания
m 1 =  = 118,4 кг.
= 118,4 кг.
Масса поданного в баллон газа
m = m2 - m1 = 118,4 – 0,2936 = 118,1 кг.
Ответ: Масса поданного в баллон газа 118,1 кг.
Задача 2.
Для газовой смеси (генераторный газ), заданной объемными долями компонентов:  = 11%,
= 11%,  = 55%,
= 55%,  = 27%,
= 27%,  = 7%, и имеющей начальную температуру
= 7%, и имеющей начальную температуру  = 900
= 900  а конечную после процесса
а конечную после процесса  = 200
= 200 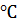 , определить:
, определить:
1) молекулярную массу и газовую постоянную смеси;
2) удельный объем и плотность смеси при нормальных условиях;
3) состав смеси в массовых долях;
4) количество теплоты, отданное 1 кг смеси при изобарном охлаждении ее от  до
до  ;
;
5) удельную истинную изобарную теплоемкость газовой смеси при  = 900
= 900 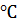 .
.
Молекулярная масса смеси
 =
=  *
*  +
+  *
*  +
+  *
*  +
+  *
* 
Молекулярные массы компонентов смеси
 = 44 кг/кмоль;
= 44 кг/кмоль;  = 28,03 кг/кмоль;
= 28,03 кг/кмоль; 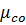 = 28,01 кг/кмоль;
= 28,01 кг/кмоль;
 = 2,016 кг/кмоль.
= 2,016 кг/кмоль.
Тогда молекулярная масса смеси
 = 0,11*44 + 0,55*28,03 + 0,27*28,01 + 0,07*2,016 = 27,96 кг/кмоль.
= 0,11*44 + 0,55*28,03 + 0,27*28,01 + 0,07*2,016 = 27,96 кг/кмоль.
Газовая постоянная
 =
=  =
=  = 297,35 Дж/кмоль
= 297,35 Дж/кмоль  К.
К.
Плотность смеси при нормальных условиях (рн = 760 мм.рт.ст. = 101,323 кПа; tн = 0 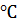 ).
).
 =
=  *
*  +
+  *
*  +
+  *
*  +
+  *
* 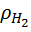
Плотность компонентов смеси
 = 1,977 кг/м3;
= 1,977 кг/м3;  = 1,251 кг/м3;
= 1,251 кг/м3;  = 1,25 кг/м3;
= 1,25 кг/м3;
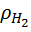 = 0,09 кг/м3;
= 0,09 кг/м3;
Плотность смеси при нормальных условиях
 = 0,11*1,977 + 0,55*1,251 + 0,27*1,25 + 0,07*0,09 = 1,24932 кг/м3;
= 0,11*1,977 + 0,55*1,251 + 0,27*1,25 + 0,07*0,09 = 1,24932 кг/м3;
Удельный объем – величина, обратная плотности
 =
=  =
=  = 0,8 м3/кг.
= 0,8 м3/кг.
Массовые доли компонентов смеси:  =
= 
 =
=  =
=  = 17,31%;
= 17,31%;  =
=  =
=  = 55,138%;
= 55,138%;
 =
=  =
=  = 27%;
= 27%;  =
=  =
=  = 0,5%.
= 0,5%.
Проверку:  +
+  +
+  +
+  = 100%.
= 100%.
Количество теплоты отводимое 1 кг смеси при изобарном охлаждении от  = 900
= 900 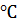 до
до  = 200
= 200 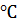 :
:
q = 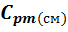 * (
* (  -
-  )
)
где:  – средняя массовая изобарная теплоемкость смеси в
– средняя массовая изобарная теплоемкость смеси в
интервале температур от  до
до  .
.
Массовые изобарные теплоемкости компонентов смеси при температурах:
1)  = 900
= 900 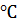 :
:  = 1,1045
= 1,1045 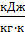 ;
;  = 1,1078
= 1,1078 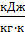 ;
;
 = 1,12
= 1,12 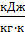 ;
;  = 14,706
= 14,706 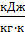 ;
;
1)  = 200
= 200 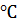 :
:  = 0,9487
= 0,9487 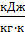 ;
;  = 1,0434
= 1,0434 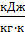 ;
;
 = 1,0463
= 1,0463 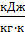 ;
;  = 14,421
= 14,421 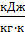 ;
;
Средние массовые изобарные теплоемкости смеси в заданном интервале температур:
 ;
;
 = 1,148
= 1,148 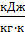 ;
;
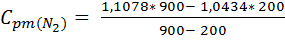 = 1,126
= 1,126 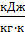 ;
;
 = 1,141
= 1,141 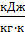 ;
;
 = 14,78
= 14,78 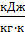 ;
;

 0,18*1,148+0,57*1,126+0,248*1,141+0,0014*14,78 = 1,152
0,18*1,148+0,57*1,126+0,248*1,141+0,0014*14,78 = 1,152 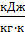
Количество теплоты: q = 1,152 * (200 – 900) = - 806,4 кДж – знак «-», значит теплота отводится.
Удельная истинная изобарная теплоемкость смеси при  = 200
= 200 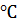 :
:

 0,18*0,9487+0,57*1,0434+0,248*1,0463+0,0014*14,421=1,045
0,18*0,9487+0,57*1,0434+0,248*1,0463+0,0014*14,421=1,045 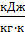
Задача 3.
Определить изменения внутренней энергии и энтальпии газа в интервале от  = 303
= 303 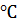 (
( = 576,15 К) до
= 576,15 К) до  = 576
= 576 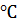 (
( = 849,15 К), если известны эмпирические (интерполяционные) формулы для определения теплоемкостей рассматриваемого газа. До подвода теплоты газ занимал объем V = 0,22
= 849,15 К), если известны эмпирические (интерполяционные) формулы для определения теплоемкостей рассматриваемого газа. До подвода теплоты газ занимал объем V = 0,22  и имел избыточное давление
и имел избыточное давление  = 0,3 МПа. Задачу решить двумя способами: с помощью удельной объемной и мольной теплоемкостей. Газ – азот (
= 0,3 МПа. Задачу решить двумя способами: с помощью удельной объемной и мольной теплоемкостей. Газ – азот ( ). Газовая постоянная R = 296,9
). Газовая постоянная R = 296,9  .
.
Абсолютное давление газа  =
=  +
+  = 0,3 + 0,1 = 0,4 МПа.
= 0,3 + 0,1 = 0,4 МПа.
Массу газа определим, использую давление состояния p * V = m * R * T:
m =  =
=  = 0,514 кг.
= 0,514 кг.
Объем газа при нормальных условиях (давление 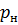 = 0,1 МПа, температура
= 0,1 МПа, температура  = 273,15 К):
= 273,15 К):
 0,417
0,417  .
.
Количество молей газа в объеме 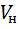 :
:
N =  = 0,017 кмоль.
= 0,017 кмоль.
где: 22,4  – объем, занимаемый 1 кмоль газа, для всех идеальных
– объем, занимаемый 1 кмоль газа, для всех идеальных
газов величина постоянная.
Интерполяционные формулы для определения теплоемкостей.
Средние объемные теплоемкости:
При V = const:  = 0,9123 + 0,00010492 (
= 0,9123 + 0,00010492 ( ) = 0,9123 + 0,00010492 * (303 + 576) = 1
) = 0,9123 + 0,00010492 * (303 + 576) = 1  .
.
При p = const:  = 1,2833 + 0,00010492 (
= 1,2833 + 0,00010492 ( ) = 1,2833 + 0,00010492 * (303 + 576) = 1,375
) = 1,2833 + 0,00010492 * (303 + 576) = 1,375  .
.
Средние мольные теплоемкости:
При V = const:  = 20,47 + 0,001117 (
= 20,47 + 0,001117 ( ) = 20,47 + 0,001117 (303 +576) = 21,45
) = 20,47 + 0,001117 (303 +576) = 21,45  .
.
При p = const:  = 28,78 + 0,00117 (
= 28,78 + 0,00117 ( ) = 28,78 + 0,00117 (303 +576) = 29,08
) = 28,78 + 0,00117 (303 +576) = 29,08  .
.
Изменение внутренней энергии и энтальпии:
- при использовании объемных теплоемкостей:
 = 0,417 * 1 * (576 – 303) = 113,841 кДж.
= 0,417 * 1 * (576 – 303) = 113,841 кДж.
 = 0,417 * 1,375 * (576 – 303) = 156,53 кДж.
= 0,417 * 1,375 * (576 – 303) = 156,53 кДж.
- при использовании мольных теплоемкостей:
 = 0,017 * 21,45 * (586 – 313) = 99,5кДж.
= 0,017 * 21,45 * (586 – 313) = 99,5кДж.
 = 0,017 * 29,08 * (586 – 313) = 134,96 кДж.
= 0,017 * 29,08 * (586 – 313) = 134,96 кДж.
Задача 4.
Газ в количестве 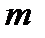 = 9 кг, имеющий начальную температуру
= 9 кг, имеющий начальную температуру  = 17
= 17 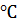 (
( = 290,15 К), расширяется при давлении
= 290,15 К), расширяется при давлении  = 3,4 МПа до двойного объема, а затем нагревается при
= 3,4 МПа до двойного объема, а затем нагревается при 
 . Определить работу и изменение энтропии за весь процесс (1 - 2 - 3), если после нагревания газ имеет давление
. Определить работу и изменение энтропии за весь процесс (1 - 2 - 3), если после нагревания газ имеет давление 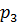 = 4,4 МПа. Представить процесс в
= 4,4 МПа. Представить процесс в  и
и  - диаграммах. Газ –
- диаграммах. Газ –  : газовая постоянная R = 259,8
: газовая постоянная R = 259,8  , молекулярная масса μ = 32 кг/кмоль. Теплоемкость принять не зависящей от температуры.
, молекулярная масса μ = 32 кг/кмоль. Теплоемкость принять не зависящей от температуры.
Кислород – двухатомный газ.
Мольные теплоемкости двухатомного газа:
при V = const -  = 20,9
= 20,9  , при p = const -
, при p = const -  = 29,3
= 29,3 
Массовые теплоемкости кислорода:
- изохорная  =
=  =
=  = 0,653
= 0,653 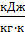
- изобарная  =
=  =
=  = 0,9156
= 0,9156 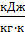
Параметры газа в характерных точках процессов.
Точка 1. – начало изобарного процесса 1 – 2: давление  = 3,4 МПа, температура
= 3,4 МПа, температура  = 290,15 К, объем из уравнения p*V = m*R*T:
= 290,15 К, объем из уравнения p*V = m*R*T: 
 =
=  = 0,1995
= 0,1995 
Точка 2. – конец изобарного процесса 1–2 и начало изохорного процесса 2–3:
объем  = 2 *
= 2 *  = 2 * 0,1995 = 0,399
= 2 * 0,1995 = 0,399  , давление
, давление  =
=  = 3,4 МПа, температуру определим, используя зависимость между параметрами в изобарном процессе
= 3,4 МПа, температуру определим, используя зависимость между параметрами в изобарном процессе  откуда
откуда  =
=  =
=  = 580 К.
= 580 К.
Точка 3. – конец изохорного процесса 2 – 3: давление 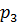 = 4,4 МПа, объем
= 4,4 МПа, объем  = 0,399
= 0,399  , из зависимости между параметрами в изохорном процессе
, из зависимости между параметрами в изохорном процессе 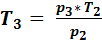 =
=  = 750,588 К.
= 750,588 К.
Работа за процесс 1 – 2 – 3:  =
=  +
+  .
.
Работа в изобарном процессе:  =
=  * (
* ( ) = 3,4 *
) = 3,4 *  * (0,399 – 0,1995) = 1356,6 кДж.
* (0,399 – 0,1995) = 1356,6 кДж.
В изохорном процессе работа равна нулю:  = 0.
= 0.
Работа за процесс 1 – 2 – 3:  = 1356,6 + 0 = 1356,6 кДж.
= 1356,6 + 0 = 1356,6 кДж.
Изменение энтропии:
- в процессе 1 – 2:  =
=  * ln
* ln  = 0,9156 * ln
= 0,9156 * ln  = 0.635
= 0.635 
- в процессе 2 – 3:  =
=  * ln
* ln  =0,653 * ln
=0,653 * ln  = 0.168
= 0.168 
- за процесс 1 – 3: ( +
+  ) * m = (0.635 + 0.168) * 9 = 7.227
) * m = (0.635 + 0.168) * 9 = 7.227 
Процессы на диаграммах в  - и
- и  - координатах
- координатах 

Задача 5.
Газ, имеющий начальные параметры - абсолютное давление  = 0,1 МПа и температуру
= 0,1 МПа и температуру  [
[  = 300,15 К] - сжимают до объема
= 300,15 К] - сжимают до объема  . Определить: работу за процесс сжатия, количество отведенной (или подведенной) теплоты, изменение внутренней энергии, энтальпии и энтропии газа за процесс, если количество газа m = 28 кг.
. Определить: работу за процесс сжатия, количество отведенной (или подведенной) теплоты, изменение внутренней энергии, энтальпии и энтропии газа за процесс, если количество газа m = 28 кг.
Задачу решить для изотермического, адиабатного и политропного сжатия. Все три процесса сжатия представить на диаграммах в  - и
- и  - координатах.
- координатах.
Газ – водород ( ): газовая постоянная R = 4124
): газовая постоянная R = 4124  , молекулярная масса μ = 2,016 кг/кмоль. Показатель адиабаты k = 1,41, показатель политропны n = 1,4 – задано.
, молекулярная масса μ = 2,016 кг/кмоль. Показатель адиабаты k = 1,41, показатель политропны n = 1,4 – задано.
Параметры газа в точке 1 – начало всех процессов: давление  =
=  = 0,1 МПа; температура
= 0,1 МПа; температура  = 300,15 K; объем
= 300,15 K; объем 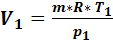 =
=  = 346,59
= 346,59  .
.
Изотермический процесс.
Параметры газа в точке 2–конец процесса 1–2: температура  =
=  = 300,15 K
= 300,15 K
объем  = 0,1 *
= 0,1 *  = 0,1 * 346,59 = 34,659
= 0,1 * 346,59 = 34,659  ; давление
; давление  ≈ 1 *
≈ 1 *  = 1 МПа; работа
= 1 МПа; работа  =
=  *
* 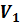 * ln
* ln  = 0,1 *
= 0,1 *  * 346,59 * ln
* 346,59 * ln  = - 0,312 *
= - 0,312 * 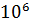 Дж = - 312 кДж – знак «-», значит работа затрачивается, так как процесс сжатия;
Дж = - 312 кДж – знак «-», значит работа затрачивается, так как процесс сжатия;  =
=  = - 312 кДж – знак «-», значит теплота отводится; изменение внутренней энергии и энтальпии
= - 312 кДж – знак «-», значит теплота отводится; изменение внутренней энергии и энтальпии  = 0,
= 0,  = 0 – так как
= 0 – так как  =
=  ; изменение энтропии
; изменение энтропии  = m * R * ln
= m * R * ln  = 28 * 4124 * ln
= 28 * 4124 * ln  = - 265585,6
= - 265585,6  = - 265,586
= - 265,586  - знак «-», значит энтропия уменьшается, так как теплота отводится.
- знак «-», значит энтропия уменьшается, так как теплота отводится.
Адиабатный процесс.
Параметры газа в точке 2'–конец процесса 1–2: объем  = 0,1 *
= 0,1 *  = 0,1 * 346,59 = 34,659
= 0,1 * 346,59 = 34,659  ;
;  =
=  →
→  =
=  =0,1*
=0,1*  =2,57 МПа;
=2,57 МПа;  =
=  →
→  =
=  = 300,15 *
= 300,15 *  = 771,5 К;
= 771,5 К;
работа  = m *
= m * 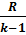 * (
* (  ) = 28*
) = 28*  - 132,75 *
- 132,75 *  Дж = - 132,75 МДж – работа, затрачивается; количество теплоты и изменение энтропии
Дж = - 132,75 МДж – работа, затрачивается; количество теплоты и изменение энтропии  = 0;
= 0;  = 0 – так как в адиабатном процессе теплота не подводится и не отводится; изменение внутренней энергии
= 0 – так как в адиабатном процессе теплота не подводится и не отводится; изменение внутренней энергии  = -
= -  = - (-132,75) = 132,75 МДж; изменение энтальпии
= - (-132,75) = 132,75 МДж; изменение энтальпии  = m *
= m *  * (
* (  -
-  ) – изобарную теплоемкость
) – изобарную теплоемкость  принимаем независимой от температуры, тогда для двухатомных газов
принимаем независимой от температуры, тогда для двухатомных газов  =
=  = 14,534
= 14,534 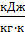 ,
,  = 28 * 14,534 * (771,5 – 300,15) = 191816,8252 кДж = 191,8 МДж.
= 28 * 14,534 * (771,5 – 300,15) = 191816,8252 кДж = 191,8 МДж.
Политропный процесс.
Параметры газа в точке 2''–конец процесса 1–2: объем  = 0,1 *
= 0,1 *  = 0,1 * 346,59 = 34,659
= 0,1 * 346,59 = 34,659  ; из зависимости между параметрами в политропном процессе
; из зависимости между параметрами в политропном процессе  =
=  = 0,1*
= 0,1*  = 2,51 МПа;
= 2,51 МПа;  =
=  = 300,15 *
= 300,15 *  = 753,94 К; работа
= 753,94 К; работа  = m *
= m *  * (
* (  ) = 28*
) = 28* 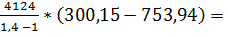 - 131 *
- 131 *  Дж = - 131 МДж – работа, затрачивается; количество
Дж = - 131 МДж – работа, затрачивается; количество  = m
= m 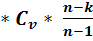 *
* 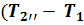 ) – массовая изохорная теплоемкость
) – массовая изохорная теплоемкость  =
=  =
=  = 10,376
= 10,376 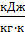 тогда
тогда  = 28 * 10,376 *
= 28 * 10,376 *  * (753,94 – 300,15) = - 3,296 МДж – знак «-», значит теплота отводится; изменение внутренней энергии
* (753,94 – 300,15) = - 3,296 МДж – знак «-», значит теплота отводится; изменение внутренней энергии  =
=  =
=  * (-132,75) = 129,51 МДж или
* (-132,75) = 129,51 МДж или  = -3,296 – (- 131) = 127,704 МДж, погрешность
= -3,296 – (- 131) = 127,704 МДж, погрешность  =
=  * 100% = 1,41%
* 100% = 1,41%  3%; так как k
3%; так как k  n
n  1, то для процесса сжатия теплота отводится, внутренняя энергия газа увеличивается, изменение энтальпии
1, то для процесса сжатия теплота отводится, внутренняя энергия газа увеличивается, изменение энтальпии  = m *
= m *  * (
* (  -
-  ) = 28 * 14,534 * (753,94 – 300,15) = 184670,7481 кДж = 184,67 МДж; изменение энтропии
) = 28 * 14,534 * (753,94 – 300,15) = 184670,7481 кДж = 184,67 МДж; изменение энтропии  = m *
= m *  *
*  * ln
* ln  = 28 * 14,534 *
= 28 * 14,534 *  * ln
* ln  = - 9,37
= - 9,37  - знак «-», значит энтропия уменьшается, так как теплота
- знак «-», значит энтропия уменьшается, так как теплота  отводится.
отводится.
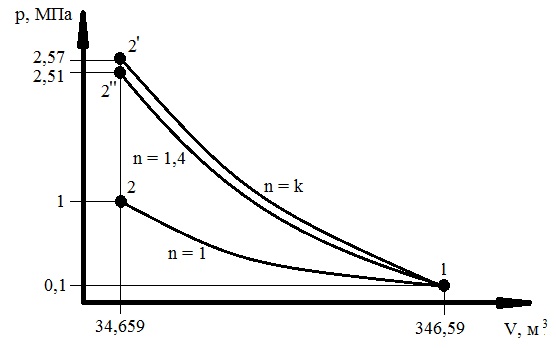
Процессы на диаграммах в  - и
- и  - координатах
- координатах

Задача 6.
В двух теплоизолированных баллонах содержится по 1 кг газа при одинаковых температурах  =
=  = 20
= 20 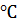 (
( =
=  = 293,15 K), но при разных давлениях
= 293,15 K), но при разных давлениях  = 0,18 МПа и
= 0,18 МПа и  = 0,52 МПа. После сообщения баллонов между собой давление в них выравнивается. Определить происходящее при этом изменение энтропии газа.
= 0,52 МПа. После сообщения баллонов между собой давление в них выравнивается. Определить происходящее при этом изменение энтропии газа.
Газ – окись углерода (СО), газовая постоянная R = 296,8  , теплоемкость не зависит от температуры, μ = 28,01кг/кмоль, массовая изобарная теплоемкость
, теплоемкость не зависит от температуры, μ = 28,01кг/кмоль, массовая изобарная теплоемкость  =
= 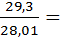 1,046
1,046  .
.
Параметры газа в баллонах до их сообщения:
Первый баллон:  = 1 кг,
= 1 кг,  = 0,18 МПа,
= 0,18 МПа,  = 293,15 K, объем
= 293,15 K, объем 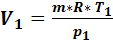 =
= 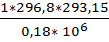 =0,484
=0,484  .
.
Второй баллон:  = 1 кг,
= 1 кг,  = 0,52 МПа,
= 0,52 МПа,  = 293,15 K, объем
= 293,15 K, объем 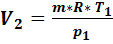 =
=  =0,167
=0,167  .
.
Параметры газа в баллонах после их сообщения:
 =
=  +
+  = 0,484 + 0,167 = 0,651
= 0,484 + 0,167 = 0,651  ,
,  =
=  +
+  = 1 + 1 = 2 кг,
= 1 + 1 = 2 кг,  =
=  =
=  = 293,15 К, давление
= 293,15 К, давление  =
=  =
=  = 267302,36 Па = 0,267 МПа.
= 267302,36 Па = 0,267 МПа.
Нормальные условия: 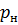 = 0,1 МПа,
= 0,1 МПа,  = 273,15 К.
= 273,15 К.
Изменение энтропии:
Первый баллон:  =
=  -
-  =
=  * ln
* ln  – R * ln
– R * ln  = 1.046 * ln
= 1.046 * ln  – 296.8 *
– 296.8 *  * ln
* ln  = - 0,1
= - 0,1 
Второй баллон:  =
=  -
-  =
=  * ln
* ln  – R * ln
– R * ln  = 1.046 * ln
= 1.046 * ln  – 296.8 *
– 296.8 *  * ln
* ln 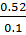 = - 0,414
= - 0,414 
После сообщения баллонов:  =
=  -
-  =
=  * ln
* ln  – R * ln
– R * ln  = 1.046 * ln
= 1.046 * ln  – 296.8 *
– 296.8 *  * ln
* ln  = - 0,217
= - 0,217 
Изменение энтропии газа после сообщения баллонов: 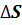 =
=  *
*  - (
- (  *
*  +
+  *
*  ) = 2 – (- 0,217) * (1 * (- 0,1) + 1 * (- 0,414)) = 1,888
) = 2 – (- 0,217) * (1 * (- 0,1) + 1 * (- 0,414)) = 1,888 
Задача 7.
Цикл описывается тремя термодинамическими процессами, характеризующимися показателями  = 0,6;
= 0,6; 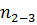 =
=  ;
;  = k. За процесс 1 - 2 изменение объема рабочего тела составляет
= k. За процесс 1 - 2 изменение объема рабочего тела составляет  /
/  = 9. Начальные параметры состояния рабочего тела: избыточное давление
= 9. Начальные параметры состояния рабочего тела: избыточное давление  = 0,08 МПа и температура
= 0,08 МПа и температура  = 427
= 427 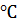 (
( = 700,15 K). Количество газа 1 кг. Рабочее тело – воздух: газовая постоянная R = 287,08
= 700,15 K). Количество газа 1 кг. Рабочее тело – воздух: газовая постоянная R = 287,08  , μ = 28,96 кг/кмоль, показатель адиабаты k = 1,4.
, μ = 28,96 кг/кмоль, показатель адиабаты k = 1,4.
Определить:
1. Основные параметры  характерных состояний рабочего тела;
характерных состояний рабочего тела;
2. Изменение энтропии в процессе 1-2.
3. Степень термодинамического совершенства цикла (рассчитать термодинамический к.п.д. или холодильный коэффициент в зависимости от того, прямой цикл или обратный).
Представить данный цикл в диаграммах  и
и  , указав на них площади, соответствующие подведенной
, указав на них площади, соответствующие подведенной  и отведенной
и отведенной  удельной теплоте.
удельной теплоте.
 = 0,6 – процесс политропный,
= 0,6 – процесс политропный, 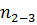 =
=  - процесс изохорный;
- процесс изохорный;  = k – процесс адиабатный.
= k – процесс адиабатный.
Параметры состояния рабочего тела в характерных точках цикла:
Точка 1. – начало политропного процесса 1 – 2: абсолютное давление  =
= 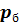 +
+  = 0,1 + 0,08 = 0,18 МПа; удельный объем
= 0,1 + 0,08 = 0,18 МПа; удельный объем  =
=  (так как m = 1 кг) =
(так как m = 1 кг) =  = 2,278
= 2,278  .
.
Точка 2. – конец политропного процесса 1–2 и начало изохорного процесса 2-3: удельный объем  =
=  / 9 = 2,278 / 9 = 0,253
/ 9 = 2,278 / 9 = 0,253  ; в политропном процессе
; в политропном процессе  =
=  →
→  =
=  *
*  = 0,18 *
= 0,18 *  = 0,67 МПа, температура
= 0,67 МПа, температура  из уравнения
из уравнения 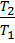 =
=  →
→  =
=  *
*  = 700,15 *
= 700,15 *  =290,73 К.
=290,73 К.
Точка 3. –конец изохорного процесса 2–3, начало адиабатного процесса 3-1:
Удельный объем 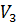 =
=  = 0,253
= 0,253  ; для определения давления
; для определения давления 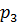 используем зависимость между параметрами в адиабатном процессе 3-1
используем зависимость между параметрами в адиабатном процессе 3-1 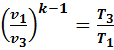 →
→  =
=  *
*  = 700,15 *
= 700,15 *  = 1686,41 К;
= 1686,41 К;
давление  =
=  =
=