Список экзаменационных задач к экзамену по информатике 10 класс
1. Постройте и упростите логические выражения, соответствующие приведённым таблицам истинности. В каждом случае выбирайте наиболее простой способ синтеза. В вашем решении опишите все шаги алгоритма.
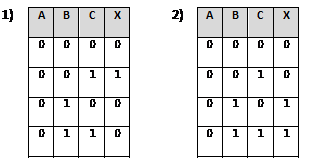
Решите логические задачи наиболее подходящим способом
Задача 1.
Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:
Алеша. Это сосуд греческий и изготовлен в V веке. Боря. Это сосуд финикийский и изготовлен в III веке. Гриша. Это сосуд не греческий и изготовлен в IV веке.
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений.
Где и в каком веке изготовлен сосуд?
Задача 2.
После традиционного вечера встречи с выпускниками школы в стенгазете появилась заметка о трех наших бывших учениках. В ней было сказано, что Иван, Андрей и Борис стали учителями. Теперь они преподают разные дисциплины: один из них — математику, второй — физику, а третий — химию. Живут они тоже в разных городах: Минске, Витебске, Харькове. В заметке было также написано, что их первоначальные планы осуществились не полностью:
Иван живет не в Минске;
Андрей — не в Витебске;
житель Минска преподает не математику;
Андрей преподает не физику;
повезло только жителю Витебска: он преподает любимую им химию.
Можно ли по этим данным определить, кто, где живет и что преподает?
Задача 3
В конструкторском бюро работают Антонов, Борисов, Кириллов и Дроздов. Все хотят отдыхать летом, и поэтому при составлении графика отпусков всегда возникают бесконечные споры. Попробуйте помочь составить график отпусков на 4 года, который бы удовлетворял следующим пожеланиям сотрудников:
1. в отпуск сотрудники хотят идти только с мая по август;
2. продолжительность отпуска — один месяц;
3. в каждом месяце в отпуск может пойти только один человек;
4. за четыре года каждый из четырех сотрудников должен получить
отпуск по одному разу в каждом из этих месяцев;
5. в первый год Кириллов хочет отдыхать в июле;
6. во второй год Антонову отпуск нужен в мае;
7. в третий год Дроздову отпуск нужен в июне;
8. Борисов на четвертый год предполагает уйти в отпуск в июле;
в августе все хотят отдыхать следующим образом: в первый год —
Дроздов, во второй — Кириллов, в третий — Борисов, в четвертый —
Антонов.
Требуется определить, кто есть кто.
Задача 4.
В одном доме живут Воронов, Павлов, Журавлев, Синицын. Один из них — математик, другой — художник, третий — писатель, а четвертый— баянист. Известно, что:
1. ни Воронов, ни Журавлев не умеют играть на баяне;
2. Журавлев не знаком с Вороновым;
3. Писатель и художник в воскресенье уезжают на дачу к Павлову
4. Писатель собирается написать очерк о Синицыне и Воронове
Требуется определить, кто есть кто
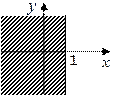
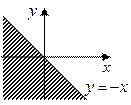
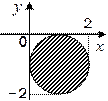
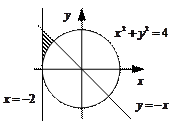
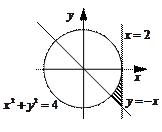
3. Задайте с помощью предиката 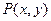 множество точек, соответствующее заштрихованной области на плоскости.
множество точек, соответствующее заштрихованной области на плоскости.
| 1. | 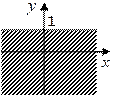
| 
| 
|
| 2. | 
| 
| 
|
| 3. | 
| 
| 
|
| 4. | 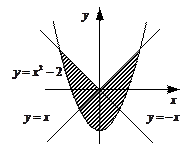
| 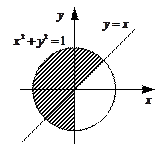
| 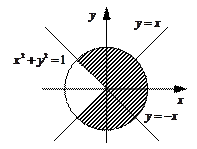
|
Постройте схему, соответствующую заданной логической функции, на логических элементах «И», «ИЛИ» и «НЕ». Предварительно преобразуйте выражение так, чтобы количество использованных логических элементов было минимальным.
1. 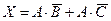
2. 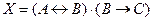
3. 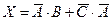
4. 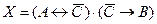
5. 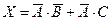
6. 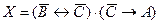
5.Упростить следующие выражения:
1. (X v Z v Y) & (X v Y v Z) & (X v Y v Z)
2. (A v B) v A v F & E v B
3. X v T & Y & Z & (X v T)
4. (A v B v C) & (A v B v C) & (A v B v C)
5. (X v Y v Z) & (X v Y v Z) & (X v Y v Z)
1) Логическая функция F задаётся выражением (x Ú y Ú z) Ù (x Ú y Ú w). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
2) Логическая функция F задаётся выражением (x Ù (y Ú z) Ù (z Ú w) Ù (y Ú w)). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
3) Логическая функция F задаётся выражением x Ú (z Ù w) Ú (y Ù w) Ú (y Ù z). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
4) Логическая функция F задаётся выражением x Ú (y Ù z) Ú (y Ù w) Ú (z Ù w). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
5) Логическая функция F задаётся выражением (z Ú y) ® (x º z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| ? | ? | ? | F |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
6) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Суфле | Корзина | Эклер
7) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| Стольник | 375 |
| Рында | 315 |
| Парус | 290 |
| Стольник & Рында | 85 |
| Стольник & Парус | 0 |
| Стольник | Рында | Парус | 840 |
Сколько страниц (в тысячах) будет найдено по запросу
Парус & Рында
8) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| Слобода | 515 |
| Пилигрим | 175 |
| Пилигрим & Равелин | 105 |
| Слобода & Равелин | 70 |
| Слобода & Пилигрим | 0 |
| Слобода | Равелин | Пилигрим | 765 |
Сколько страниц (в тысячах) будет найдено по запросу
Равелин
9) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| (Суворов & Альпы) | (Суворов & Варшава) | 1100 |
| Суворов & Варшава | 600 |
| Суворов & Варшава & Альпы | 50 |
Сколько страниц (в тысячах) будет найдено по запросу
Суворов & Альпы
10) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| (Испания & Америка) | (Испания & Индия) | 2800 |
| Испания & Америка | 1600 |
| Испания & Индия & Америка | 150 |
Сколько страниц (в тысячах) будет найдено по запросу
Испания & Индия
11) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| (макаки | павианы & гиббоны) & шимпанзе | 154 |
| шимпанзе & павианы & гиббоны | 120 |
| шимпанзе & макаки & павианы & гиббоны | 32 |
Сколько страниц (в тысячах) будет найдено по запросу
макаки & шимпанзе
12) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| Пушкин & Лермонтов | 540 |
| Лермонтов & Толстой & Достоевский | 280 |
| Толстой & Лермонтов & Пушкин & Достоевский | 150 |
Сколько страниц (в тысячах) будет найдено по запросу
(Пушкин | Толстой & Достоевский) & Лермонтов
13) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| (галера | бриг & фрегат) & корвет | 620 |
| галера & корвет | 560 |
| фрегат & галера & корвет & бриг | 70 |
Сколько страниц (в тысячах) будет найдено по запросу
корвет & бриг & фрегат
14) В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| (стол | стул & диван) & кровать | 890 |
| стол & кровать | 780 |
| кровать & стул & диван | 320 |
Сколько страниц (в тысячах) будет найдено по запросу
диван & стол & кровать & стул
Задачи на тему «Хранение чисел в памяти компьютера»
1. Записать следующие числа в форме с плавающей запятой и нормализованной мантиссой:
а) 217, 93410; б) 7532110; в) 10,010110; г) 20045010
2. Компьютер работает только с целыми положительными числами. Каков диапазон изменения чисел, если для представления числа в памяти компьютера отводится 4 байта?
3. Пусть для представления целых чисел в компьютере используется 16-разрядная ячейка (2 байта). Определить каков диапазон хранимых чисел, если:
а) используются только положительные числа;
б) используются как положительные, так и отрицательные числа в равном количестве.
4. Записать внутреннее представление числа в форме с плавающей точкой:
a) 250,85 b) 223,25 c) -22,34
5. По шестнадцатеричной форме внутреннего представления числа в форме с плавающей точкой С9811000 восстановить само число
6. Представить числа в прямом, обратном и дополнительном кодах, интерпретируя их как восьмибитовое целое со знаком: 13 и -19.
7. Запишите в десятичной системе счисления целое число, если дан его дополнительный код:
a) 0110101101111000; b) 1110100100110101;