В схеме (рис. 5.1,а) общий ток, согласно первому закону Кирхгофа, равен геометрической сумме токов в параллельных ветвях:
(5.1)
|
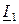совпадает по фазе с напряжением 
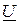, а ток 
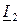опережает напряжение 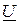на угол 900.
Рис.5.1. Разветвленная цепь RC (а) и ее векторная диаграмма (б) при C=const и R=var.
Если 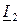= const, a 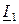изменяется от 0 до ¥, сохраняя неизменным направление (j 1 = 0=const), то геометрическим местом концов вектора 
является прямая линия AN’, проведенная из конца вектора 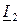под углом к вектору 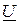(угол j 1 = 0).
Таким образом, уравнение (5.1) есть уравнение прямой линии в комплексной форме записи.
Диаграмма, представленная на рис. 5.1,б называется линейной диаграммой. Чтобы найти ток для заданного значения 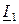(или y 1 = g 1) надо на прямой AN’ отложить значение тока 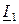в масштабе m I (или значение g 1, в масштабе m g = m I / U). Полученную точку N соединить с точкой О.
При изменении емкости конденсатора в схеме (рис. 5.2,а) геометрическим местом концов вектора 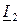является окружность, а уравнение:
(5.2)
при R 2 = const и XC = var является уравнением окружности в символической форме записи.
Если в разветвленной цепи сопротивление одной из ветвей (например R 1 в схеме рис. 5.2,а), а следовательно и ток в ней остаются неизменными, а ток в другой ветви изменяется по круговой диаграмме, то геометрическим местом концов вектора тока также является дуга окружности.
Для построения круговой диаграммы задаемся масштабами по напряжению, току и сопротивлению – mu; mI; mz и откладываем в принятых масштабах векторы 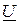и 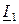(рис. 5.2,б). Конец вектора 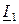принимаем за начало О1 для построения круговой диаграммы 
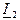. Находим значение тока 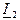при коротком замыкании на зажимах конденсатора, т.е. при XС = 0
(5.3)
Ток 
совпадает по фазе с напряжением 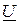. Из точки О1 откладываем отрезок О1К = I 2k /m I, по направлению вектора 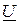. Отрезок О1К является хордой круговой диаграммы 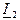. В масштабе mz откладываем по направлению отрезка О1К отрезок О1А = R2 /mz и из точки А под углом 900 к линии О1К проводим линию изменяющегося параметра AN’. Перпендикуляр, к линии изменяющегося параметра, опущенный из точки О1 совпадает по направлению с хордой. Поэтому хорда О1К является и диаметром круговой диаграммы. Разделив отрезок О1К пополам, находим центр окружности С и проводим дугу окружности в сторону,линии изменяющегося параметра.
|
Рис.5.2. Разветвленная цепь RC (а) и ее круговая диаграмма (б) при R1= const, R2=const и С=var.
Чтобы определить электрические величины при заданном значении ХС, надо отложить на прямой AN’ отрезок АN = XC /mz; точку N соединить с точкой О1 и точку М с точкой О. Тогда электрические величины определяются:
I 1 = m 1*OО1 I2 = m 1*О1М
I = m 1*OМ S = m S*OМ
P = m P*OF Q = m Q *МF
m р = m Q = m S = m l* U cosj = OF/OM
Порядок выполнения работы
1. Выбрать в меню лабораторную работу “5.1. Исследование параллельной цепи RC при R1=var ” (рис.5.3). Параметры схемы устанавливает компьютер по шифру студента
2.. Исследовать схему при изменении сопротивления R 1 от максимума до минимума ( ток I1 во время опыта не должен превышать 1А ). Результаты измерений записать в таблицу 5.1 (8-9 значений).
Таблица 5.1
| № п/п | Измерено | Вычислено | |||||||||
| U | I | I1 | I2 | R1 | Z | Z2 | P | cos j | Q | S | |
| В | А | А | А | Ом | Ом | Ом | Вт | - | вар | ВА | |
| 0.855 | 0.143 | 0.843 | 601.39 | 100.58 | 102.01 | 12.298 | 0.16 | 72.498 | 73.53 |
Формулы для расчетов: R 1 = U / I 1; Z = U / I; Z 2 = X С = U / I 2; P = UI 1; cos j = P / UI; Q = UI 2; S = UI; 
.
По данным таблицы 5.1 построить в одних осях координат зависимости I; I 1; I 2; P; cos j = f (R 1).
3. Построить линейную диаграмму токов. По указанию преподавателя для одного из замеров таблицы 5.1 найти по диаграмме значение тока I и сравнить его с измеренным.
4. Выбрать в меню лабораторную работу “5.2. Исследование параллельной цепи RC при C=var ” (рис.5.4). Параметры схемы устанавливает компьютер по шифру студента. Исследовать схему при изменении емкости С от максимального значения до нуля для 8-9 значений емкости С. Результаты измерений записать в
таблицу 5.2.
Таблица 5.2
| № п/п | Измерено | Вычислено | |||||||||||
| U | С | I | I1 | I2 | R1 | Z2 | XС | R2 | Р | сosj | Q | S | |
| В | мкФ | А | А | А | Ом | Ом | Ом | Вт | Вт | - | вар | ВА | |
| 0.855 | 0.143 | 0.754 | 0.843 | 601.39 | 100.58 | 602.3 | 12.298 | 0.16 | 72.49 | 73.53 |
Формулы для расчетов: R 1 = U / I 1 ; X С = 1/ w ×C; w = 314 1/C ;
Z 2 = U / I 2 ; 
;
5. Результаты расчетов (табл.5.1 и табл.5.2) занести для проверки в таблицу 5.3 в компьютере (вызвав ее из меню);
Таблица 5.3
| По данным табл.5.1 | По данным табл. 5.2 | ||
| XC | C | R1 | R2 |
| Ом | мкФ | Ом | Ом |
| 0.855 | 601.39 | 602.3 |
Ответы:
Линейная диаграмма
Линейные диаграммы используются для характеристики вариации, динамики и взаимосвязи. Линейные графики строятся на координатной сетке. Геометрическими знаками служат точки и отрезки прямой, которые их последовательно соединяют в ломаные.
Линейные диаграммы для характеристики динамики применяют в следующих случаях:
§ если количество уровней ряда динамики достаточно велико. Их применение подчеркивает непрерывность процесса развития в виде непрерывной линии;
§ с целью отображения общей тенденции и характера развития явления;
§ при необходимости сравнения нескольких динамических рядов;
§ если нужно сопоставить не абсолютные уровни явления, а темпы роста.
2. Круговая диаграмма
Круговые диаграммы строятся в виде площади кругов, радиусы которых равны корню квадратному из значений показателя.
Секторная диаграмма
3. Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями.