Подставив в формулу (9) вместо 
сумму 
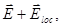и учитывая(17), получим:
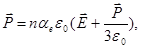(18)
Вектора 
и параллельны, поэтому для их модулей справедливо равенство:
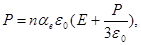(19)
откуда следует
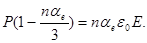(20)
Из (7) следует, что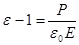 
. Учитывая это, из (20) имеем:
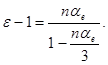(21)
Прибавив к обеим частям последнего уравнения тройку, получим:
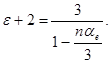(22)
Разделив (21) на (22) почленно, получим:
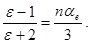(23)
Формула (23) называется формулой Клаузиуса-Моссотти. Она справедлива только для неполярных диэлектриков. Ланжевен и Дебай обобщили её на случай полярных диэлектриков, в которых проявляется как электронная, так и ориентационная поляризация. Соответствующее выражение, носящее название формула Ланжевена-Дебая с учетом (13) имеет вид:
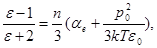(24)
Последняя формула позволяет определить величину дипольного момента полярной молекулы ро. Если в диэлектрике имеют место все три типа поляризации, то формула (24) приобретает вид:
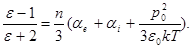(25)
На рис.7 приведены зависимости, описываемые соотношением (25), при различных механизмах поляриэации.
Исследуя на опыте зависимость ε от Т, можно получить зависимость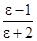 
от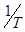 
и по данной зависимости определить, какой тип поляризации имеет место в данном диэлектрике.
Обычный метод измерения ε основан на сопоставлении емкости С2 плоского конденсатора, у которого пространство между пластинами заполнено диэлектриком, с емкостью С1 конденсатора, имеющего аналогичные пластины, но без диэлектрика между ними. Емкости С1 и С2 выражаются формулами:
, 
,
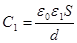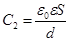где ε1 - диэлектрическая проницаемость воздуха, ε - диэлектрическая проницаемость вещества, заполняющего конденсатор, S – площадь пластин, d – расстояние между пластинами.
|
|
Так как диэлектрическая проницаемость воздуха близка к единице, то отношение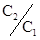 
как раз и равно диэлектрической проницаемости вещества, заполняющего пространство между пластинами.
 |
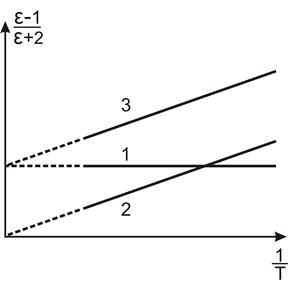Рис. 7.
1-электронная поляризуемость; 2- ориентационная поляризуемость;
3-оба типа поляризуемости
Такой способ использован в данной лабораторной работе для определения зависимости диэлектрической проницаемости жидкого диэлектрика от температуры.
Описание лабораторной установки
Упрощенная схема лабораторной установки представлена на рис. 8.
Исследуемый жидкий диэлектрик находится в стеклянном сосуде цилиндрической формы. Сосуд закреплен в специальном блоке. В этом блоке находится также автотрансформатор. Для измерения диэлектрической проницаемости используется металлический конденсатор переменной емкости, состоящий из двух одинаковых секций. Одна из секций погружена в масло, а другая находится в воздухе. Следовательно, отношение емкости С2 секции, погруженной в масло, к емкости СI секции, находящейся в воздухе, равно величине диэлектрической проницаемости:
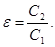(26)
Нагрев исследуемого диэлектрика осуществляется путем пропускания тока через проводник в виде спирали. Температура контролируется с помощью специального датчика, помещенного в диэлектрик и подключенного к цифровому вольтметру В7-27. Показания вольтметра соответствуют температуре, выраженной в градусах Цельсия. Регулировка тока через спираль производится автотрансформатором.
 |
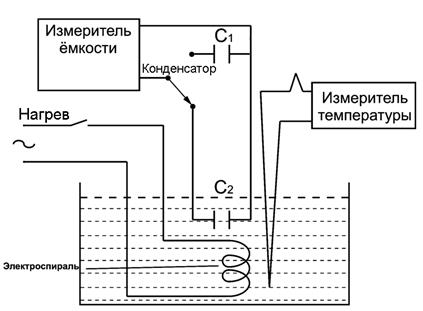Рис. 8. Схема лабораторной установки
|
|
Назначение тумблеров и гнезд на передней панели блока, в котором находится изучаемый диэлектрик, следующее. Тумблер «Сеть» подключает автотрансформатор к сети. Тумблером «Нагрев» спираль, предназначенная для нагрева диэлектрика, подключается к выходу автотрансформатора. Тумблер «Конденсатор» подсоединяет к гнездам «С1, С2» верхнюю секцию конденсатора, если он находится в положении «С1», и нижнюю, если он находится в положении «С2». На верхней крышке блока расположены рукоятка регулировки перекрытия пластин конденсатора (впереди) и рукоятка автотрансформатора, с помощью которой регулируется напряжение на нагревательной спирали.
Задание
1. Изучить основные понятия физики диэлектриков.
2. Строго руководствуясь инструкцией по выполнению лабораторной работы, измерить емкости С1 и С2 при комнатной температуре. Затем включить нагрев спирали и снять зависимость емкости С2 от температуры с шагом 5оС. Нагрев спирали отключить по достижении температуры 90оС. Результаты измерений и вычислений занести в табл.1 (графы 1,2,4).
3. Расcчитать величину e при различных температурах по формуле (26) с точностью до 4 значащих цифр. Результаты внести в столбец 3.
4. Рассчитать температуру в градусах Кельвина (Т) и обратную температуру (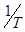) с точностью до трех значащих цифр и внести данные в столбцы 5 и 6.
5. Рассчитать величину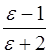 
с точностью до трех значащих цифр для всех температур. Результаты внести в столбец 7.
6. Используя данные столбцов 6 и 7, построить график зависимости 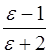от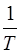 
.
7. На основании полученного графика сделать вывод о механизмах поляризации в исследованном диэлектрике.
|
|
8. Определить для данного вещества при комнатной температуре, какую долю от полной поляризуемости составляет электронная поляризуемость.
Результаты измерений и вычислений
Т а б л и ц а 1
| С1, пФ | С2, пФ | ε | Температура диэлектрика t,оС | Т, К |
|
|
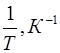
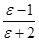
Вопросы
1. Что такое диэлектрики?
2. Что такое электрический диполь? Какие величины характеризуют диполь?
3. Какие молекулы относятся к неполярным и полярным?
4. В чем заключается явление поляризации? Что такое вектор поляризации?
5. Как происходит электронная, ориентационная и ионная поляризация? Как зависят от температуры соответствующие поляризуемости?
6. Что такое макроскопическое и микроскопическое поле?
7. Что такое вектор электрической индукции?
8. Приведите формулу Лоренца. Что она учитывает?
9. Приведите формулы Клаузиуса – Моссотти и Ланжевена –Дебая.
Литература
1. Савельев И.В. Курс общей физики. –М.: Наука, 1988, т.2, с. 60 – 77.
2. Савельев И.В. Курс физики. – М.: Наука, 1989, т.2, с.55 – 73.
3. Трофимова Т.И. Курс физики. М.: Издательский центр «Академия», 2007, с. 160 – 166.
4. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 2001, с. 202 – 210.
5. Наркевич И.И., Волмянский Э.И., Лобко С.И. Физика. – Мн.: Новое знание, 2004, с.286 – 298