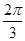|
или 1200 (рис. 9.1).
Рис.9.1. Синусоидальные ЭДС одной частоты, образующие симметричную трехфазную систему.
Трехфазная система переменного тока, изобретенная русским инженером М.О. Доливо-Добровольским в 1891 году, получила широкое распространение во всем мире. Отдельные электрические цепи, входящие в состав трехфазной системы, называются фазами.
|
а
|
б
|
в
Рис.9.2. Фазы и векторная диаграмма трехфазного источника питания (а); четырехпроводная (б) и трехпроводная (в) схемы соединения звездой.
Источником энергии в трехфазной системе являются генератор или трансформатор, имеющие три обмотки. Будем называть эти устройства в общем случае трехфазным источником питания. Начала обмоток (или начала фаз) трехфазного источника питания обозначаются прописными начальными буквами латинского алфавита A, B и C, а концы – прописными конечными буквами X, Y и Z (рис.9.2, а). Порядок букв обозначает порядок чередования фаз, т. е. последовательность прохождения ЭДС через амплитудные или нулевые значения. Положительные направления ЭДС в обмотках источника питания выбираются от концов к началам. Фазы источника питания на электрической схеме (рис.2.9.2, а) изображены под углом 1200 для того, чтобы подчеркнуть, что ЭДС в них сдвинуты на одну треть периода.
Для соединения трехфазного источника энергии звездой концы его обмоток соединяют в одну общую точку N. Эта точка называется нейтральной точкой (или нейтралью) источника питания (рис. 9.2, б). Аналогично, для соединения трехфазного приемника электрической энергии звездой необходимо концы сопротивлений всех трех фаз также соединить в одну общую точку n . Эта точка называется нейтральной точкой (или нейтралью) приемника. Начала фаз генератора A, B, C и соответствующие начала фаз приемника a, b, c соединяются линейными проводами. Нейтральные точки источника питания (N) и приемника (n) могут соединяться друг с другом нейтральным проводом (4-х проводная система, (рис. 9.2 ,б)) или не соединяться (трехпроводная система (рис.9.2, в)).
|
|
Фазные напряжения источника питания отличаются от его фазных ЭДС на величину падения напряжения в обмотках. Мы будем пренебрегать сопротивлениями обмоток ввиду их малости и считать трехфазный источник ЭДС идеальным. В этом случае фазные напряжения источника питания равны соответствующим фазным ЭДС: 
. В симметричной системе фазные напряжения источника питания изображаются на комплексной плоскости тремя равными по величине векторами, сдвинутыми по фазе на угол 1200 (рис.9.2, а).
|
Рис.9.3. Векторы фазных и линейных напряжений в симметричной трехфазной системе, соединенной звездой.
Вектор напряжения в фазе А обычно откладывают по действительной положительной оси, направленной вертикально вверх, а не вправо, как это было принято в однофазных цепях. Систему фазных напряжений источника питания для действующих значений можно записать в комплексной форме следующим образом:
; 
; 
. (9.1)
Из векторной диаграммы (рис. 9.2, а) нетрудно видеть, что векторы фазных напряжений источника питания образуют симметричную звезду, лучи которой исходят из нейтральной точки N источника питания. Очевидно, что сумма векторов фазных напряжений симметричной трехфазной системы равна нулю.
|
|
Напряжения между линейными проводами называют линейными напряжениями. Линейные напряжения связаны с фазными напряжениями следующими соотношениями (рис.9.2 ,б):
; 
; 
. (9.2)
Таким образом, линейные напряжения равны геометрической разности соответствующих фазных напряжений. Графическое изображение вектора линейного напряжения 
в соответствии с первым уравнением (9.2.) показано на рис.9.3. Из диаграммы видно, что линейное напряжение равно вектору, проведенному в точку А из точки В. Вектор линейного напряжения опережает по фазе вектор фазного напряжения 
на 300. На топографической диаграмме (рис.9.4) показаны векторы всех трех линейных напряжений генератора. На этой диаграмме потенциал нейтральной точки N источника питания принят за ноль и потенциалы всех других точек схемы откладываются именно от этой точки. Каждой точке на схеме соответствует точка на топографической (потенциальной) диаграмме.
|
Рис.9.4. Топографическая диаграмма линейных и фазных напряжений трехфазного источника питания.
Из приведенных топографических диаграмм видно, что при симметричной системе фазных напряжений система линейных напряжений также симметричная. Векторы линейных напряжений образуют равносторонний треугольник.
Действующие значения линейных напряжений можно выразить через фазные напряжения следующим образом (рис.9.3):
|
|
. (9.3)
Если обозначить линейные напряжения 
, а фазные 
, то соотношение между ними запишется как 
, т. е. линейное напряжение при соединении звездой в 
раз больше фазного напряжения. Наличие двух напряжений в четырехпроводной системе позволяет подключать к ней приемники энергии с номинальным напряжением, равным фазному напряжению (например, 220В) и с номинальным напряжением, равным линейному напряжению (например, 380В).
В четырехпроводной системе фазные напряжения 
приемников меньше соответствующих фазных напряжений источника питания 
из-за падения напряжения в соединительных проводах. Мы будем пренебрегать сопротивлением проводов (нейтрального и линейных) и считать, что фазные напряжения приемника равны фазным напряжениям источника питания:
(9.4)
С учетом (9.4) топографическая диаграмма фазных и линейных напряжений в симметричной нагрузке при четырехпроводной системе будет такая же, как и диаграмма на рис 9.4, если заменить прописные буквы A, B, C на строчные a, b, c.
Токи в фазах генератора и приемника называются фазными токами IФ, а токи, протекающие в линейных проводах – линейными токами IЛ. При соединении приемников электрической энергии звездой линейные провода соединены последовательно с фазами генератора и приемника, поэтому очевидно, что фазные токи равны линейным токам, т.е.: 
.
В четырехпроводной системе, пренебрегая сопротивлением соединительных проводов, получаются три независимых контура и комплексы фазных токов можно определить по закону Ома:
; 
; 
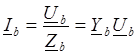. (9.5)
Здесь - 
- комплексные сопротивления фаз нагрузки,
- комплексные проводимости фаз нагрузки.
На рис.9.5. показана векторная диаграмма напряжений и токов для равномерной активной нагрузки при симметричной системе питающих напряжений.
Векторы тока равны по значению и совпадают по фазе с напряжениями. Таким образом, они тоже сдвинуты друг относительно друга на одну треть периода и образуют так называемый трехфазный ток. В четырехпроводной системе ток в нейтральном проводе по первому закону Кирхгофа равен сумме мгновенных значений фазных токов или геометрической сумме векторов фазных токов, или сумме комплексных фазных токов:
|
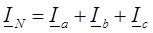. (9.6)
Рис.9.5. Векторная диаграмма напряжений и токов для равномерной активной нагрузки при симметричной системе питающих напряжений.
Положительные направления токов в линейных проводах выбраны от источника к приемнику, а в нейтральном проводе – от приемника к источнику. При равномерной активной нагрузке в фазах приемника, векторы фазных токов равны между собой по величине и совпадают по направлению с векторами фазных напряжений, образуя также симметричную звезду. Геометрическая сумма фазных токов в этом случае будет равна нулю (рис.9.5) и ток в нейтральном проводе протекать не будет.
. (9.7)
Отсюда можно сделать важный вывод о том, что при равномерной нагрузке (не только активной, но и любой) энергию от трехфазного источника к трехфазному приемнику можно передавать по трем проводам. Четвертый провод в этом случае не нужен, и от него можно отказаться. В результате этого достигается экономия материалов проводов и уменьшаются потери при передаче электрической энергии.
На рис.9.6 показана векторная диаграмма напряжений и токов для неравномерной активной нагрузки при симметричной системе питающих напряжений и при наличии нейтрального провода. Вектор тока в нейтральном проводе равен геометрической сумме векторов фазных токов. Чем больше несимметрия фазных токов, тем больше ток в нейтральном проводе. На практике стремятся загружать фазы приемника более или менее равномерно и тем самым уменьшать ток в нейтральном проводе до минимума. В связи с этим сечение нейтрального провода берется в 2-3 раза меньше, чем сечение линейных проводов.
В трехпроводной системе (т.е. без нейтрального провода (рис.9.2, в) сумма фазных, а, следовательно, и линейных токов всегда равна нулю, т.е.:
и 
. (9.8)
При равномерной нагрузке отсутствие нулевого провода не повлияет на работу системы. Если же нагрузка будет неравномерной и в фазах приемника будут протекать разные токи, то между нейтральными точками источника питания N и приемника n возникает напряжение 
. Это соответствует на векторной диаграмме смещению точки n относительно точки N (рис.9.7). Напряжение называют напряжением смещения нейтрали. Напряжение смещения нейтрали при отсутствии нейтрального провода определяют по формуле:
|
. (9.9)
Рис.9.6. Векторная диаграмма напряжений и токов для неравномерной активной нагрузки при симметричной системе питающих напряжений и при наличии нейтрального провода
Из формулы (9.9) следует, что напряжение смещения нейтрали будет изменяться при изменении нагрузки в любой фазе приемника. Напряжения на фазах приемника Ua,Ub,Uc в этом случае будут отличаться от фазных напряжений источника питания U A; U B; U C и определяться по формулам:
; 
; 
. (9.10)
Фазные токи определяются (рис.9.7):
; 
; 
. (9.11)
Из формул (9.10) и (9.11) следует, что вместе с изменением напряжения смещения нейтрали будут изменяться напряжения и токи в фазах приемника. Таким образом, при изменении нагрузки в одной фазе будут изменяться напряжения и токи в других фазах. Ввиду этого трехпроводная система при неравномерной нагрузке, соединенной звездой не применяется.
|
Рис.9.7. Векторная диаграмма напряжений и токов для неравномерной нагрузки в фазах приемника при отсутствии нейтрального провода.
Обрыв нейтрального провода при неодинаковой нагрузке фаз приемника вызывает изменение фазных напряжений: повышение на одних фазах приемников и понижение на других. Такое изменение недопустимо при осветительной нагрузке. Пониженное напряжение на фазах вызовет недостаточный накал ламп и они будут гореть тускло. Повышение напряжения на других фазах вызовет перекал и быстрое перегорание ламп. Неблагоприятно сказывается отклонение фазного напряжения от номинального значения и на других потребителях электрической энергии. Ввиду изложенного в нейтральный провод не ставят предохранители.
|
Рис. 9.8. Мгновенные мощности в фазах и суммарная мгновенная мощность в трехфазной системе при симметричной нагрузке.
|
Рис.9.9.. Мгновенные мощности в фазах и суммарная мгновенная мощность в трехфазной системе при несимметричной нагрузке.
Активная мощность трехфазной цепи определяется суммой активных мощностей фаз:
(9.12)
При равномерной нагрузке:
. (9.13)
Следует отметить, что при равномерной нагрузке активная мощность системы постоянная, т.е. не изменяется во времени (рис.2.9.8). Если же нагрузка по фазам неравномерная, то наряду с постоянной составляющей появляется пульсирующая составляющая, причем, чем больше неравномерность нагрузки, тем больше пульсации (рис.9.9).