Показания всех приборов записать в таблицу 9-2.
Таблица 9.2
| № п/п | Измерено | Вычислено | Примечание | ||||||||||
| I a | I b | I c | I N | U a | U b | U c | U Л | P a | P b | P c | P | ||
| А | А | А | А | В | В | В | В | Вт | Вт | Вт | Вт | ||
| R a = R b = R c | |||||||||||||
| R a ≠ R b ≠ R c | |||||||||||||
| R a=¥, R b¹ R c |
Формулы для расчетов те же, что и в п.1. На основании показаний приборов убедиться, что при наличии нейтрального провода в любых режимах:
; 
.
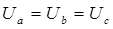3. Результаты расчетов (табл.9.2) при равномерной нагрузке и минимальных сопротивлениях (п.2.а) занести сначала для проверки в таблицу 9.3 в компьютере (вызвав ее из меню), а затем в такую же таблицу в отчете;
Таблица 9.3
| Ya | Yb | Yc | Pa | Pb | Pc | P |
| Cм | См | См | Вт | Вт | Вт | Вт |
4.Построить векторные топографические диаграммы напряжений и векторные диаграммы токов для всех случаев таблиц 9-1 и 9-2.
|
Рис.9.12. Построение векторной диаграммы напряжений при неравномерной нагрузке фаз и отсутствии нейтрального провода.
Методика построения векторной диаграммы напряжений при неравномерной нагрузке фаз и отсутствии нейтрального провода. Для случая трехпроводной системы при несимметричной нагрузке векторы фазных напряжений 
в нагрузке находятся следующим образом. Сначала строят симметричный треугольник линейных напряжений источника питания. Затем находят центр тяжести этого треугольника, который будет нейтральной точкой N источника питания (рис.9.12). Далее из вершины A,a проводят с помощью циркуля дугу радиусом, равным в масштабе напряжению 
фазы a. Затем с помощью циркуля из вершины B,b делают на дуге засечку радиусом, равным в масштабе напряжению 
. После этого из вершины C,c на первой дуге делают засечку радиусом, равным в масштабе напряжению 
. Все три дуги должны пересечься в одной точке, соответствующей нейтральной точке n приемника. Вектор, соединяющий точки N и n, соответствует вектору 
смещения нейтрали. Далее строят векторы фазных напряжений приемника, соединяя точку n и вершины треугольника линейных напряжений.
|
|
Контрольные вопросы
1. Определить показания вольтметров при включении обмоток трехфазного симметричного генератора по схемам, показанным на рис.9.13. Считать, что векторы фазной ЭДС направлены во всех фазах от конца обмотки к началу, равны по величине E =220В и сдвинуты по фазе на угол 120о.
Рис.9.13. Различные способы соединения обмоток трехфазного генератора.
2. Определить показание вольтметра на схеме на рис.9.14, если UЛ =380В и все сопротивления одинаковые.
Рис.9.14. К определению напряжения вольтметра.
3. Каковы соотношения между линейными и фазными напряжениями и токами при соединении симметричной трехфазной цепи звездой?
4. Как рассчитать симметричную трехфазную систему, соединенную звездой:
а) с нейтральным проводом;
б) без нейтрального провода.
5. Чему равен ток в нейтральном проводе:
а) при симметричной нагрузке
б) при несимметричной нагрузке.
6. Почему в схеме “звезда с нейтральным проводом” при несимметричной нагрузке, система напряжений на нагрузке остается симметричной?
|
|
7. Записать выражение для напряжения 
между нейтральными точками генератора и нагрузки.
8. Как выражается напряжение на фазах нагрузки через фазные напряжения генератора и .
9. Будут ли изменяться токи в фазах b и c при изменении нагрузки в фазе a в схеме «звезда с нейтральным проводом».
10.
|
Рис.9.15. Трехфазная система при соединении звездой.
11. В цепи, изображенной на рис.9.15, известны: ЕА=ЕВ=ЕС =127 В, R a=Rb=Rc =10 Ом. Какой ток течет в фазе генератора?
12.Начертить векторные диаграммы напряжений и токов при коротком замыкании фазы b при отсутствии нейтрального провода.
13.Начертить векторные диаграммы напряжений и токов при обрыве фазы a и при наличии нейтрального провода.
14.Начертить векторные диаграммы напряжений и токов при обрыве фазы a и при отсутствии нейтрального провода.