Направления скоростей и ускорений точек звеньев механизма

Структурное исследование плоского механизма

Вариант № 1.2

 

Рисунок 1.1 – Структурная схема механизма к варианту № 1.2

 

Исходные данные

Обозначение	Величина
LOA, м	0,25
LАВ, м	1,22
LВС, м	0,32
LАС, м	1,25
LСD, м	1,20
LЕD, м	0,70
LЕF, м	0,55
La, м	0,58
Lb, м	2,32
Lc, м	0,90
Ld, м	0,95
m, мм
Угол поворота начального звена (кривошипа ОА) α, град
Число оборотов ведомого вала n вд, об/мин

 

Структурная схема механизма в заданном положении показана на рисунке 1.2.

Рисунок 1.2 – Структурная схема механизма в заданном положении

 

Анализ кинематических пар представлен в таблице 1.1.

Таблица 1.1 – Анализ кинематических пар механизма

Номера пар п/п	Звенья, образующие пару	Относительное движение звеньев, допускаемое парой	Класс пары	Высшая или низшая пара	Наименование пары
Ι	0-1	Вращательное	II	Н	ВП
ΙΙ	1-2	Вращательное	II	Н	ВП
ΙΙΙ	2-3	Вращательное	II	Н	ВП
IV	3-4	Поступательное	II	Н	ПП
V	2-5	Вращательное	II	Н	ВП
VI	5-6	Вращательное	II	Н	ВП
VII	6-7	Вращательное	II	Н	ВП
VIII	6-8	Вращательное	II	Н	ВП
IX	8-9	Поступательное	II	Н	ПП
X	9-10	Вращательное	II	Н	ВП

 

Анализ звеньев механизма представлен в таблице 1.2.

 

Таблица 1.2 – Анализ звеньев механизма

Номера звеньев п/п	В какие пары входит звено	Абсолютное движение звена (относительно стойки)
	I	Неподвижно
	I, II	Вращательное
	II, III, V	Вращательно-поступательное
	III, IV	Поступательное
	IV	Неподвижно
	V,VI	Вращательное
	VI, VII, VIII	Вращательное
	VII	Неподвижно
	VIII, IX	Вращательно-поступательное
	IX, X	Вращательное
	X	Неподвижно

 

Число степеней подвижности механизма W по структурной формуле Чебышева:

(1.1)

где:

n – число звеньев механизма (включая стойку);

Р ₂ – число пар ΙΙ класс;

Р ₁ – число пар Ι класса.

 

Разделим механизм на структурные группы Ассура и первичный механизм. По методике Ассура любой механизм (плоский или пространственный) можно разделить на первичный механизм и на отдельные однотипные части (структурные группы), состоящие из определенного числа звеньев и кинематических пар. Для заданной структурной схемы механизма структурные группы Ассура показаны на рисунке 1.3.

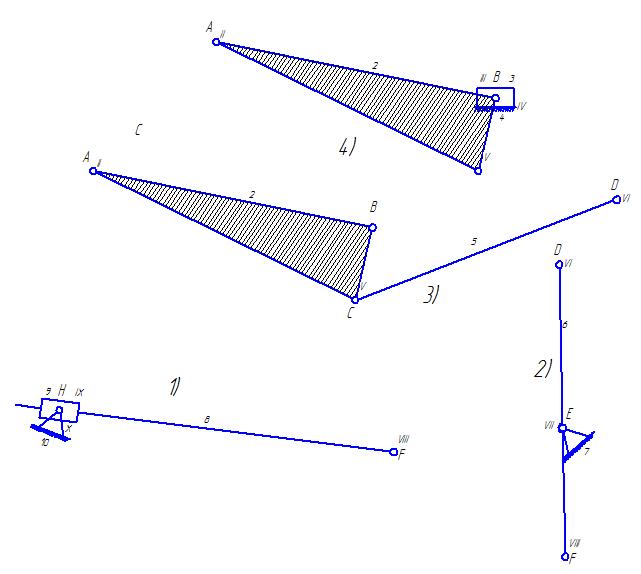
Рисунок 1.3 – Структурные группы Ассура

 

В таблице 1.3 представлено разделение механизма на структурные группы Ассура.

 

Таблица 1.3 – Структурные группы Ассура

№ группы в порядке ее отделения от механизма	Звенья, образующие группу	Внешние пары	Внутренние пары	Вид группы
	8,9	X, VIII	IX	3 (ВПВ)
	6,7	VIII, VI	VII	1 (ВВВ)
	2,5	VI, II	V	1 (ВВВ)
	2,3	II, IV	III	2 (ВВП)

 

Кинематический анализ плоского механизма

 

План положения механизма

 

Построение заданного положения механизма выполним в масштабе k_s=0,005 м/мм, тогда длины отрезков:

мм (2.1)

мм (2.2)

мм (2.3)

мм (2.4)

мм (2.5)

мм (2.6)

мм (2.7)

мм (2.8)

мм (2.9)

мм (2.10)

мм (2.11)

План положения механизма в соответствии с заданием показан на чертеже.

Планы скоростей и ускорений

 

Направления скоростей и ускорений точек звеньев механизма

 

В общем случае криволинейного движения вектор скорости точки А (рис 2.1, а), как и вектор тангенциальной составляющей полного ускорения, направлены по касательной к траектории движения, а вектор нормальной составляющей полного ускорения – вдоль нормали (отсюда название составляющей) к касательной по направлению к центру кривизны траектории О. В частном случае, когда траекторией является окружность, (рис. 2.1, б), то векторы и перпендикулярны радиусу ОА, а вектор направлен параллельно ОА от точки А к центру окружности О. В том случае, если ОА – звено механизма и известны его угловая скорость ω_ОА и угловое ускорение ε_ОА, то:

(2.12)

(2.13)

(2.14)

Вектор направлен в сторону вращения, т.е. совпадает с направлением угловой скорости ω_ОА. Направление вектора совпадает с направлением углового ускорения ε_ОА.

Если для любого звена построены план скоростей и план ускорений, то можно определить направления и величины угловой скорости и углового ускорения. Пусть для звена АВ (рисунок 2.2, а) построены план скоростей (рисунок 2.2, б) и план ускорений (рисунок 2.2, в) точек А и В.

 

Рисунок 2.1 – Направления скорости и ускорения криволинейного движения

Рисунок 2.2 – Определение угловой скорости и углового ускорения звена АВ

 

Перенесем в точку В звена вектор относительной скорости точки В, снятый с плана скоростей (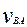 = k_{v *} аb) и вектор тангенциальной составляющей полного ускорения, снятый с плана ускорений ( = k_w nb '). Направления векторов и определят соответственно направления угловой скорости ω_АВ и углового ускорения ε_АB.

(2.15)

(2.16)