Определение скоростей и ускорений точек звеньев методом подобия

 

Угловая скорость кривошипа:

рад/с (2.17)

Масштаб плана скоростей:

(рад/с)/мм (2.18)

Масштаб плана ускорений:

(м/с²)/мм (2.19)

Скорость точки А:

рад/с (2.20)

Скорость (стойка неподвижна).

 

Вектор скорости точки А направлена в сторону вращения.

 

Определяем скорость точки B как векторную сумму скоростей переносного и относительного движений второго и третьего звена. Векторные уравнения можно записать так:

 

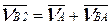(2.21)

(2.22)

(2.23)

Скорость точки А известна и по модулю и по направлению. Направление вектора относительной скорости перпендикулярно АВ. Вектор направлен вдоль прямой основания ОВ.

Через точку а плана скоростей проводим направление вектора перпендикулярно АВ.

Правая часть уравнения (2.23): поскольку первое слагаемое равно нулю, то построение начинаем от полюса, через который проводим направление вектора . Пересечение направляющих позволяет графически определить величины векторов и 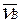в масштабе k_v.

Для нахождения скорости точки С строим треугольник ∆abc подобный ∆АВС на плане скоростей. Через полюс проводим прямую к точке с. Отрезок рс позволяет графически определить величину вектора в масштабе k_v. ас АС, вс ВС и обход (обозначения) вершин треугольников одинаков как по часовой так и против часовой стрелки.

Скорости точек структурной группы найдем по формулам:

м/с (2.24)

м/с (2.25)

м/с (2.26)

Угловая скорость звена 2:

рад/с (2.27)

 

 

Для определения скорости точки D воспользуемся выражениями:

(2.28)

(2.29)

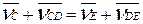(2.30)

Модуль и направление скорости точки С найдены, скорость точки Е (стойка не движется).

Через точку c плана скоростейпроводим направление вектора перпендикулярно DС; через полюс р проводим направление вектора перпендикулярно DE. Скорость точки D изображается отрезком рd.

Скорость точки F ₆ звена 6 определим методом подобия. Из пропорции

 

(2.31)

находим длину отрезка d f ₆ плана скоростей. Отрезок pf ₆ изображает вектор скорости точки F ₆ звена 6.

м/с (2.32)

м/с (2.33)

м/с (2.34)

м/с (2.35)

 

Угловая скорость звена 5:

рад/с (2.36)

Угловая скорость звена 6:

рад/с (2.37)

Точка F ₈ звена 8 совпадает с точкой F ₆ звена 6. Поэтому скорость равна найденной скорости . Скорость точки H равна нулю.

Cкорость точки H ₈ для данной структурной группы можно найти графически, зная что , а вектор взаимного вращательного движения направлен перпендикулярно HF. Из точки f ₈ строим направление вектора перпендикулярно HF. Через полюс проводим направление вектора параллельно HF. Пересечение направлений двух векторов – точка h ₈. Отрезок ph ₈изображает вектор искомой скорости .

м/с (2.38)

м/с (2.39)

Угловая скорость звена 8:

рад/с (2.40)

 

Поскольку ω ₁ = const, то:

м/с² (2.41)

От полюса р' откладываем отрезок р'a' = OA параллельно OA по направлению от точки A к точке O.

Ускорение точки A найдено, ускорение стойки равно нулю. Определяем ускорение точки B, для чего воспользуемся векторными уравнениями, выражающими ускорение точки B, как точки звена 2 (шатун AВС):

(2.42)

и как точки ползуна 3:

(2.43)

В уравнениях (2.42) и (2.43) известны: модуль и направление вектора ускорения точки А , ускорение неподвижной стойки = 0, модуль вектора нормального ускорения определяется графическим методом из пропорции:

(2.44)

Направление вектора параллельно АВ, направление вектора тангенциального ускорения перпендикулярно ВС. Модуль вектора ускорения Кориолиса определяется по формуле

(2.45)

где:

ω_ОВ – угловая скорость переносного движения, в данном случае направляющей стойки (ω_ОВ = 0);

– скорость относительного движения ползуна вдоль направляющей.

Тогда

(2.46)

Ускорение относительного движения ползуна параллельно направляющей стойке АС.

Объединяя уравнения (2.42) и (2.43) с учетом вышесказанного, получим:

(2.47)

Решаем векторное уравнение (2.47) графическим методом:

От точки а ' откладываем отрезок а ' n ₂ параллельно АВ по направлению от точки В к точке А. Через точку n ₂ проводим направление вектора перпендикулярно АВ.

Через полюс р' проводим направление вектора параллельно ОВ.

Точка в' пересечения направлений векторов и даст отрезок р'в', изображающий вектор абсолютного ускорения точки В.

Ускорение точки C определяем методом подобия, построив на отрезке a'b' плана ускорений ∆ a'b'c' подобный ∆ ABC. Как и на плане скоростей обход вершин треугольников должен быть одинаков в любом направлении.

м/с² (2.48)

м/с² (2.49)

м/с² (2.50)

м/с² (2.51)

Угловое ускорение звена 2 определяем по формуле:

с^-2 (2.52)

Направление ε ₂ совпадает с направлением вектора .

 

Ускорение точки С найдено. Ускорение стойки (точка Е) равно нулю. Ускорение точки D найдем из векторных уравнений:

(2.53)

(2.54)

(2.55)

Модули нормальных ускорений и определяем графическим методом. Отрезок c'n ₅, изображающий вектор , находим из пропорции:

(2.56)

Отрезок e'n ₅, изображающий вектор , – из пропорции:

(2.57)

Решаем векторное уравнение (2.55) графически.

От точки c' плана ускорений откладываем отрезок c'n ₅ параллельно DC по направлению от точки D к точке C. Через точку n ₅ проводим направление вектора перпендикулярно DC.

От полюса р' откладываем отрезок e'n ₆ параллельно DE по направлению от точки D к точке E. Через точку n ₆ проводим направление вектора .

Точка d' пересечения линий двух векторов даст отрезок р'd', изображающий вектор полного ускорения точки D.

Ускорение точки F ₆ звена 6 найдем методом подобия. Точка f' ₆ лежит на продолжении отрезка d'e', причем

(2.58)

Отрезок p'f ₆^' изображает вектор абсолютного ускорения точки F ₆ звена 6.

м/с² (2.59)

м/с² (2.60)

м/с² (2.61)

м/с² (2.62)

Угловые ускорения звеньев 5 и 6 совпадают по направлению с соответствующими тангенциальными ускорениями и и по величине равны:

с‾² (2.63)

с‾² (2.64)

Найдем ускорение точки H₈. Ускорение точки F известно по модулю и направлению, ускорение точки Н₉=Н₁₀=0 (опора неподвижна).

(2.65)

(2.66)

(2.67)

 

Отрезок e'n ₈, изображающий вектор по модулю и направлению определяется графически – из пропорции:

(2.68)

Аналогичным образом находим отрезок р'k изображающий вектор кориолисова ускорения из пропорции:

(2.69)

Через точку n₈ проводим направление вектора перпендикулярно HF.

Решаем уравнение (2.67) графически.

От f ₈ ' параллельно HF по направлению от точки F к точке H откладываем отрезок f ₈ 'n₈. Через точку n ₈ проводим направление вектора перпендикулярно HF.

Через полюс p' проводим направление вектора ускорения Кориолиса перпендикулярно HF и откладываем отрезок p’k затем через точку k проводим направление вектора параллельно FH.

Точка h'₈ пересечения направлений двух векторов даст отрезок , изображающий вектор абсолютного ускорения точки H8 звена 8.

м/с² (2.70)

м/с² (2.71)

Угловое ускорение звена 8:

с‾² (2.72)

Планы скоростей и ускорений показаны на чертеже.