Натяжение ведомой ветви цепной передачи можно принять равным  . Натяжение ведущей ветви цепной передачи
. Натяжение ведущей ветви цепной передачи
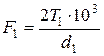 , Н (3.99)
, Н (3.99)
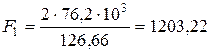 Н.
Н.
Передаваемое окружное усилие
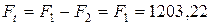 Н.
Н.
3.4.3 Проверка статистической прочности на разрыв
Предельная нагрузка, вызывающая разрыв цепи
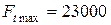 Н.
Н.
Поскольку выполняется неравенство
 Н,
Н,
то условие статической прочности на разрыв выполнено.
3.5 Проектировочный расчет клиноременной передачи
Исходные данные:
Определить основные геометрические размеры клиноременной передачи, предназначенной для передачи мощности  кВт.
кВт.
Частота вращения ведущего шкива  об/мин, передаточное число
об/мин, передаточное число  , величина межосевого расстояния
, величина межосевого расстояния 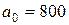 мм.
мм.
При работе передачи имеют место умеренные колебания нагрузки, пусковая нагрузка не превышает 150% от номинальной.
3.5.1 Выбор типа ремня
Проектировочный расчет выполняется для выбранного поперечного сечения ремня. Из таблицы 3.26 выбираем сечение 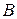 , для которого:
, для которого:
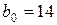 мм – ширина ремня на нейтральном слое;
мм – ширина ремня на нейтральном слое;
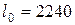 мм – длина эталонного ремня сечения
мм – длина эталонного ремня сечения  ;
;
 мм 2 – площадь поперечного сечения ремня;
мм 2 – площадь поперечного сечения ремня;
 мм – высота поперечного сечения ремня;
мм – высота поперечного сечения ремня;
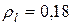 кг/м – масса единицы длины ремня (погонная плотность).
кг/м – масса единицы длины ремня (погонная плотность).
По таблице 3.27 определяем коэффициент динамичности нагрузки  . Для заданного характера нагрузки можно принять
. Для заданного характера нагрузки можно принять
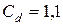 .
.
Момент вращения ведущего шкива
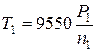 , Н м (3.100)
, Н м (3.100)
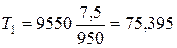 Н·м
Н·м
Таблица 3.26 - Основные размеры клиновых и поликлиновых ремней
| Тип ремня | Обозначение сечения | Размеры в сечении | 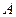 ,
см2 ,
см2
| 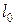
| 
| 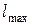
| 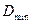
| 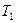
|  ,
кг/м ,
кг/м
| |||

| 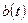
| 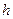
| 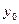
| |||||||||
| Клиновый нормального сечения | Z | 8,5 | 2,1 | 0,47 | <30 | 0,06 | ||||||
| A | 2,8 | 0,81 | 15-60 | 0,10 | ||||||||
| B | 10,5 | 4,0 | 1,38 | 45-150 | 0,18 | |||||||
| C | 13,5 | 4,8 | 2,30 | 120-600 | 0,30 | |||||||
| D | 6,9 | 4,76 | 420-400 | 0,62 | ||||||||
| E | 23,5 | 8,3 | 6,92 | 1600-6000 | 0,90 | |||||||
| Клиновый узкого сечения | SPZ | 8,5 | 2,0 | 0,56 | 0,07 | |||||||
| SPA | 2,8 | 0,95 | 90-400 | 0,12 | ||||||||
| SPB | 3,5 | 1,58 | 300-2000 | 0,20 | ||||||||
| SRC | 4,8 | 2,78 | >2000 | 0,37 | ||||||||
| Поликлиновый | К | - | 2,4 | 4,0 | - | 0,72 | 0,09 | |||||
| Л | - | 4,8 | 9,5 | - | 3,56 | 18-40 | 0,45 | |||||
| М | - | 9,5 | 16,7 | - | 11,37 | >130 | 1,6 | |||||
 - ширина ремня на нейтральном слое; - ширина ремня на нейтральном слое; 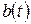 - ширина большего основания трапеции в сечении клинового ремня (шаг ребер поликлинового ремня); - ширина большего основания трапеции в сечении клинового ремня (шаг ребер поликлинового ремня);  - высота сечения ремня; - высота сечения ремня;  - площадь сечения; - площадь сечения; 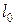 - длина стандартного ремня; - длина стандартного ремня;  - нижний предел длины; - нижний предел длины; 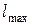 - верхний предел длины; - верхний предел длины;  - минимальный диаметр ведущего шкива; - минимальный диаметр ведущего шкива; 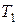 - вращающийся момент ведущего шкива; - вращающийся момент ведущего шкива;  - масса 1 м длины - масса 1 м длины
|
Для уменьшения геометрических размеров передачи в качестве диаметра малого шкива предварительно выбираем из таблицы 3.26 его минимальное значение,  мм, а затем в соответствии с нормальным рядом
мм, а затем в соответствии с нормальным рядом  округляем это значение до
округляем это значение до  мм.
мм.
Таблица 3.27 - Рекомендуемые значения
коэффициента динамичности нагрузки 
| Характер нагрузки | 
|
| Спокойная. Пусковая до 120% нормальной | |
| Умеренные колебания. Пусковая до 150% нормальной | 1,1÷1,2 |
| Значительные колебания. Пусковая до 200% нормальной | 1,25÷1,4 |
| Ударная. Пусковая до 300% нормальной | 1,5÷1,6 |
Рекомендованное значение коэффициента скольжения равно 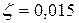 . Тогда диаметр ведущего шкива
. Тогда диаметр ведущего шкива 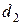
 , мм (3.101)
, мм (3.101)
 мм
мм
Полученное значение округляем до ближайшего из нормального ряда  ,
, 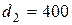 мм.
мм.
Определяем уточненное значение передаточного числа
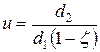 (3.102)
(3.102)

Расчетная длина ремня по заданному межосевому расстоянию
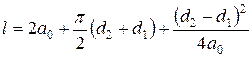 , мм (3.103)
, мм (3.103)
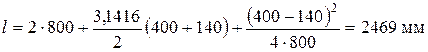
Окончательное значение длины ремня получаем, обратившись к нормальному ряду  :
:  мм. Далее уточняем величину межосевого расстояния
мм. Далее уточняем величину межосевого расстояния
 , мм (3.104)
, мм (3.104)
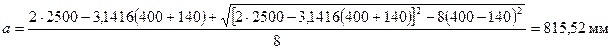
Для того чтобы принять окончательное решение по выбору величины межосевого расстояния, необходимо проверить выполнение следующего условия:
 ,
,
где граничные  и
и 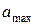 согласно существующим рекомендациям равны
согласно существующим рекомендациям равны
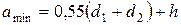 , мм (3.105)
, мм (3.105)
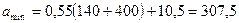 мм;
мм;
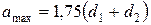 , мм (3.106)
, мм (3.106)
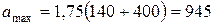 мм
мм
Поскольку полученная величина межосевого расстояния удовлетворяет предельным условиям, окончательно имеем
 мм.
мм.
Считая межосевое расстояние известным, рассчитываем номинальный угол обхвата малого шкива
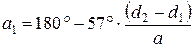 , (3.107)
, (3.107)
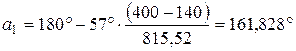
3.5.2 Расчет нагрузочной способности ременной передачи
Скорость перемещения ремня (3.23)
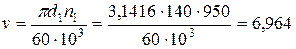 м/с.
м/с.
Определяем поправочный коэффициент 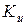 , который учитывает разные по величине напряжения изгиба на большом и малом шкивах
, который учитывает разные по величине напряжения изгиба на большом и малом шкивах
 (3.108)
(3.108)
 .
.
Приведенный диаметр шкива
 , мм (3.109)
, мм (3.109)
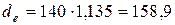 мм.
мм.
Число пробегов ремня в секунду:
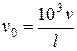 (3.110)
(3.110)
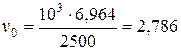
Полезное натяжение эталонного ремня
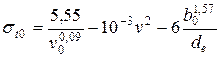 , МПа (3.111)
, МПа (3.111)
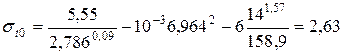 МПа.
МПа.
Поправочный коэффициент на угол обхвата ремня на малом шкиве
 (3.112)
(3.112)
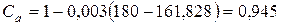
Поправочный коэффициент учета фактической длины ремня по отношению к эталонной
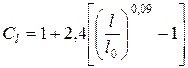 (3.113)
(3.113)
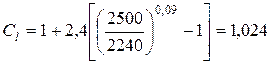
Допускаемая мощность, передаваемая одним ремнем для заданных условий эксплуатации в предположении равномерной нагруженности ремней
 , кВт (3.114)
, кВт (3.114)
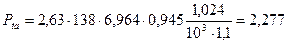 кВт.
кВт.
Необходимое количество ремней передачи
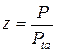 (3.115)
(3.115)

Поскольку количество ремней может быть только целым числом, полагаем 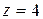 .
.
На практике ремни испытывают неодинаковую нагрузку. Это учитывается коэффициентом неравномерности нагрузки по потокам
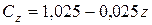 (3.116)
(3.116)
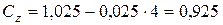 .
.
Мощность, передаваемая одним ремнем с учетом неравномерности нагрузки по ремням
 , кВт (3.117)
, кВт (3.117)
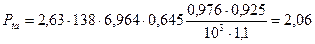 кВт
кВт
Уточняем количество ремней
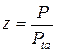 (3.118)
(3.118)
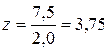 .
.
Окончательно принимаем 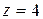 .
.
3.5.3 Расчет силовых параметров передачи
Полезное окружное усилие, передаваемое ременной передачей
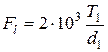 , Н (3.119)
, Н (3.119)
 Н.
Н.
Вспомогательный коэффициент  .
.
Натяжение ведущей ветви ремня
 , Н (3.120)
, Н (3.120)
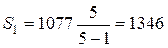 Н.
Н.
Натяжение ведомой ветви ремня
 , Н (3.121)
, Н (3.121)
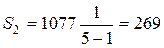 Н.
Н.
Напряжение ремня, возникающее при действии центробежной нагрузки
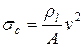 , МПа (3.122)
, МПа (3.122)
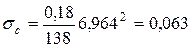 МПа.
МПа.
Дополнительное натяжение от центробежной нагрузки:
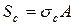 , Н (3.123)
, Н (3.123)
 Н.
Н.
Вычисления показывают, что центробежной нагрузкой, вследствие ее малости относительно сил натяжения, можно пренебречь.
Сила предварительного натяжения
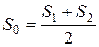 , Н (3.124)
, Н (3.124)
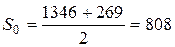 Н.
Н.
Напряжение в ремне от предварительного натяжения
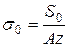 , МПа (3.125)
, МПа (3.125)
 МПа.
МПа.
Сила, действующая на вал со стороны шкива
 , Н (3.126)
, Н (3.126)
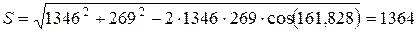 Н.
Н.
4 Расчет валов редуктора
4.1 Нагрузки, приложенные к валам
Детали, размещенные на валах, как правило, находятся под воздействием сосредоточенных или распределенных сил, а также изгибающих и крутящих моментов, которые деформируют вал и вызывают внутри него появление напряжений. Так как при статических расчетах приходится оперировать моделями, то размещенные на валу детали заменяются системой реактивных сил и моментов.
Опорами валов служат подшипники. Нагрузки в виде системы сосредоточенных и распределенных сил, а также изгибающих и крутящих моментов, должны быть приложены к геометрической оси вала. С этой целью силовые факторы переносятся из точек их фактического приложения в точки, лежащие на оси вала, известными методами механики. Реакция подшипника на вал представляется в виде сосредоточенной силы, точка приложения которой лежит в месте пересечения нормали в контакте тела качения с дорожкой в оси вала. Если реакция, действующая на вал со стороны подшипника, распределена вдоль шейки вала по некоторому закону, то точка приложения реакции является точкой приложения результирующей.
Обычно внешние нагрузки, приложенные к валу, не лежат в одной плоскости, вот почему их следует представлять в виде проекций на два взаимно перпендикулярных направления. Выполнив необходимые расчеты для каждой из двух взаимно перпендикулярных плоскостей, окончательный результат можно получить геометрическим сложением составляющих.
Внешние нагрузки вызывают в сечении вала нормальные и касательные напряжения. Нормальные напряжения возникают вследствие изгибающего момента, а касательные – как из-за наличия момента кручения, так и из-за поперечных сил. Последним видом напряжений, в силу их малости, обычно пренебрегают.
4.2 Предварительный расчет валов
Для валов (рис. 4.1) используем сталь 40Х (ГОСТ 4543-80) с термическим улучшением: закалка с высоким отпуском. Данный материал в сочетании с термическим улучшением обеспечивает следующие свойства:  МПа;
МПа; 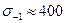 МПа;
МПа; 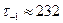 МПа;
МПа; 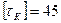 МПа.
МПа.

Рисунок 4.1 – Кинематическая схема привода
Предварительный расчет диаметров выходных концов валов осуществляем из расчета на кручение по формулам:
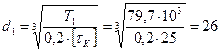 мм, по ГОСТ 6636-69 принимаем 30мм;
мм, по ГОСТ 6636-69 принимаем 30мм;
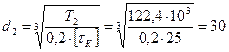 мм, по ГОСТ 6636-69 принимаем 30мм:
мм, по ГОСТ 6636-69 принимаем 30мм:
 мм, по ГОСТ 6636-69 принимаем 45мм;
мм, по ГОСТ 6636-69 принимаем 45мм;
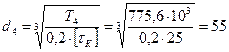 мм, по ГОСТ 6636-69 принимаем 55мм.
мм, по ГОСТ 6636-69 принимаем 55мм.
Диаметры остальных участков валов назначаем, исходя из конструктивных соображений при компоновке редуктора.
4.3 Проверочный расчет валов
Первый вал.
- крутящий момент на валу 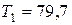 Н·м;
Н·м;
- делительный диаметр шестерни 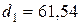 мм;
мм;
-окружная сила  H;
H;
- радиальная сила 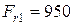 H;
H;
- осевая сила 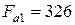 H.
H.
Строим эпюры изгибающих моментов в горизонтальной плоскости.
Определяем опорные реакции.
Силовые реакции опор определяем из условия уравновешенности моментов в горизонтальной и вертикальной плоскости относительно каждой из опор.
 Н
Н
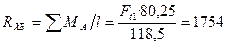 Н
Н
- проверяем правильность определенных реакций
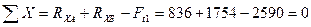 .
.
- строим эпюры изгибающих моментов 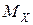 , для чего определяем их значение в характерных сечениях вала:
, для чего определяем их значение в характерных сечениях вала:
 Н·м;
Н·м;
 Н·м.
Н·м.
В вертикальной плоскости:
 Н
Н
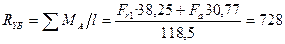 Н
Н
Проверяем правильность определенных реакций:
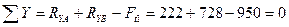
- строим эпюры изгибающих моментов 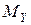 , для чего определяем их значение в характерных сечениях вала:
, для чего определяем их значение в характерных сечениях вала:
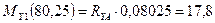 Н·м;
Н·м;
 Н·м.
Н·м.
Строим эпюру крутящих моментов (рис. 4.2). Крутящий момент, передаваемый вдоль вала от середины ступицы муфты до середины первой шестерни равен  Н·м.
Н·м.
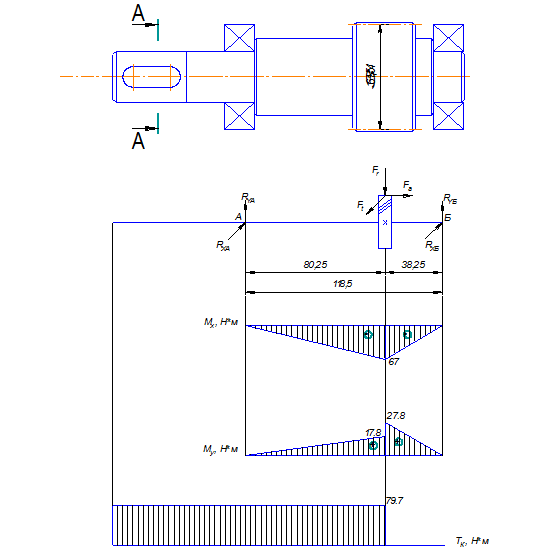
Рисунок 4.2 - Расчетная схема 1-го вала
Уточненный расчет состоит в определении коэффициентов запаса прочности 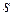 для опасных сечений и сравнении их с требуемыми (допускаемыми) значениями.
для опасных сечений и сравнении их с требуемыми (допускаемыми) значениями.
В соответствии с формой вала и эпюрами 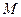 и
и 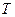 предположительно опасными сечениями вала, подлежащими проверке на усталостную прочность, являются сечения А-А, Б-Б, В-В, Г-Г, в которых имеются концентраторы напряжений и возникают наибольшие моменты.
предположительно опасными сечениями вала, подлежащими проверке на усталостную прочность, являются сечения А-А, Б-Б, В-В, Г-Г, в которых имеются концентраторы напряжений и возникают наибольшие моменты.
Определяем запас усталостной прочности в сильно нагруженном сечении А – А, в котором концентрация напряжений обусловлена шпоночной канавкой.
Коэффициент запаса прочности по напряжениям кручения определятся по формуле:
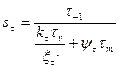 , (4.1)
, (4.1)
где 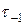 – предел выносливости при кручении;
– предел выносливости при кручении;
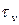 ,
,  – соответственно амплитуда и среднее значение напряжения отнулевого цикла;
– соответственно амплитуда и среднее значение напряжения отнулевого цикла;
 – коэффициент концентрации напряжений кручения, принимаем для шпоночного участка вала
– коэффициент концентрации напряжений кручения, принимаем для шпоночного участка вала 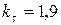 ;
;
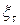 – масштабные факторы, принимаем
– масштабные факторы, принимаем 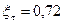 ;
;
 – коэффициент влияния среднего напряжения цикла на усталостную прочность, для легированных сталей
– коэффициент влияния среднего напряжения цикла на усталостную прочность, для легированных сталей  .
.
Осевой момент сопротивления:
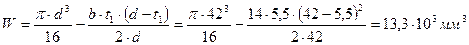 .
.
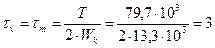 .
.
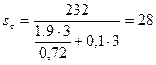 .
.
Коэффициент запаса прочности по нормальным напряжениям определяем аналогично:
 (4.2)
(4.2)
где 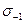 – предел выносливости при изгибе;
– предел выносливости при изгибе;
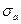 ,
, 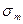 – соответственно амплитуда переменных напряжений и среднее значение напряжения цикла (Учитывая характер работы вала, можно, если противное не обговорено особо, закон изменения вызванных изгибом нормальных напряжений считать симметричным, а сжатием и растяжением по отношению к изгибу пренебречь. При таких допущениях
– соответственно амплитуда переменных напряжений и среднее значение напряжения цикла (Учитывая характер работы вала, можно, если противное не обговорено особо, закон изменения вызванных изгибом нормальных напряжений считать симметричным, а сжатием и растяжением по отношению к изгибу пренебречь. При таких допущениях 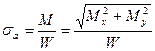 ,
, 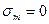 . Учитывая силу и момент от муфты для нашего сечения А-А,
. Учитывая силу и момент от муфты для нашего сечения А-А, 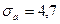
 );
);
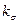 – коэффициент концентрации напряжений изгиба, принимаем для шпоночного участка вала
– коэффициент концентрации напряжений изгиба, принимаем для шпоночного участка вала 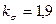 ;
;
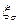 – масштабные факторы, принимаем
– масштабные факторы, принимаем  ;
;
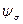 – коэффициент асимметрии цикла, учитывающий влияние средних напряжений на величину усталостной прочности,
– коэффициент асимметрии цикла, учитывающий влияние средних напряжений на величину усталостной прочности, 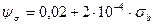 .
.
