Ю.П.Головатый
Статистический анализ результатов измерений
Методические указания к лабораторной работе №4
по «Основам проектирования наноприборов и систем на их основе»
Калуга
2013 г.
УДК 621.382
Данные методические указания издаются в соответствии с учебным планом специальности 152200.62
Указания рассмотрены и одобрены: кафедрой «Материаловедение»
Протокол №_________ от _______________
Заведующий кафедрой ____________________ В.Г.Косушкин
Методической комиссией Калужского филиала
Протокол №__________от ________________
Председатель Методической
комиссии _______________ М.Ю. Адкин
Рецензент: д.т.н., профессор кафедры ФН2-КФ
________________
Автор: ст. преподаватель _______________ Ю.П. Головатый
Аннотация.
В данной лабораторной работе рассмотрены методы численного решения нелинейных уравнений. Основное внимание уделено наиболее распространенному методу Ньютона-Рафсона.
© Калужский филиал МГТУ им. Н. Э. Баумана, 2013 г.
© Головатый Ю.П.
Оглавление
1. Цель работы.
2. Основные понятия статистики
3. Построение плотности распределения результатов измерений
4. Оценка точности технологических процессов
5. Порядок выполнения работы
Цель работы.
Цель работы: освоить методы статистического анализа результатов измерений в научных исследованиях и в целях контроля технологии производства наноприборов
Основные понятия статистики.
Статистический анализ - это сравнение, сопоставление, изучение рядов однородных эмпирических цифровых данных с целью установления взаимосвязей и закономерностей, характеризующих явления и процессы.
Ряды эмпирические цифровых данных появляются в результате многократных однотипных измерений. Такие измерения типичны в научной и инженерной деятельности.
В научных исследованиях измерения никогда не бывают абсолютно точными. Это значит, что мы верим в то, что измеряемая величина 
имеет истинное числовое значение 
, но узнать его не можем из-за неизбежных ошибок измерений. Измеренное значение 
отличается от истинного значения на величину ошибки 
.
Ошибки измерений имеют двоякое происхождение. Во-первых, их вносит любой измерительный прибор. Приборная ошибка называется погрешностью. Во-вторых, ошибки вносят неконтролируемые случайные внешние факторы – колебания электрического напряжения в сети, вибрации, освещение, температура, флюктуации физических величин.
Если погрешность прибора больше случайных ошибок, то любые два измерения дадут различные результаты. Тогда возникает задача об определении значения измеряемой величины, наиболее близкого к истинному значению, по выборке из 
результатов измерений.
Если же погрешность прибора меньше случайных ошибок, то любые два измерения дадут одинаковые результаты. Измерения с помощью достаточно грубых приборов применяются при контроле качества продукции. Цель контроля качества - избежать отклонений параметров изделия от заданных значений на величину, превышающую допуск. Отклонения в этом случае могут происходить из-за нарушения технологических режимов. Статистический анализ позволяет своевременно выявить такие отклонения и принять меры к их устранению.
Распределение результатов измерений принято описывать функцией плотности распределения вероятности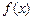 
. Смысл ее в том, что 
дает долю 
от полного числа N результатов измерений, попадающих в интервал от x до 
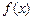. почти всегда имеет вид кривой с максимумом (рис.1)
Рис.1 Возможный вид плотности вероятности результатов измерений
По определению, 
(1)
Среднее значение величины x для данного распределения определяется соотношением
(2)
Оно есть обобщение обычного определения среднего арифметического значения. Если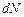 
измерений дают значение , то
Среднее значение величины принимается за ее истинное значение,
(3)
Дисперсия распределения 
определяется соотношением
(4)
а 
(5)
называется среднеквадратичным (стандартным) отклонением.
Среднее значение и стандартное отклонение – важнейшие параметры распределения. Они могут быть вычислены, если известна функция плотности распределения вероятности .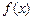
Вид функции плотности распределения вероятности определяется характером процессов, приводящих к разбросу результатов измерений.
Чаше других в физике и технике используется гауссово или нормальное распределение
(6)
Оно задается двумя независимыми параметрами и 
, совпадающими с истинным (наиболее вероятным) значением величины x и её среднеквадратичным отклонением. В (6) и неизвестны, поэтому их оценивают приближенно через среднее арифметическое значение
(7)
и выборочное (стандартное) отклонение
(8)
Наряду с плотностью распределения вероятности 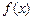в статистике важное значение имеет функция распределения 
, определяемая соотношением
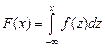(9)
Она выражается через интеграл вероятности 
,
(10)
Графики функци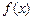й и показаны на рис.2 для 
, 
Рис.2 Гауссово (нормальное) распределение
для случая x0 = 2, σ = 0,5.
Функция распределения дает вероятность попадания отдельного измерения в интервал 
. Вероятность попадания результата измерения в интервал [ x1,x2 ] равна
(11)
Величину P, выраженную в процентах, называют статистической достоверностью. Она имеет следующие значения для характерных интервалов:
, 
, 
, 
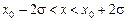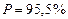
Таким образом, за пределами интервала 
около среднего значения остается только приблизительно одна четырехсотая часть всех измерений.
Широкое применение гауссова распределения обусловлено тем, что, с одной стороны, оно очень удобно, а, с другой – считается, что оно описывает плотность вероятности для многих физических величин при их измерениях. Широко известный пример – рассеяние пуль при стрельбе или радиальное распределение частиц в электронных, протонных и фотонных пучках. Его можно обосновать теоретически при некоторых предположениях о вероятностях исходов измерений, но лучше всего о применимости этого распределения сказано словами: экспериментаторы верят в него, полагаясь на доказательства математиков, а математики – полагаясь на экспериментальное обоснование.
Построение плотности распределения результатов измерений
Приближённое представление о плотности распределения даёт гистограмма – столбчатый график, показывающий частоту появления результата измерения в определенном интервале значений.
Для построения гистограммы надо разбить интервал 
, охватывающий все результаты измерений, на некоторое число 
одинаковых подинтервалов 
, и подсчитать число 
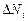результатов измерений, попадающих в 
-й подинтервал 
, 
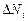. есть частота попадания результата измерения в подинтервал 
. Относительные частоты 
откладываются в виде столбиков высотой 
в центре каждого подинтервала. Это и есть гистограмма.
Огибающая гистограммы даёт представление о плотности распределения вероятности результатов измерений.
В большинстве случаев предполагается, что огибающая суть гауссова кривая (6). Если гистограмма сильно отличается от гауссианы, это свидетельствует о влиянии на измерения некоторых неслучайых факторов.