План:
1. Функция распределения системы, ограниченной воображаемыми стенками.
2. Большой канонический формализм.
3. Термодинамическая интерпретация распределений Гиббса.
1. Рассмотрим построение термодинамического формализма, связанного с выделением термодинамической системы с помощью воображаемых стенок (
). Несмотря на то, что определение химического потенциала представляется весьма сложной задачей (эта величина непосредственно не измеряется, а вычисляется на основе косвенных измерений, причем, достаточно сложным образом), отказ от точной фиксации числа частиц существенно упрощает рассмотрение ряда задач.
Очевидно, что рассмотренная ранее фиксация числа частиц N с точностью до 1 шт. носит идеализированный характер и по большому счету представляет формальный прием, облегчающий анализ. В действительности же не только не только энергия, но и число частиц оказываются размыты о числу частиц 
около среднего значения 
. Как и для разброса 
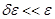, разброс захватывает сравнительно большое число частиц (
).
Полагая далее, что система выделена с помощью воображаемых стенок и число N не может быть включено в число переменных состояния системы, воспользуемся сопряженной к 
величиной – химическим потенциалом 
. Поскольку величина внутренней энергии 
также зависит от числа частиц ее необходимо заменить на величину 
(см. тему №3)
Тогда II-е начало термодинамики для квазистатических процессов, имеющее вид:
(7.1а)
преобразуется к виду:
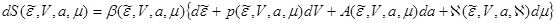(7.1б)
Найдем функцию распределения 
по микроскопическим состояниям термодинамической системы. Очевидно, эта функция должна удовлетворять ряду требований:
1. Распределение 
должно определять вероятность обнаружить систему в состоянии с заданными значениями N и n. Здесь N – число частиц в системе (с точностью до 1 штуки), 
- набор квантовых чисел, определяющих микроскопическое состояние системы N тел.
|
|
2. Желательно, чтобы в качестве макроскопических переменных, описывающих состояние термодинамической системы, использовались величины (
).
3. Полученное распределение должно быть сосредоточенным около значения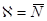 
по числу частиц N и около значения по энергии.
Сформулированное требование позволяет использовать закономерности и допущения, положенные в основу микроканонического и канонического распределений.
Очевидно, величина при фиксированном представляет среднее значение микроскопических характеристик 
. Тогда, учитывая сформулированную выше аксиому о равновероятности микросостояний, соответствующих заданному макросостоянию, выражение для распределения по микроскопическим состояниям , можно записать, по аналогии с микроскопическим распределением Гиббса (5.12):
. (7.2)
Здесь 
- сосредоточенная около нуля квазикронекоровская функция (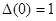
), 
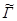- нормировочная сумма (аналог статистического веса):
(7.3)
Как известно, основная асимптотика статистического веса Г при 
не зависит от выбора типа стенок, ограничивающих термодинамическую систему. То есть она не зависит от выбора набора макроскопических параметров: (), (
), (
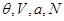) и т.д., фиксирующих равновесное состояние системы. Тогда введенная величина 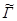и связанная с ней 
по сути являются статистическим весом Г и энергией S термодинамической системы
Учитывая (6.8), представляющей явное выражение функции 
, перепишем (7.2) в виде:
|
|
При записи (7.4) было использовано выражение (3.21) для термодинамического потенциала “омега” 
.
Найдем выражение для нормировочной суммы 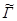, подставляя в (7.3) выражение (6.8) для функции :
Поскольку, согласно (5.11) 
получим:
(7.5)
Для дальнейшего анализа разложим энтропию 
в степенной ряд по отношению числа частиц N от среднего термодинамического значения 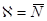, ограничиваясь членами второго порядка. При этом учтем: 
(см. ф-лу (3.28)). Тогда получим:
Подставляя полученный результат в (7.5), находим:
Учитывая большое число частиц N и, пологая 
, перейдем от суммирования в последнем выражении к интегралу. Получаем:
(7.6)
Вычислим интеграл в полученном равенстве:
Подставляя полученный результат в (7.6), получаем:
Тогда вычисляя в обеих частях последнего равенства предел при и отбрасывая в правой части сомножители, растущие медленнее, чем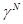 
, получаем:
(7.6)
Подставляя (7.6) в (7.4), находим:
(7.7)
Выражение (7.7) получило название большого канонического распределения Гиббса. Включая в себя каноническое распределение (6.15) как частный случай, это распределение также содержит распределение по числу частиц. Если 
, то (7.7) принимает вид (6.15).
Нормировочная сумма:
(7.8)
получила название большой статистической сумы. Эта величина связана с термодинамическим потенциалом 
посредством соотношения:
(7.9)
При необходимости, используя аппарат макроскопической термодинамики можно осуществить в (7.8) переход к другим переменным. Покажем, что на примере перехода от () и (). Из (7.1) следует:
или 
и т.д.
Полученные равенства можно рассматривать как термодинамические уравнения относительно химического потенциала, решением которых будет выражение 
. А учитывая (3.21): 
, можно исключить и переменную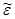 
, выражая ее в виде 
. Тогда для энтропии и, соответственно статистического веса, можно записать:
|
|
(7.10)
Аналогичным образом осуществляется пересчет и для других переменных состояния и параметров термодинамической системы.
Как и в рассмотренном ранее каноническом распределении, для большого канонического распределения можно показать, что является чрезвычайно сосредоточенным распределением как по числу частиц N, так и по энергии Е.
Воспользуемся аналогией с выполненным в предыдущей теме расчетом ширины канонического распределения по энергии. Тогда ширина распределения по N рассчитывается на основе дисперсии 
и оказывается равной
(7.11)
Здесь 
- макроскопические усреднения концентрации частиц.
Тогда для относительной флуктуации 
числа частиц, получаем:
(7.12)
Таким образом, допустимые большим каноническим распределением состояния с числом частиц N сосредоточены в узком интервале значений вблизи точки . Ширина этого интервала в предельном статистическом случае стремится к нулю по закону 
. Несложно получить и вид распределения по числу частиц. Выполняя ту же последовательность действий, что и в предыдущей теме для получения распределения по энергии 
, приходим к следующему распределению:
(7.13)
Легко видеть, что (7.13) с математической точки зрения представляет распределение Гаусса с математическим ожиданием и дисперсией 
.
Кроме того, большое математическое распределение может быть использовано для определения дисперсии энергии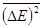 
. Используя соотношение 
, проводя непосредственные вычислении и учитывая (6.19), в итоге получим:
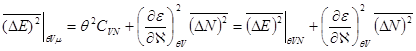(7.14)
2. Введеный в предыдущем вопросе большой канонический формализм Гиббса представляет собой замкнутый аппарат равновесной статистической механики.
Запишем алгоритм проведения конкретных расчетов с использованием большого канонического распределения:
1. Ищется решение уравнения Шредингера для каждого значения N в пределах 
:
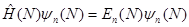(7.15)
2. Осуществляется вычисление в главной по V (или по 
) асимптотике большой кинетической суммы:
(7.16)
Зная явный вид выражения (7.16), могут быть вычислены термодинамический потенциал “омега” и все термодинамические характеристики системы:
и т.д.
Заметим, что все термодинамические характеристики задаются в переменных (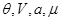
).
Кроме того, может быть найдено большое каноническое распределение
Это распределение позволяет рассчитать средние значения любых динамических величин, дисперсии флуктуации (при фиксированных 
) и т.д.
В случае необходимости, которая, как правило, возникает, производится пересчет полученных результатов от переменных (
) к переменным (
), который производится на термодинамическом уровне. Уравнение
разрешается относительно 
.
Это позволяет исключить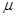 
из результатов, полученных в пункте 2. Например,
Заметим, что процедура пересчета результатов в других переменных может быть осуществлено и при вычислении статистических сумм.
3. Подведем итог полученным результатам в соответствии с различными способами выделения термодинамической системы из окружения. То есть фактически приведем общую структуру равновесной статистической механики, которая нами была построена, применительно к различным способам термодинамического описания систем многих частиц:
1) Система с адиабатическими стенками. В этом случае фиксируются параметры (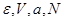
). Функция распределения Wn, определяющая структуру смешанного состояния, выражается при помощи микроканонического распределения Гиббса:
,
а аналитический вес
связан с макроскопической характеристикой – энтропией:
,
которая является термодинамическим потенциалом для переменных состояния (
).
Такое представление имеет преимущественно общетеоретический интерес, поскольку на его основе четко просматриваются основные постулаты и ограничения. На основе которых осуществляется построение статистической механики.
2) Система в термостате, 
- состояние задается параметрами (). Функция распределения Wn задается каноническим распределением Гиббса:
Статистическая сумма
связана с макроскопическим параметром – свободной энергией
,
являющейся термодинамическим потенциалом в переменных ().
3) Система, выделенная с помощью воображаемых стенок. Выбранный способ описания очень удобен и широко используется, особенно в статистической механике классических систем. В этом случае фиксированными оказываются параметры (), а число частиц N оказывается микроскопическим параметром. В этом случае функция распределения 
вводится с помощью большого канонического распределения Гиббса:
Для выбранного способа описания связь с макроскопическими характеристиками системы осуществляется посредством большой статистической суммы:
Соответствующим термодинамическим потенциалом является потенциал 
:
,
который и является термодинамическим потенциалом для системы с воображаемыми стенками.
Этот способ описания также широко используется. Наиболее удобным оказалось использование этого способа в квантовой статистической механике. Относительное неудобство большого канонического формализма связано с часто возникающей необходимостью пересчета результатов к более удобным параметрам ().
4) Система под поршнем. В этом случае фиксируются параметры (
), а объем V рассматривается в качестве микроскопического параметра. Тогда функция распределения 
, задающая структуру смешанного состояния, имеет вид:
Здесь 
- “гибсовская” статистическая сумма, равная:
и связанная с термодинамическим потенциалом Гиббса:
,
характеризующим систему, заданную в переменных (
).
Этот подход также оказывается удобным при рассмотрении некоторых частных задач.
В случае необходимости состояние термодинамической системы может быть описано и с помощью другого набора параметров. Тогда необходимо ввести соответствующие функции распределения и статистические суммы, связав последние с соответствующим термодинамическим потенциалом. Выбор конкретного способа описания не влияет на окончательный результат, однако способен существенно упростить или усложнить процесс исследования термодинамической системы. Это относится как к точным, так и к приближенным методам.