Описание исходных данных и метод их получения.
Исходным данными для расчета АСР является две разгонные характеристики получения на объекте.
W – по главному каналу и
W1 – по вспомогательному каналу.
Изобразим структурную схему комбинированной АСР Na – катионитового фильтра
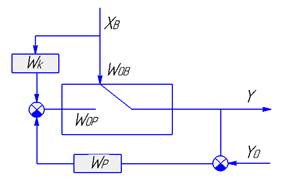
Структурная схема комбинированной АСР фильтра
Структурная схема показывает наличие двух каналов воздействия на выходную координату объекта и исполнением двух контуров регулирования замкнутого и параллельного.
Преобразуем схему

Динамические характеристики объекта, то есть Na катионитового фильтра по каналам возмущения и регулирования списываются передаточным функциями:
 |
Рассчитаем подстройки в одноконтурной АСР
Методом РАФХ
Цель расчета: найти параметры подстроек Sr Sn Sy которые обеспечат устойчивый переходной процесс.
Описание используемого метода расчета
Дана передаточная функция:
Необходимо найти SР Sи Sg 

 |
В основу метода положен критерии обеспечивающий заданную степень затухания переходного процесса.
 |
 |
m=0.221 и

Амплитудно-фазовую характеристику можно представить виде:
 |
где 1+Wоб (jw)*R(jw)=0

P= -mw+jw

 |
 |  | ||
Для того чтобы сделать расчет настроек, надо определить расширенный модуль А(w), φ(w). Re(w). Jm(w)
Re левой стороны = Re правой стороны и Jm лев= Jm прав.
Тогда левая сторона управления приобретает вид:

где γ = w·(1+m2), m.c.
 |  |
правая часть рассматривается:
 |  | ||

 |
Подставим, данные значения получим:

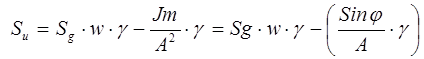
Для ПИ: Sg=0
ПИД: Sg=10,20,100.
Ход расчета
| w | Re(w) | Jm(w) | модуль | Фаза (град) | Фаза (рад) |
| 0,050 | 0,206626 | -0,396004 | 0,0446623 | -62,45671 | -1,09006 |
| 0,075 | -0,005224 | -0,369485 | 0,369503 | -90,810089 | -1,58493 |
| 0,100 | -0,123961 | -0,262975 | 0,290726 | -115,238342 | -2,01129 |
| -0,125 | -0,160573 | -0,157320 | 0,224796 | -135,586349 | -2,36643 |
| -0,150 | -0,155 | -0,80495 | 0,174641 | -152,564896 | -2,66276 |
| 0,175 | -0,1344191 | -0,030913 | 0,137705 | -167,027313 | -2,91518 |
| 0,200 | -0,110539 | -0,000641 | 0,110341 | -180 | -3,15579 |
По полученным данным найдем параметры
Настроек: для ПИ:Sg=0. тo
где:


m2=0.048841
1. γ = 0,052442 Sp= - 0,5971221 Su = 0,1041108
2. γ = 0,078663 Sp= 0,6363332 Su = 0,2128776
3. γ = 0,1048841 Sp= 2,1542232 Su = 0,4079111
4. γ = 0,1311051 Sp= 3,8655913 Su = 0,4081554
5. γ = 0,1573261 Sp= 5,6653344 Su = 0,415218
6. γ = 0,1835471 Sp= 7,4368862 Su = 0,2992132
7. γ = 0,2097682 Sp= 9,0578511 Su = 0,0109989
Для ПИД:
 |
 |
При S·g = 10; Sg = 10
1. Sp= - 0,3181221 Su = 0,0978858
2. Sp= 0,9648332 Su = 0,2638804
3. Sp= 2,7122232 Su = 0,503027
4. Sp= 5,3130913 Su = 0,5442741
5. Sp= 6,0023344 Su = 0,6742289
6. Sp= 8,6633862 Su = 0,6219922
7. Sp= 9,9738511 Su = 0,4085375
Sg=20
1. Sp= 1,0391221 Su= 0,0916688
2. Sp= 1,2366668 Su= 0,3348631
3. Sp= 3,2702232 Su= 0,55981429
4. Sp= 4,9605913 Su= 0,8803927
5. Sp= 4,3393344 Su= 0,8867603
6. Sp= 5,8898862 Su= 0,9431996
7. Sp= 7,2898511 Su= 0,8280739
Sg = 100
1. Sp= 2,8071221 S4= 0,3580992
2. Sp= 3,6786668 S4= 0,8770949
3. Sp= 7,2657768 S4= 1,6409299
4. Sp= 9,6594087 S4= 2,2306583
5. Sp= 12,2646656 S4= 2,9446735
6. Sp= 16,2981138 S4= 3,512859
7. Sp= 18,2178511 S4= 4,1843651
Рассчитаем настройки в комбинированной АСР.
Цель расчета: необходимо найти параметры настроек Sp, S4 ; выбрать компенсатор и определить его параметры из условия инвариантности на нулевой и рабочих частотах.
Описание используемого метода расчета: Даны передаточные функции
W – по главному каналу
W1 – по вспомогательному каналу
 |
Нужно найти Sp и S4
Рассмотрим условия инвариантности разомкнутой системы:
y (t) = 0

Структурная схема разомкнутой АСР.
Переходя к изображениям по Лапласу Хв(p) Х(р) сигналов Хв(t) и y(t), и принимаем это условие с учетом передаточных функции объекта по каналам возмущение Wв(p) и регулирования Wp(p) и компенсатора R
Х(p): Y(p) = Хв(р) · [Wв (p)+Rx(p)·W(p)]=0
При помощи возмущения [Xв(р) не равно 0] условие инвариантности выполняются если:
Wв(p)+Rх(р)·Wp(P)=0; откуда
Rк(p) = - Wв(р) / Wp(P)
Таким образом, для обеспечения инвариантности системы регулирования по отношению к какому либо возмущению необходимо установить динамический компенсатор, передаточная функция которого равна отношению передаточных функции объекта по каналам возмущения и регулирования, взятому с обратным знаком.
Выведем условие инвариантности для комбинированной АСР. Сигнал от компенсатора подается на вход объекта, Na-катионитового фильтра. Структурная схема комбинированной АСР преобразуется к последовательному соединению разомкнутой системы и замкнутого контура передаточной функции, которые соответственно равны:
Wps(P) = Wв(p)+Rк(p)·Wp(P)
 |
При этом условии инвариантности записывается в виде
 |
Если Хв(p) не равно 0 и W3c(p) не равно 0, должно выполнятся условие:
Wpc(P)=Wв(В)+Rк (P)·Wp(P)=0
т.е условие инвариантности.
Настройки регулятора считают обычным способом (метод Циглера-Никольса)
Физическая реализуемость компенсаторов имеет два условия:
1. Компенсатор не должен содержать звено с отрицательным чистым
запаздыванием, т.е. время чистого запаздывания, т.е. время чистого запаздывания по каналу регулирования должно быть не больше, чем по каналу возмущения. С учетом до 1827 время чистого запаздывания компенсатора τк=τв-τр>0.
2. Компенсатор не должен содержать дифференцирующие звенья.
Компенсатор выбирает из числа наиболее легко реагируемых динамических звеньев, параметры которых рассчитывают из условие близости частотных характеристик идеального и реагентного компенсаторов в этом диапазоне частот
Wк (w) = Wк (w); wж < w < w*
Диапазон [ wж, w* ] зависит от частичного спектра сигнала возмущения и частотных характеристик системы.
Расчет комбинированной АСР включает следующие этапы:
1. расчет настроек регулятора и определение рабочей частоты в замкнутой системе регулирования;
2. вывод передаточной функции идеального компенсатора и анализ его реализуемости;
3. выбор структуры реального компенсатора и определение его параметров из условия инвариантности на нулевой и рабочих частотах.
Ход расчета
Динамические характеристики объекта по каналом возмущения и регулирования описывается передаточными функциями:
 |
 |
В комбинированной АСР используется П- регулятор с передаточной функцией;
R(p) = -S1
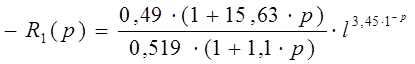
Определим настройки регулятора по методу Циглера-Никольса. Из системы управлении Ар(w)·S1=1; φn (w) + π = 0
где
φ
 |
p(w) = -1,30w -аrctd·w

 |
Re=1; Jm=1,1w;
φ
 |
p(w) = -1,30w - arctd 1,1W
где wкр= 0,2; S1кр = 9,0464171;
Так как компенсатор с передаточной функцией не содержит звеньев с отрицательным чистым запаздыванием, идеальный компенсатор физически реализации.
Для выбора типа реального компенсатора, найдем частичные характеристики идеального компенсатора в диапазоне частот [0…wp]
Амплитудно-частотная характеристика
 |
Фазо-частотная характеристика
φк(w)= -3,45w + аrctd 15,63w – arctd
При w = 0; w = 0,2
Aк(0) = 0,94; φк(0)=0
Ак(0,2) = 3,0130755; φк(0,2) = - 0,957
 |
Так как в интервале W [0; 0,2] Rк (w) проходит в четвертом квадрате, в количестве апериодического звена 1-го порядка.
 |  | ||
Рис. ФИХ реального компенсатора Рис. АФХ реального компенсатора
 |
Rk = Ak (0) = 0,94
- arctd 0,2T = - 0,937
Система управлений апериодического звена 1-го порядка.
 |
φ (w) = - arctd T·w уравнение не имеет точного решения.
Т = 0,08285; φk (0,2) = - 0,94; Ak(0,2) = 3,02
 |
 |
 |
 |  | ||||
 | |||||
Графики переходных процессов АСР для одноконтурной и комбинированной.
Анализ расчетов АСР показал, что рабочие частоты регуляторов в комбинированной АСР незначительно отличаются от соответствующих частот в одноконтурной системе регулирования.
Окончательный вывод об эффективности применение комбинированной АСР по сравнению с одноконтурной можно сделать на основе сравнительного анализа результатов моделирования переходных процессов.
Как видно из сравнения кривых динамическая ошибка регулирования в комбинированной АСР снизились почти в два раза.