Лекция 16 Основные методы интегрирования (2ч)
Содержание лекции: Основные методы интегрирования: непосредственное интегрирование; замена переменной (метод подстановки); интегрирование по частям.
Проинтегрировать функцию – значит, найти хотя бы одну ее первообразную. Рассмотрим основные методы интегрирования, которые позволяют преобразовывать данный интеграл и цель этих преобразований – привести данную задачу интегрирования, сразу или через несколько шагов, к одной или нескольким табличным формулам. Существует несколько методов интегрирования:
I. непосредственное интегрирование;
II. замена переменных;
III.интегрирование по частям.
Рассмотрим каждый из них.
Метод непосредственного интегрирования
Под непосредственным интегрированием будем понимать приведение заданного интеграла к одному или нескольким табличным с помощью тождественных преобразований подынтегрального выражения и свойств неопределенного интеграла. Рассмотренные в предыдущей лекции примеры демонстрировали применение тождественных преобразований и свойства линейности для приведения заданного интеграла к нескольким табличным.
Рассмотрим особо применение свойства 6 к вычислению неопределенного интеграла:
если 
, то 
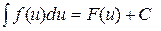для любой дифференцируемой функции и = и (х).
Это свойство позволяет значительно расширить таблицу простейших интегралов, так как в силу его все формулы таблицы справедливы не только для независимой переменной х, но и в случае, когда х – дифференцируемая функция какой-либо другой переменной.
Например,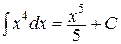 
, но и 
, и 
.
Или 
и 
, 
.
В рассмотренных интегралах , , подынтегральная функция есть сложная функция некоторой переменной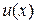 
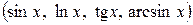, и под знаком дифференциала стоит эта же функция 
. При этом каждый из интегралов, на основании свойства 6, является табличным. В некоторых случаях в заданном подынтегральном выражении удается сформировать дифференциал некоторой функции 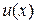так, чтобы этот дифференциал в совокупности с остальным выражением составляли табличную формула относительно функции 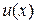. Такой прием называется подведением под знак дифференциала. При этом используется тот факт, что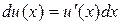 
|
|
Рассмотрим примеры.
Пример2.
а) 
;
б) 
.
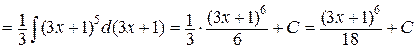в) 
(в последнем примере записано ln(3 + x 2) вместо ln|3 + x 2|, так как выражение 3 + x 2 всегда положительно).
Выведем несколько дополнительных формул, которые наряду с табличными желательно запомнить.
,
,
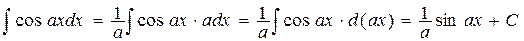замена переменных в неопределенном интеграле (метод подстановки).
Только что рассмотренный прием подведения под знак дифференциала является частным случаем метода замены переменных и используется, в основном, тогда, когда в подынтегральном выражении легко выделить дифференциал некоторой функции и «узнать» в получившемся после выделения дифференциала выражении табличный интеграл относительно этой функции. Если же в уме подобные преобразования произвести трудно, используют замену переменных. Суть метода в следующем.
Пусть требуется вычислить интеграл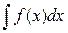 
, но непосредственно подобрать первообразную для f (x) не удается, хотя известно, что она существует. Заменим переменную интегрирования, положив х = j(t), где j(t) непрерывная функция, имеющая обратную t = j–1(x), тогда dх = j¢(t) dt и имеет место равенство
= 
,
|
|
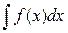где g (t) = f (j(t))j¢(t).
Если для функции g (t) первообразную найти нетрудно и она равна G (t), то согласно свойству 6, имеем
= 
.
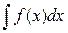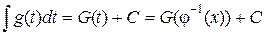Рассмотрим примеры.
Пример3.
.
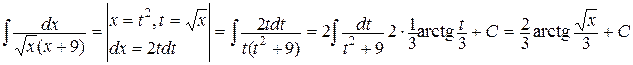При интегрировании методом замены переменных иногда удобнее подбирать подстановку в виде t = j(x), но при этом необходимо, чтобы в заданном подынтегральном выражении f (x) dx можно было легко получить множитель вида j¢(x) dx, дающий дифференциал новой переменной t.
Пример4.
а)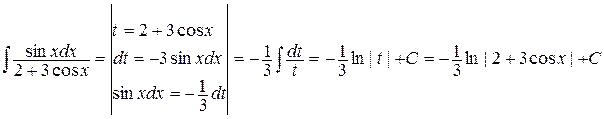 
.
Заметим, что этот интеграл можно вычислить и подведением под знак дифференциала, если учесть, что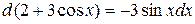 
.
б) 
.
Выбор правильной подстановки зависит от навыка и интуиции вычислителя. Если выбор окажется не совсем удачным, замену переменных можно применять несколько раз, пока не будет получен результат. В некоторых часто встречающихся ситуациях можно дать определенные рекомендации (здесь и в дальнейшем буквой R будем обозначать рациональную функцию соответствующих аргументов):
– используется подстановка t = ex
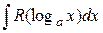– используется подстановка t = log ax.
В дальнейшем мы рассмотрим еще некоторые классы интегралов, в которых используются вполне конкретные подстановки.