Проведем сравнительный анализ поверхностей разрушения, полученных по критериям Мора, Лебедева–Писаренко и деформационному критерию для пластичного (титановый сплав ВТ2-0) и хрупкого (инструментальная сталь ШХ15) материалов, представленных на рисунках 6 и 7.
Рисунок 6. Поверхности разрушения, построенные для хрупкого материала –
инструментальной стали ШХ15 – по трем критериям прочности
Рисунок 7. Поверхности разрушения, построенные для пластичного материала –
титанового сплава ВТ2-0– по трем критериям прочности
В случае хрупкого материала критерий Лебедева – Писаренко проходит через все характерные точки, отвечающие шестиугольнику Мора.
В первом квадранте построенных в относительных координатах 
поверхностей разрушения (область растягивающих напряжений – "жесткие" напряженные состояния) критерии Мора и Лебедева–Писаренко дают оценку не в запас прочности.
Введем параметр, характеризующий длину радиус-вектора точки, принадлежащей поверхности разрушения
.
Этот параметр соответствует длине луча, проведенного из начала отсчета в пространстве напряжений в точку на поверхности разрушения. Тогда, рассматривая отношения длин лучей (выбранного параметра l) соответствующих различным критериям, можно будет сравнить эти критерии между собой.
Таблица12. Значения длин радиус-векторов точек, принадлежащих поверхностям разрушения для хрупкого и пластичного материалов
| Вид напряженного состояния | Длина луча, l | |||||
| Титановый сплав ВТ2-0 | Инструментальная сталь ШХ15 | |||||
| Критерий О. Мора | Критерий Лебедева-Писаренко | Деформационный критерий | Критерий О. Мора | Критерий Лебедева-Писаренко | Деформационный критерий | |
| 1,414 | 1,414 | 1,171 | 1,414 | 1,414 | 0,985 |
| 1,118 | 1,214 | 1,124 | 1,118 | 1,196 | 0,991 |
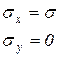
| 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 0,919 | 0,939 | 0,951 | 0,900 | 0,967 | 1,059 |
| 0,987 | 0,987 | 0,987 | 0,952 | 1,044 | 1,173 |
| 1,113 | 1,133 | 1,097 | 1,135 | 1,244 | 1,392 |
| 2,308 | 1,691 | 1,461 | 2,063 | 2,063 | 2,062 |
| 2,581 | 2,181 | 2,166 | 2,306 | 2,663 | 3,471 |
| 3,264 | 2,391 | 2,496 | 2,917 | 2,917 | 4,189 |
Анализируя данные таблицы 12 можно сказать о том, что при плоском равноосном растяжении критерии Мора и Лебедева-Писаренко дают одинаковые оценки разрушающего напряжения. В то же время, деформационный критерий дает оценку ниже на 21% для пластичного и на 37% для хрупкого материала. Исходя из экспериментальных данных, можно сказать, что оценки по критериям Мора и Лебедева-Писаренко идут не в запас прочности.
Во втором, третьем и четвертом квадрантах поверхностей разрушения хрупкого материала критерий Мора и Лебедева – Писаренко дают более консервативную оценку, чем наиболее адекватный деформационный критерий.
В третьем квадранте для пластичного материала критерий Мора дает завышенные оценки разрушающего напряжения. При плоском равноосном сжатии отличие между разрушающими напряжениями, определенными по деформационному критерию и по критерию Мора составляет 30% для титанового сплава ВТ2-0 и 44% для инструментальной стали ШХ15. Причем, если для пластичного материала величины разрушающих напряжений, определенные по деформационному критерию и критерию Лебедева - Писаренко, более консервативны чем оценка Мора, то в случае хрупкого материала оценка, полученная при помощи деформационного критерия значительно «мягче» чем результаты полученные критериями Мора и Лебедева-Писаренко.
Во втором и четвертом квадрантах максимальное отличие оценок по критериям Мора и Лебедева–Писаренко от оценки разрушающих напряжений, предсказываемой деформационным критерием, составляет 23 % для инструментальной стали ШХ15 (причем ошибка идет в запас прочности), для титанового сплава ВТ2-0 это отличие составляет 58 % (с ошибкой идущей не в запас прочности).
Следует отметить существование изломов на поверхности, построенной по критерию Лебедева-Писаренко, в точках, соответствующих одноосному сжатию, и приплюснутость поверхности в первом квадранте, построенной по деформационному критерию для хрупкого материала.