ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ
1. Рассмотрим движение двух тел, взаимодействующих друг с другом центральным образом, то есть
, (1)
где 
(по поводу обозначений см. задачу двух тел) и 
- произвольная функция. Такое поле является потенциальным; потенциальная энергия тел может быть определена как некоторая функция от относительного расстояния между взаимодействующими точками:
. (2)по поводу обозначений см. ствующих друг с другом центральным образом, то есть
Вообще говоря, формула (2) может считаться альтернативным определением центрального поля как поля, потенциальная энергия в котором зависит только от модуля радиус-вектора точки наблюдения. В дальнейшем будем обозначать 
.
Покажем, что из (2) следует центральность поля, выражаемая также условием (1). Имеем для связи силы и потенциальной энергии:
. (3)
Поскольку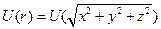 
, то
. (4)
Аналогично можно получить
, 
. (5)
Подставляя (4), (5) в (3), получим
,
то есть что сила коллинеарна вектору 
, соединяющему в нашем случае взаимодействующие точки. Напомним, что доказательство потенциальности поля центральных сил можно найти в стандартных курсах механики.
2. При движении в потенциальном поле точка сохраняет свою механическую энергию:
. (6)
Заметим, что, строго говоря, в этом выражении мы должны были писать приведенную массу 
. Отмечая это обстоятельство, в дальнейшем все же мы будем придерживаться стандартного обозначения массы как m, имея в виду, что в практически наиболее важных случаях 
и фактически совпадает с массой более легкого тела.
Покажем теперь, что, хотя тело и могло бы двигаться по трехмерной пространственной кривой, в действительности в поле центральных сил движение материальной точки происходит в неизменной плоскости. Для доказательства этого заметим, что, так как в центральном поле 
, то момент этой силы 
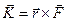относительно точки О начала координат 
равен нулю. Поскольку изменение момента импульса материальной точки описывается уравнением
, (7)
то 
влечет 
и 
. Надо особо отметить, что эта константа векторная и определяет (а) направление в пространстве и (б) плоскость, перпендикулярную этому направлению. Умножим теперь обе части уравнения
(8)
скалярно на радиус-вектор материальной точки. С одной стороны, имеем:
. (9)
(Тут без комментариев – ну что-то же вы должны соображать!)
С другой стороны, в силу предыдущего и (8): 
, то есть
. (10)
(10) означает перпендикулярность 
и . Поскольку отсчитывается от фиксированной точки О, это вектор всегда лежит в одной и той же плоскости, проходящей через начало отсчета О и нормальной к вектору (см. Рис. 1). В этой самой плоскости и лежит движение материальной точки в центральном поле.
Уфф! Устали! Передых.
Независимость
Притча неизвестного происхождения
Казалось, Мастера абсолютно не волнует впечатление, которое он производит на других людей.
Когда ученики спросили, как ему удалось достичь такого состояния внутренней свободы, он рассмеялся:
— До двадцати лет меня совсем не заботило мнение окружающих. После двадцати стало безразлично, что обо мне подумают. Но однажды — когда мне было за пятьдесят — я вдруг обнаружил, что на меня никто и не думал обращать внимание!
3. Введем в плоскости движения полярную систему координат 
с ортами 
(см. Рис. 2). Учтем, что, так как вектор скорости в этой системе
имеет компоненты 
, а базис ортонормирован, то 
. Тогда закон сохранения (6) механической энергии можно представить в виде:
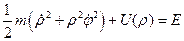. (11)
Далее, поскольку 
, а в цилиндрической системе координат с осью z, направленной по вектору , вектора имеют компоненты: 
, 
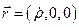(в последней формуле учтено, что движение происходит в плоскости z=0), уравнение сохранения момента импульса (8) может быть переписано в виде:
. (12)
Раскрывая определитель по второй строке, получим уравнение
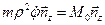, (13)
откуда и следует второе уравнение для определения движения точки в поле центральной силы:
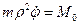. (14)
По своей сути это уравнение выражает закон сохранения момента импульса. Уравнения (11), (13) образуют систему уравнений относительно неизвестных функций 
:
,
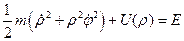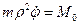. (15)
Формальное решение системы (15) достаточно просто. Выразим из ее второго уравнения 
: 
и подставим это выражение для в ее первое уравнение. В результате получим замкнутое уравнение относительно 
:
. (16)
Это уравнение имеет вид эффективного одномерного уравнения
, (17)
где эффективная потенциальная энергия 
определяется как
. (18)
«Эффективную потенциальную энергию» следует отличать от истинной потенциальной энергии: в (18) первое слагаемое справа не имеет материального источника в виде зарядов, тяготеющих масс и т. п. В структуре 
присутствует физически обусловленное слагаемое 
. Первое же слагаемое возникает из-за сведения изначально двумерного движения к одномерному, происходящего с изменением только координаты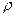 
. Иногда это нефизическое слагаемое называют «центробежной энергией». Терминология эта, однако, оправдана из-за сходства с одномерным уравнением движения в потенциальном поле:
. (19)
Общность формы уравнений (18), (19) диктует аналогичность их решения.
Действительно, как и при истинно одномерном движении, для решения (17) следует выразить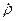 
как функцию :
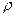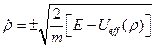. (20)
Здесь существенно удерживать оба знака, отвечающие двум ветвям движения: происходящим с увеличением 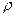(при 
), и происходящим с уменьшением 
(при 
). (20) решается разделением переменных
(21)
с последующим интегрированием:
. (22)
Константы 
и 
играют роль неопределенных постоянных. Далее, после интегрирования (исход которого весьма и весьма не гарантирован, как минимум, в терминах элементарных функций J) мы приходим к уравнению 
с формальным (и зачастую реально недостижимым) решением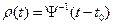 
. Нас, однако, не будут парить такие несущественные мелочи, как невозможность взять интеграл или решить аналитически какое-нибудь чудовищное трансцендентное уравнение. Будем выше этого и считать задачу решенной, если ее удалось довести хотя бы до квадратур, то есть свести проблему нахождения координат от времени к интегрированию, например, как в (22).
После определения 
появляется ранее не существовавшая возможность определить 
. С этой целью представим второе уравнение системы (15) как
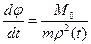. (23)
Поскольку к этому моменту функция уже известна, то (23) так же решается разделением переменных:
, (24)
. (25)
Формулы (22), (25) отвечают на вопрос о зависимости координат материальной точки от времени при ее движении в произвольном центральном поле.
4. Во многих случаях нас интересует не зависимость координат точки от времени, а форма траектории, ее замкнутость. Для ответа на такие вопросы рациональнее пользоваться уравнением, связывающим не время с координатами, а сами полярные координаты. Для получения такого уравнения используем уравнения (21) и (24):
,
. (26)
После почленного деления первого уравнения на второе получаем уравнение, в котором исключено время:
. (27)
Разделяя здесь переменные и интегрируя, получим
. (28)
Это уравнение определяет траекторию 
.
К этому вопросу прилегает частный вопрос о замкнутости траектории движения точки. Поскольку этот вопрос имеет смысл только для финитного по движения, то есть когда 
, где 
, 
- точки поворота, рассмотрим участок траектории между двумя соседними точками поворота (см. Рис. 3). Интегрируя (28) в пределах, соответствующих этим точкам, получим:
. (29)
Очевидно, при выполнении равенства
, (30)
где k, n – натуральные числа, траектория замкнется после n эволюций между точками поворота. Общий угол поворота при этом составит 
. Условия (29), (30) являются условиями замкнутости траектории. Поскольку им удовлетворить сложно, траектории в центральных полях оказываются замкнутыми только для ограниченного набора потенциальных полей. Например, замкнутые траектории возможны в полях с потенциальными энергиями 
(кулоновский потенциал), 
(осциллятор). Такт как потенциалы взаимодействия планет и Солнца имеют малые отличия от кулоновского, то траектории движения планет Солнечной системы оказываются незамкнутыми. Это приводит к известному эффекту смещения перигелия https://ru.wikipedia.org/wiki/%D0%A1%D0%BC%D0%B5%D1%89%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BF%D0%B5%D1%80%D0%B8%D0%B3%D0%B5%D0%BB%D0%B8%D1%8F_%D0%9C%D0%B5%D1%80%D0%BA%D1%83%D1%80%D0%B8%D1%8F
. Наиболее ярко он проявляется для ближайшей к Солнцу планеты (какой? Нибиру? J). Рис. 4 показывает примерный вид траектории этой планеты. Часть этого эффекта (примерно50%) обязана поправкам общей теории относительности, но половина все же имеет совершенно сермяжное объяснение.
Рис. 4
До сих пор нормален
Суфийская притча
Один учитель сетовал знакомому:
— Перевелись настоящие ученики! Мой первый ученик был слаб здоровьем, и упражнения свели его в могилу. Второй сошёл с ума — довёл себя своими медитациями. Третий совсем отупел от постоянного чтения священных книг. Только четвёртый ученик до сих пор остаётся нормальным, совершенно нормальным.
— Как ты думаешь, почему?
— Ну, — вздохнул учитель, — возможно, потому что отказывается выполнять те упражнения, которые я ему даю.