Санкт-Петербургский университет
Государственной противопожарной службы
МЧС России
Кафедра прикладной механики и инженерной графики
Утверждаю
Начальник кафедры
полковник внутренней службы
К.С. Иванов
«_____» ________________20__ года
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ДЛЯ ПРОВЕДЕНИЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ
По учебной дисциплине «Начертательная геометрия.
Инженерная графика»
для заочной формы обучения – 6 лет обучения
Раздел № 1. «Начертательная геометрия».
Тема № 2 «Проецирование точки и прямой линии».
Занятие № 1 «Проецирование точки и прямой линии».
Обсуждена на заседании кафедры
(предметно-методической секции)
Протокол №______от
«____»_______________20 _ года
Санкт-Петербург
20 _
I.Цели
1.Углубить и закрепить теоретические знания.
2.Привить практические навыки.
3.Проверить качество усвоения обучаемыми учебного материала.
4.Воспитывать стремление к углубленному освоению материала по теме занятия, обучению методам самостоятельной работы с первоисточниками и учебными материалами.
II. Расчет учебного времени
| Содержание и порядок проведения занятия | Время, мин. |
| ВВОДНАЯ ЧАСТЬ ОСНОВНАЯ ЧАСТЬ Учебные вопросы: 1. Точка. Способы задания точки на эпюре Монжа. Точки общего и частного положений. 2. Прямая линия. Задание прямой на эпюре Монжа. Прямые общего и частного положений. 3. Следы прямой. 4. Относительное положение прямых. ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ |
III. Учебно-методическое обеспечение
1. Демонстрационные плакаты, сборник ЕСКД.
IV.Методические рекомендации по подготовке и
Проведению практического занятия.
ВВОДНАЯ ЧАСТЬ.
Проверить наличие обучаемых, объявить тему, учебные цели и вопросы занятия, последовательность их отработки.
ОСНОВНАЯ ЧАСТЬ.
Точка. Способы задания точки на эпюре Монжа.
Точки общего и частного положений.
Точка является основным геометрическим элементом линий и поверхностей, поэтому базой для изучения прямоугольного проецирования предметов являются способы построения прямоугольных (ортогональных) проекций точки.
Ортогональными проекциями точки на плоскостях проекций являются основания перпендикуляров проведенных из заданной точки на эти плоскости (Рис. 1, а). При этом вдоль координатных осей XYZ определяются соответственно абсцисса, ордината и аппликата точки. Задание координат точки обычно осуществляется в форме, например, А (5,10,7), где цифры: первая – абсцисса X, вторая – ордината Y, третья – аппликата Z.

|
Точка и ее проекции обозначаются буквами латинского алфавита или цифрами. Точка в пространстве обозначается прописными буквами (на рисунке – А) или римскими цифрами (I, II,…).
Рис. 1
Проекции точки на плоскостях проекций обозначаются строчными буквами или арабскими цифрами: на горизонтальной плоскости Н без штриха (а), на фронтальной плоскости V со штрихом (а’), на профильной плоскости W с двумя штрихами (a’’). От каждой проекции точки проводятся линии проекционной связи, перпендикулярные к осям координат. Точка пересечения линий проекционной связи с осями координат обозначаются строчными буквами с индексами, указывающими соответствующую ось координат (ах, ау, аz). После совмещения плоскостей проекций Н, V и W в одну плоскость путем их поворота вокруг осей координат осуществляется переход к ортогональной системе проекций, которая называется эпюром (рис.1, б).
На эпюре горизонтальная а и фронтальная а’, а также профильная а’’ проекции точки А связываются линиями проекционной связи,, перпендикулярными соответственно осям координат X и Z.
Следует подчеркнуть, что если заданы, например, горизонтальная а и фронтальная а’ проекции точки А, то ее профильная проекция а’’ определяется однозначно путем несложного геометрического построения, приведенного на рис. 1, б. При этом перенос точки ау с одной полуоси Y на другую может быть осуществлен одним из трех равнозначных способов, приведенных на рисунке.
Таким образом, точка в пространстве может быть однозначно задана двумя ее ортогональными проекциями, по которым геометрически можно при необходимости построить третью ее проекцию. Поэтому на эпюре точка, как правило, задается только двумя проекциями, например, горизонтальной а и фронтальной а’ (рис. 1, в).
Точки в пространстве могут размещаться различным образом. В связи с этим различают точки общего положения, если они не находятся ни на плоскостях проекций, ни на координатных осях и точки частного положения, если они лежат на плоскостях проекций или на координатных осях. Для того, чтобы определить, в каком октанте находится или иная точка общего положения можно воспользоваться данными табл. 1.
Таблица 1.
| Октанты | Знаки координат | ||
| X | Y | Z | |
| I. | + | + | + |
| II. | + | - | + |
| III. | + | - | - |
| IV. | + | + | - |
| V. | - | + | + |
| VI. | - | - | + |
| VII. | - | - | - |
| VIII. | - | + | - |

Размещение точек частного положения также определяется их координатами. Если точка находится на плоскости проекций, то ее координата по координатной оси, перпендикулярной этой плоскости, должна быть равна нулю, например,точка А (5,10,0) будет находиться на горизонтальной плоскости проекций.
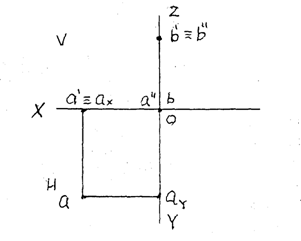
Если точка частного положения находится на координатной оси, то ее координата по этой оси не равна нулю, а по другим координатным осям координаты точки должны равняться нулю. Например, точка В (0,0,5) будет находится на оси Z.
Пример 1.
 А (6, 0, 3)
А (6, 0, 3)
(-yH) X
Точка А – точка частного положения, принадлежит плоскости V. Ее проекции лежат на осях проекций X и Z: а на Х и а// на Z.
Пример 2.
|
 V
V
X
-YW