Лекция 6.
(с.)
Второй метод Ляпунова.
Пусть непрерывная эволюционная система описывается системой обыкновенных дифференциальных уравнений, записанных в нормальной форме:
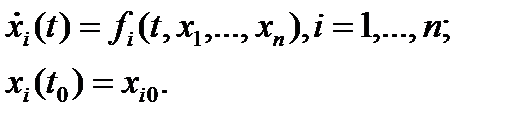(0)
Здесь 
- независимая переменная, обычно называемая временем; 
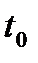- искомые функции, 
и 
- заданные начальные условия, а символ 
обозначает производную функции 
. Функции 
предполагаются вещественными.
Универсальным методом исследования устойчивости различных классов систем является второй метод Ляпунова. В качестве инструмента исследования во втором методе используются некоторые специальные функции, называемые функциями Ляпунова.
Рисунок 1. Примерный вид функции Ляпунова
Рисунок 2. Поверхности уровня функции Ляпунова
Вещественную непрерывно дифференцируемую функцию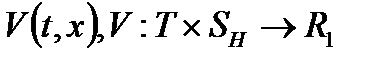 
, удовлетворяющую условию 
, называют функцией Ляпунова. Примерный вид функции Ляпунова двух переменных 
и ее поверхности уровня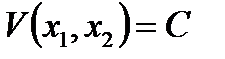 
изображены на рис. 1 и 2. Назовем производной 
функции 
в силу уравнения (0) величину:
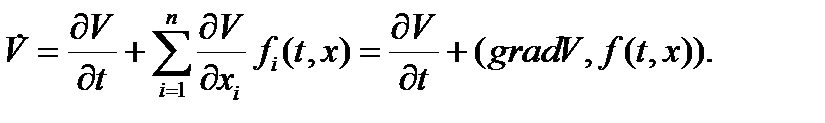(1)
Если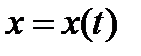 
есть решение уравнения (0), то представляет собой полную производную по времени сложной функции 
. Отметим, что для вычисления фактического знания решения 
не требуется.
Всюду в дальнейшем через 
обозначены скалярные непрерывные неубывающие функции такие, что 
и 
при 
(рис. 3).
Теорема 1 (первая теорема Ляпунова). Пусть существует функция Ляпунова 
такая, что
(2)
(3)
Тогда тривиальное решение уравнения (0) устойчиво по Ляпунову.
□ Возьмем любое 
и любое 
. В качестве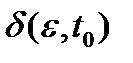 
выберем такое число, что
Из непрерывности функции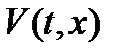 
и условия 
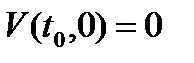следует, что такое 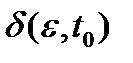обязательно найдется (рис. 4). Условие (3) означает, что функция не возрастает вдоль решений уравнения (0). Используя неравенства (2) и (3), при 
и 
получим
В силу монотонности 
отсюда вытекает, что 
.■
Рисунок 3. Вид функции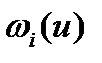 
Рисунок 4. Иллюстрация теоремы Ляпунова об устойчивости
Функции 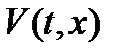, удовлетворяющие условию (2), называются определенно-положительными. Сам Ляпунов использовал другое, эквивалентное (2) определение таких функций. Производная 
, удовлетворяющая условию (3), называется знакоотрицательной.
Теорема 2 (К.П. Персидский). Если в дополнение к условиям теоремы 1 справедливо неравенство
(4)
то тривиальное решение уравнения (0) равномерно устойчиво по начальному моменту 
.
□По заданному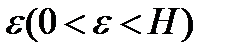 
определим число 
(
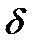не зависит от 
) таким образом, что 
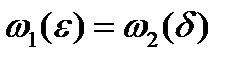. Используя (2) – (4) и монотонность 
, при 
и 
получим
.
В силу монотонности 
отсюда следует, что 
.■
Про функции Ляпунова, удовлетворяющие условию (4), говорят, что они допускают бесконечно малый высший предел.
Теорема 3 (вторая теорема Ляпунова). Пусть существует функция Ляпунова 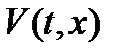такая, что
, (5)
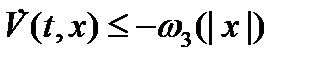. (6)
Тогда тривиальное решение уравнения (0) равномерно асимптотически устойчиво.
□ B силу теоремы Персидского решение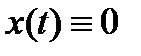 
равномерно устойчиво. Покажем, что второе условие определения также выполнено. Возьмем 
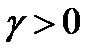и определим 
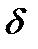из соотношения 
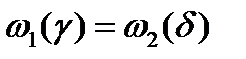. B качестве 
возьмем число 
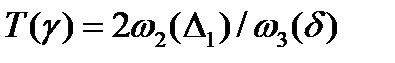. На отрезке 
найдется момент 
такой, что 
и 
при 
. Если это не так, то получим
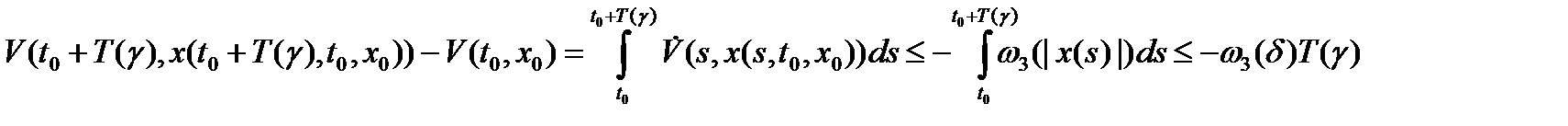Отсюда
. (7)
Если 
, то неравенство (7) невозможно. Значит, найдется 
такое, что 
. Но тогда в силу равномерной устойчивости при всех 
имеем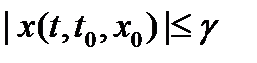 
.■
B классической работе A. M. Ляпунова теорема 3 сформулирована следующим образом: пусть существует определенно-положительная функция 
, допускающая бесконечно малый высший предел, производная которой в силу уравнений (0) определенно отрицательна. Тогда тривиальное решение уравнения (0) асимптотически устойчиво.
Если не предполагать выполненным неравенство (4), то решение 
может не быть асимптотически устойчивым.
Пример 1 (Х. Л. Массера). Определим функцию 
, совпадающую c 
всюду, кроме узких пиков ширины меньше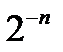 
c центром в точке 
; пусть 
(рис. 5).
Рассмотрим уравнение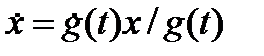 
. Его общее решение имеет вид 
. Отсюда вытекает, что тривиальное решение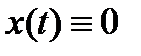 
не является асимптотически устойчивым.
Однако если взять функцию Ляпунова
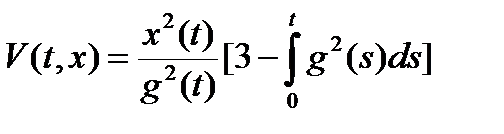, (8)
то получим 
и 
, поскольку 
. Вместе c тем функции (8) не допускает бесконечно малого высшего предела, так как имеются точки 
, где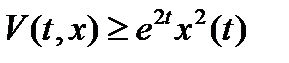 
.
Отметим, что B. П. Марачковым была доказана следующая теорема: пусть правая часть 
уравнения (0) ограничена в 
. Тогда если существует функция 
, удовлетворяющая оценкам (2) и (6), то тривиальное решение уравнения (0) асимптотически устойчиво.
Рисунок 5. Вид функции 
из примера 1.
Теорема 4 (Е. A. Барбашин, П. П. Красовский). Пусть выполнены все условия теоремы 3 и, кроме того,
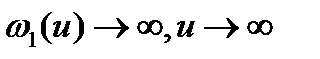. (9)
Тогда решение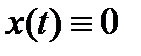 
уравнения (0) асимптотически устойчиво в целом.
□ Возьмем произвольное начальное условие 
и определим такое 
, что 
. B силу (9) такое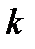 
обязательно найдется. При этом так же, как и в теореме 2, устанавливается, что решение 
не покинет шар 
при 
. Применяя к шару 
теорему 3, получим утверждение теоремы 4.■
При нарушении условия (9) асимптотической устойчивости в целом может не быть.
Рисунок 6. Структура области 
Докажем одну теорему o неустойчивости. Возьмем непрерывно дифференцируемую функцию 
и обозначим через 
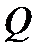область вида 
. Предположим, что область 
обладает следующими свойствами:
) 
состоит из нескольких связных открытых компонент;
) в имеются точки 
c произвольно малой нормой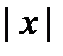 
(рис. 6).
Теорема 5 (теорема Четаева). Пусть существует функция 
такая, что область 
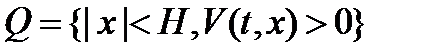удовлетворяет условиям и . Тогда если в области 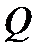функция 
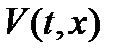ограничена, a ее производная в силу системы (0) определенно-положительна (т. e. 
), то тривиальное решение системы (0) неустойчиво.
□ Согласно условию, в сколь угодно малой окрестности 
начала координат найдется точка 
такая, что 
. На решении 
функция 
не убывает, т. e. 
. Это означает, что через границу 
это решение не может покинуть область 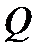. Решение 
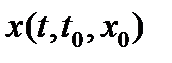не может всегда оставаться в области 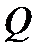. Действительно, в этом случае при 
в силу условия теоремы найдется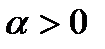 
такое, что 
при 
. Тогда было бы выполнено неравенство
.
Но это невозможно, поскольку 
ограничена в области 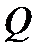. Значит, решение 
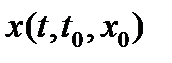обязательно попадет на границу 
области 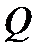за конечное время.■
Замечания. 1. Условия теорем 1-5 можно несколько ослабить. Именно: можно потребовать только, чтобы 
была непрерывной по 
и локально липшицевой по 
. Тогда если в теоремах 1-4 заменить производную в силу системы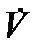 
на правое верхнее производное число в силу системы 
, то утверждения этих теорем останутся справедливыми. В теореме 5 вместо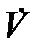 
можно рассматривать правое нижнее производное число 
.
2. Метод функций Ляпунова является универсальным методом исследования устойчивости и большинство теорем метода Ляпунова допускают обращение. Точнее, если функция 
в уравнении (0) непрерывно дифференцируема и начало координат 
устойчиво, то существуют некоторая окрестность 
начала координат и непрерывно дифференцируемая функция 
, определенная на 
, которая удовлетворяет всем условиям теоремы 1. Это утверждение было установлено К. П. Персидским. Обращение теоремы 2 о равномерной устойчивости было установлено Я. Курцвейлем. Х. Л. Macсера доказал теорему, обратную теореме 3 о равномерной асимптотической устойчивости. Обращение теоремы Четаева о неустойчивости получено И. Вркочем.
Устойчивость линейных систем
Устойчивость — свойство САУ возвращаться в заданный или близкий к нему установившийся режим после какого-либо возмущения.
Устойчивая САУ — система, в которой переходные процессы являются затухающими.
Рассмотрим:
— операторная форма записи линеаризированного уравнения.
y(t) = y уст (t)+y п = y вын (t)+y св
y уст (y вын) — частное решение линеаризированного уравнения.
y п (y св) — общее решение линеаризированного уравнения как однородного дифференциального уравнения, то есть
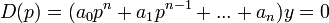
САУ устойчива, если переходные процессы уn(t), вызываемые любыми возмущениями, будут затухающими с течением времени, то есть 
при 
Решая дифференциальное уравнение в общем случае, получим комплексные корни
pi, pi+1 = ±αi ± jβi
Каждой паре комплексно-сопряженных корней соответствует следующая составляющая уравнения переходного процесса:
, где
,
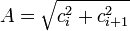Из полученных результатов видно, что:
1. при ∀αi<0,
выполняется условие устойчивости, то есть переходный процесс с течением времени стремится к ууст (теорема Ляпунова 1);
2. при ∃αi>0,
выполняется условие неустойчивости (теорема Ляпунова 2), то есть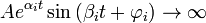 
, что приводит к расходящимся колебаниям;
3. при ∃αi=0 и ∃αi>0,
, что приводит к незатухающим синусоидальным колебаниям системы (система на границе устойчивости) (теорема Ляпунова 3).