Лекция 6а. Расчет надежности с учетом внезапных отказов

В простейшем случае, когда отказы независимы и про­исходят в

случайные моменты времени и среднее значение числа отказов одинаково

для равных по длительности перио­дов работы, надежность устройства

определяется экспонен­циальной формулой

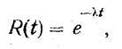
где

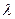— интенсивность отказов;

е — основание натуральных логарифмов (е = 2,7182);

t —время работы, для которого определяется надеж­ность.

Особенностью полученной информации о величине 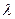яв­ляется весьма большой разброс ее значений. Однако приве­денные в отечественной и зарубежной литературе данные можно использовать для ориентировочных расчетов (см. табл. 3).

Вычисленное R(t) представляет собой вероятность того, что устройство с интенсивностью отказов 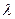не откажет в те­чение времени t. Эта формула справедлива для всех устройств, которые прошли приработку и не испытывают пока влияния износа и старения. Период работы, для

кото­рого справедливо выражение, называется нормальной экс­плуатацией устройства.

Длительность этого периода для различных устройств различна, однако время в формуле никогда не может быть больше периода нормальной эксплуатации устройства. В пе­риод нормальной эксплуатации надежность устройства при­мерно одинакова для равных по длительности периодов ра­боты, но с увеличением общего времени работы надежность снижается.

Например, R(t) для элемента с 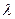= 0,0001 l/ч для отрезка времени 10 ч, выбранного в любом месте периода нормальной эксплуатации устройства, составит

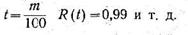
Вероятность же того, что устройство не откажет за период работы, равный 1000 ч

Параметр 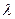в этом случае полностью определяет надежность устройства.

При предварительной оценке надежности устройства удоб­но пользоваться обратной величиной, называемой средней наработкой на отказ m, которая равна

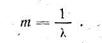
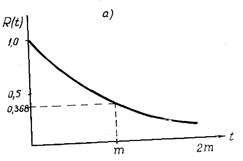
На рис. 3, а приведен график R(t). Отметим, что абсцис­са t не измеряет общего времени работы устройства. Она отражает только часы

произвольно выбранного периода ра­боты, начало которого в частном

случае может совпадать и с началом работы устройства в эксплуатации.

При определении надежности устройства обычно требуется найти

вероятность безотказной работы в течение интересую­щего отрезка времени, длительность которого всегда много меньше средней наработки на отказ. Следовательно, расчет надежности производится для промежутков времени, которые соответствуют крайней левой части кривой надежности (см. рис. 3, а). На кривой, представленной на рис. 3, б, имеется ряд точек, которые легко запомнить и с помощью которых можно производить первое грубое предсказание надежности устройства. Так, вероятность безотказной работы устройства в течение интервала времени t—m равна 0,368 (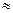 0,37).

Для

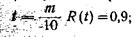
ДЛЯ

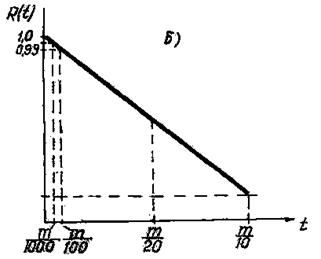Рис. 12

Эти точки на кривой надежности применимы к любым элементам и системам при учете только внезапных отказов с частотой 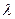. Следовательно, зависимость R(t), в которой m используется как единица времени, является универсальной кривой надежности.

Система, состоящая из п одинаковых элементов, у каж­дого из которых средняя наработка на отказ m_i, будет иметь среднюю наработку на отказ если отказ любого из этих элементов вызывает отказ системы (последовательное соеди­нение). Это замечание также относится и к неоднотипным элементам, если под m_i понимать среднее значение нарабо­ток на отказ неоднотипных элементов.

Для оценки надежности сложной системы (локомотив или его узлы) в первую очередь необходимо установить, каким образом отдельные узлы влияют на безотказность системы в целом. Обычно считают, что система отказывает при отказе хотя бы одного входящего в нее элемента и отказы отдель­ных элементов независимы. В этом случае R (t) нерезервиро­ванной системы с учетом только внезапных отказов при усло­вии, что все элементы работают одновременно, может быть определено по выражению

где

п — число элементов, составляющих систему;

Ri (t) — надежность i-го элемента.

Таким образом, надежность любой системы определяется произведением R (t) входящих в нее элементов.

Для оценки надежности системы в целом без разбивки ее на звенья или смысловые блоки можно использовать вели­чину суммарной интенсивности отказов системы ^, равную сумме интенсивностей отказов элементов, входящих в эту си­стему:

Обычно локомотивная система объединяет несколько групп аналогичных элементов. Для любых элементов интенсивность отказов, а следовательно, и надежность зависит от режимов работы и времени.

На первом этапе расчета, при определении надежности только с учетом внезапных отказов, когда еще не известны режимы работы, можно предположить, что все элементы системы работают в номинальном режиме, т. е. интенсивность отказов у них постоянна и равна табличным значениям. В табл. 3 приведены значения 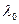о и 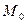для наиболее часто встречающихся элементов.

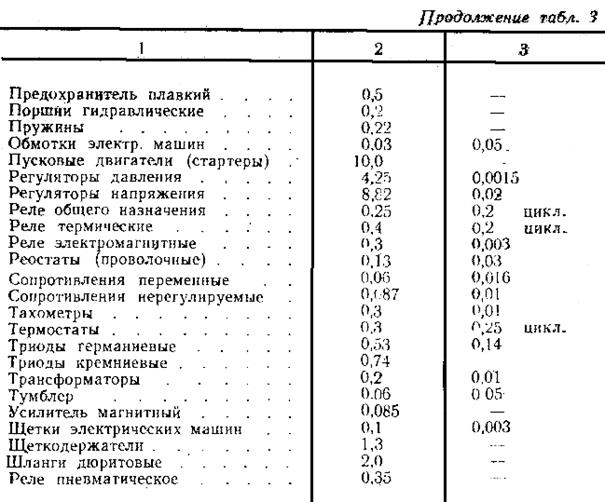
Примечание. 1. При умножении данных гр. 2 на 10 ^-6 — размер­ность 1/ч, при умножении данных гр. 3 на 10⁶, если нет наименования, размерность в часах. 2. Данные таблицы могут быть использованы только для учебных либо сравнительных расчетов надежности. Более полные таблицы см. [2, 4, 5].