Лекция 8.
(с.)
Общие теоремы об устойчивости не позволяют даже в простейших случаях по коэффициентам уравнения без вычислений судить об устойчивости его решений. Получение таких коэффициентных условий даже для частных классов уравнений представляет большой интерес. В первую очередь изучаются линейные уравнения c постоянными коэффициентами.
1. Критерий Рауса - Гурвица. Рассмотрим систему линейных дифференциальных уравнений c постоянными коэффициентами
 (1)
(1)
Напомним некоторые сведения, касающиеся структуры общего решения уравнения (1).
Предположим сначала, что матрица  имеет только простые, собственные значения
имеет только простые, собственные значения  и собственные векторы
и собственные векторы  , т. e.
, т. e.
Рис. 1. Жорданова форма матрицы 
 . Тогда общее решение уравнения (1) имеет вид
. Тогда общее решение уравнения (1) имеет вид
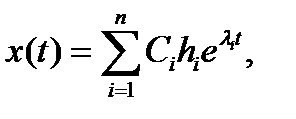
где  - произвольные постоянные.
- произвольные постоянные.
При наличии кратных собственных значений для построения общего решения уравнения (1) приведем сначала матрицу  к жордановой форме. Жордановой формой матрицы называется клеточно-диагональная форма, в которой главную диагональ образуют клетки Жордана, a все остальные элементы равны нулю.
к жордановой форме. Жордановой формой матрицы называется клеточно-диагональная форма, в которой главную диагональ образуют клетки Жордана, a все остальные элементы равны нулю.
При этом клеткой Жордана называется квадратная матрица, y которой на главной диагонали находится одно и то же число, элементы одного ряда выше главной диагонали равны единице, a все прочие элементы нулю (см. рис. 1, где изображены клетки Жордана, a все элементы вне диагональных блоков равны нулю).Возможны различные способы приведения матрицы квадратной матрицы  размерности
размерности  к жордановой форме. Приведем один из них, состоящий из следующих этапов:
к жордановой форме. Приведем один из них, состоящий из следующих этапов:
10. Для каждого  находят наибольший общий делитель
находят наибольший общий делитель  всех миноров порядка
всех миноров порядка  характеристической матрицы
характеристической матрицы  . Старшие коэффициенты y всех полиномов
. Старшие коэффициенты y всех полиномов  берут равными единице. При этом
берут равными единице. При этом
 .
.
20. Находят инвариантные многочлены  (называемые так же инвариантными множителями) по формулам
(называемые так же инвариантными множителями) по формулам
 .
.
30. Каждый инвариантный многочлен раскладывают на различные неприводимые многочлены, называемые элементарными делителями характеристической матрицы 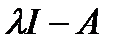 или просто матрицы
или просто матрицы  . Элементарный делитель представляют в виде степени одной из разностей
. Элементарный делитель представляют в виде степени одной из разностей  , где
, где  — собственные значения матрицы
— собственные значения матрицы  . Таким образом,
. Таким образом,  имеет вид
имеет вид
 .
.
Отметим, что произведение всех элементарных делителей равно произведению всех инвариантных множителей и равно  .
.
40. Каждому элементарному делителю  сопоставляют клетку Жордана порядка
сопоставляют клетку Жордана порядка  с числом
с числом  на главной диагонали. Клеточно-диагональная матрица, y которой на главной диагонали находятся все построенные указанным образом клетки Жордана, и есть жорданова форма матрицы
на главной диагонали. Клеточно-диагональная матрица, y которой на главной диагонали находятся все построенные указанным образом клетки Жордана, и есть жорданова форма матрицы  . Жорданова форма матрицы единственна с точностью до порядка расположения ее клеток Жордана на главной диагонали.
. Жорданова форма матрицы единственна с точностью до порядка расположения ее клеток Жордана на главной диагонали.
Приведем теперь формулы, определяющие общее решение уравнения (1) в случае кратных корней. Пусть  ‑
‑  -кратное собственное значение матрицы
-кратное собственное значение матрицы  . Ему соответствует некоторое количество собственных векторов. Степень вырождения собственного значения
. Ему соответствует некоторое количество собственных векторов. Степень вырождения собственного значения  равна максимальному числу
равна максимальному числу  линейно независимых собственных векторов, отвечающих
линейно независимых собственных векторов, отвечающих  . Число
. Число  равно также числу клеток Жордaна, соответствующих
равно также числу клеток Жордaна, соответствующих  . Обозначим через
. Обозначим через  одну из этих клеток. Если размерность клетки Жордана
одну из этих клеток. Если размерность клетки Жордана  есть
есть  , то
, то
 .
.
Отсюда, в частности, видно, что жорданова форма матрицы  является диагональной, если кратность любого ее собственного значения равна его степени вырождения. B этом случае все собственные значения имеют простые элементарные делители. Каждой клетке Жордaна
является диагональной, если кратность любого ее собственного значения равна его степени вырождения. B этом случае все собственные значения имеют простые элементарные делители. Каждой клетке Жордaна  соответствует серия векторов
соответствует серия векторов  (своих для каждой клетки), таких, что
(своих для каждой клетки), таких, что
 .
.
Векторы  , где
, где 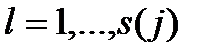 , каждой серии линейно независимы между собой. Подпространство, натянутое на все векторы
, каждой серии линейно независимы между собой. Подпространство, натянутое на все векторы 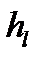 , соответствующие клетке
, соответствующие клетке  , является инвариантным, циклическим и имеет размерность, равную размерности серии, т. е: равную
, является инвариантным, циклическим и имеет размерность, равную размерности серии, т. е: равную  . В базисе, составленном из векторов всех серий, матрица
. В базисе, составленном из векторов всех серий, матрица  имеет жорданову форму.
имеет жорданову форму.
Вернемся к уравнению (1). Решениями этого уравнения являются функции вида
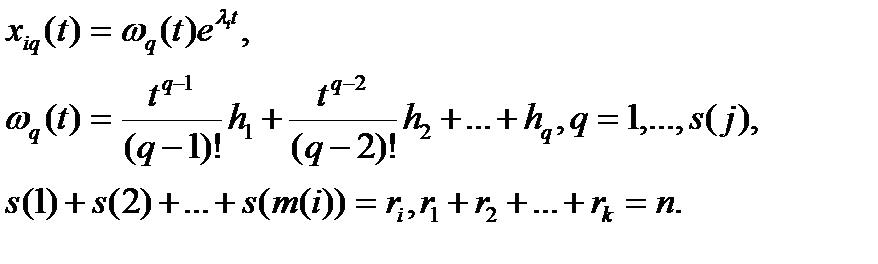 (2)
(2)
Количество линейно независимых решений вида (2) равно  . Общее решение уравнения (1) есть линейная комбинация из частных решений вида (2).
. Общее решение уравнения (1) есть линейная комбинация из частных решений вида (2).
Из описанного представления общего решения линейной стационарной системы немедленно вытекает следующая теорема.
Теорема 1. Для устойчивости тривиального решения уравнения (1) необходимо и достаточно, чтобы все собственные значения  матрицы
матрицы  удовлетворяли условию
удовлетворяли условию 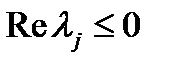 , причем собственные значения
, причем собственные значения  такие, что
такие, что  , имеют простые элементарные делители (т. e. в формуле (2) все
, имеют простые элементарные делители (т. e. в формуле (2) все  ). Для асимптотической устойчивости уравнения (1) необходимо и достаточно, чтобы
). Для асимптотической устойчивости уравнения (1) необходимо и достаточно, чтобы 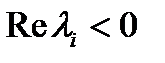 .
.
Таким образом, устойчивость асимптотическая устойчивость или неустойчивость уравнения (1) определяется расположением относительно мнимой оси корней характеристического уравнения матрицы  :
:
 . (3)
. (3)
Здесь 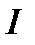 — единичная (
— единичная ( )-матрица. Раскрывая определитель, можно привести уравнение (3) к виду
)-матрица. Раскрывая определитель, можно привести уравнение (3) к виду
 . (4)
. (4)
Будем говорить, что многочлен  является устойчивым многочленом (многочленом Гурвица), если все его корни
является устойчивым многочленом (многочленом Гурвица), если все его корни  имеют отрицательную вещественную часть, т. e.
имеют отрицательную вещественную часть, т. e.
 . (5)
. (5)
При выполнении условия (5) матрицу  также называют устойчивой.
также называют устойчивой.
Теорема 2 (А. Стодола). Все коэффициенты устойчивого многочлена положительны.
□ Пусть  — корни устойчивого многочлена
— корни устойчивого многочлена 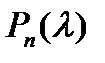 . Тогда
. Тогда  и, раскладывая
и, раскладывая  на множители, имеем
на множители, имеем
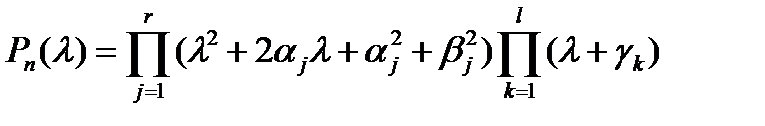 .
.
Таким образом,  представлен в виде произведения многочленов c положительными коэффициентами. Поэтому все его коэффициенты
представлен в виде произведения многочленов c положительными коэффициентами. Поэтому все его коэффициенты  . ■
. ■
Положительность коэффициентов есть необходимое, но не достаточное условие для выполнения неравенств (5). Например, многочлен  имеет корни
имеет корни  .
.
Сформулируем теперь необходимый и достаточный признак устойчивости. Матрицей Гурвица  многочлена (4) называется матрица вида
многочлена (4) называется матрица вида
 . (6)
. (6)
В матрице (6) все 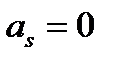 при
при  и
и  . Например, для многочлена шестой степени матрица Гурвица такова:
. Например, для многочлена шестой степени матрица Гурвица такова:
 (7)
(7)
Критерий Paуса — Гурвица. Для того чтобы многочлен  c
c  и
и 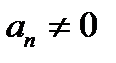 был устойчивым, необходимо и достаточно, чтобы были положительны все главные диагональные миноры
был устойчивым, необходимо и достаточно, чтобы были положительны все главные диагональные миноры

его матрицы Гурвица  .
.
Критерий Льенара ‑ Шипара. Для того чтобы многочлен c положительными коэффициентами был устойчивым, необходимо и достаточно выполнение одного из двух условий: а)  , б)
, б) 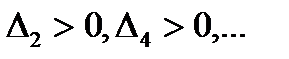 .
.
В качестве примера рассмотрим многочлен
 .
.
Из вида матрицы (6), используя критерий Льенара ‑ Шипара, получим, что многочлен 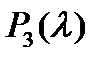 является устойчивым, если
является устойчивым, если 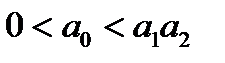 .
.
2. Частотные критерии устойчивости. Применение критерия Рауса - Гурвица к реальным системам автоматического регулирования приводит к сложным вычислениям и не позволяет выявить влияние отдельных параметров на устойчивость системы. Более удобными в приложениях оказываются частотные критерии A. B. Михайлова и Г. Найквиста.
Рассмотрим многочлен (4). Положим  и построим годограф Михайлова (амплитудно-фазовую характеристику)
и построим годограф Михайлова (амплитудно-фазовую характеристику)  этого многочлена:
этого многочлена:
 .
.
Геометрически  есть вектор в комплексной плоскости
есть вектор в комплексной плоскости  , началом которого служит точка
, началом которого служит точка  — корень многочлена
— корень многочлена  , a концом - точка
, a концом - точка  .
.
Так как 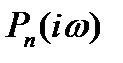 — комплексное число, то
— комплексное число, то
 . (8)
. (8)
Если корень 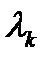 лежит в левой полуплоскости
лежит в левой полуплоскости  , то при изменении
, то при изменении 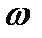 от
от  до
до  вектор
вектор  вращается в положительном направлении (против хода часовой стрелки) и приращение аргумента равно
вращается в положительном направлении (против хода часовой стрелки) и приращение аргумента равно  :
:
 . (9)
. (9)
Если же корень  лежит в правой полуплоскости, то вектор (
лежит в правой полуплоскости, то вектор ( ) вращается по ходу часовой стрелки и
) вращается по ходу часовой стрелки и
 .
.
Из соотношений (8) и (9) вытекает следующая теорема.
Теорема 3. Многочлен  , не имеющий чисто мнимых корней, является устойчивым тогда и только тогда, когда
, не имеющий чисто мнимых корней, является устойчивым тогда и только тогда, когда
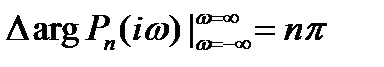 (10)
(10)
Для упрощения условия (10) отделим действительную и мнимую части  . Имеем
. Имеем
 .
.
Отсюда видно, что  есть четная функция от
есть четная функция от  , a
, a  - нечетная. Поэтому годограф многочлена
- нечетная. Поэтому годограф многочлена  состоит из двух частей, симметричных относительно действительной оси, первая из которых соответствует изменению
состоит из двух частей, симметричных относительно действительной оси, первая из которых соответствует изменению  от
от  до 0, a вторая — от 0 до
до 0, a вторая — от 0 до  . В результате получаем следующее утверждение.
. В результате получаем следующее утверждение.
Критерий Михайлова. Для устойчивости многочлена  , не имеющего чисто мнимых корней, необходимо и достаточно, чтобы
, не имеющего чисто мнимых корней, необходимо и достаточно, чтобы
 . (11)
. (11)
На рис. 2 приведены различные годографы Михайлова для 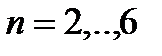 . Чем ближе годограф подходит к началу координат, тем меньше запас устойчивости. Если годограф проходит через начало координат, то система находится на границе области устойчивости. Таким образом, критические значения параметров
. Чем ближе годограф подходит к началу координат, тем меньше запас устойчивости. Если годограф проходит через начало координат, то система находится на границе области устойчивости. Таким образом, критические значения параметров 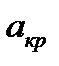 и частоты
и частоты  , линейной стационарной системы c характеристическим. уравнением (4) находят из условий
, линейной стационарной системы c характеристическим. уравнением (4) находят из условий

Чтобы подчеркнуть зависимость многочлена (4) от параметров  , он обозначен через
, он обозначен через  . Интересно отметить, что на практике амплитудно-фазовую характеристику можно определить экспериментально, подавая на вход линейной стационарной системы сигнал частоты
. Интересно отметить, что на практике амплитудно-фазовую характеристику можно определить экспериментально, подавая на вход линейной стационарной системы сигнал частоты  и амплитуды 1. На выходе системы получится сигнал той же частоты
и амплитуды 1. На выходе системы получится сигнал той же частоты  , a амплитуда
, a амплитуда  окажется сдвинутой по фазе на
окажется сдвинутой по фазе на  относительно входного сигнала.
относительно входного сигнала.
3. Система автоматической подстройки частоты гетеродинного приемника. B гетеродинных приемниках для обеспечения качественного звучания основное усиление производится на фиксированной, так называемой промежуточной частоте  Поскольку частота принимаемого сигнала
Поскольку частота принимаемого сигнала  постоянно меняется из-за разного рода неконтролируемых возмущений, для обеспечения хорошей работы гетеродинного приемника в его состав вводят систему автоматической подстройки частоты (АПЧ). Задачей системы АПЧ является поддержание заданного значения
постоянно меняется из-за разного рода неконтролируемых возмущений, для обеспечения хорошей работы гетеродинного приемника в его состав вводят систему автоматической подстройки частоты (АПЧ). Задачей системы АПЧ является поддержание заданного значения  . Одна из возможных систем АПЧ изображена на рис. 3.
. Одна из возможных систем АПЧ изображена на рис. 3.
Рис. 2. Годографы Михайлова для устойчивых систем при n=2,3,4,5,6
Рис. 3. Система автоматической подстройки частоты гетеродинного приемника: 1 — смеситель; 2 — усилитель промежуточной частоты; 3— дискриминатор; 4— усилитель; 5 – управляющий элемент гетеродина
Работа каждого из устройств 1-5 описывается следующими соотношениями, записанными сразу для отклонений частот  :
:
1. Смеситель:  .
.
2. Усилитель промежуточной 'частоты (УПЧ):

3. Дискриминатор:  ,
,
4. Усилитель:  .
.
5. Управляющий элемент гетеродина:
 .
.
Входной величиной.АПЧ будем считать  , а выходом
, а выходом 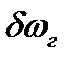 , т, e, будем рассматривать АПЧ как следящую систему. Применяя операторный метод, получим:
, т, e, будем рассматривать АПЧ как следящую систему. Применяя операторный метод, получим:

Окончательно получим уравнение АПЧ в виде
 (12)
(12)
Установим условия устойчивости АПЧ, описываемой уравнением (12), Воспользуемся критерием Михайлова, Построим годограф:
 .
.
Отделим действительную и мнимую части:
 .
.
Определим критический коэффициент усиления  и, критическую частоту
и, критическую частоту  из условий
из условий  . Из условия
. Из условия  находим, что
находим, что

a из условии  — что
— что

При значениях  получим
получим  . Следовательно, такая система АПЧ при
. Следовательно, такая система АПЧ при  устойчива, a при
устойчива, a при  - неустойчива.
- неустойчива.
4. Линейные одноконтурные системы автоматического регулирования. Вывод, аналогичный предыдущему, верен и для любой одноконтурной системы автоматического регулирования (САР), содержащей произвольное число звеньев (рис. 4). Пусть характеристическое уравнение одноконтурной системы имеет вид
 (13)
(13)
Первые  сомножителей в (13) соответствуют апериодическим звеньям, вторые
сомножителей в (13) соответствуют апериодическим звеньям, вторые  — колебательным.
— колебательным.
Рис. 4. Произвольная одноконтурная система автоматического регулирования
Теореме 4. Для любой одноконтурной САР c характеристической функцией (13) существует критическое значение коэффициента усиления  такое, что при
такое, что при  система устойчива, a при
система устойчива, a при  она неустойчива.
она неустойчива.
5. Робастная устойчивость. Приведенные в теоремах этого параграфа условия устойчивости получены в предположении, что все коэффициенты системы  , т. e. все элементы постоянной матрицы
, т. e. все элементы постоянной матрицы  , априори известны точно. Однако указанное предположение не всегда выполняется. В реальной ситуации зачастую бывает известна лишь некоторая область
, априори известны точно. Однако указанное предположение не всегда выполняется. В реальной ситуации зачастую бывает известна лишь некоторая область  , которой принадлежит матрица
, которой принадлежит матрица  . Ясно, что если устойчивость имеет место при любой матрице
. Ясно, что если устойчивость имеет место при любой матрице  из области
из области 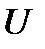 , то реальная система также будет устойчива. Оказывается, что в некоторых ситуациях об устойчивости всех систем при произвольных матрицах
, то реальная система также будет устойчива. Оказывается, что в некоторых ситуациях об устойчивости всех систем при произвольных матрицах  можно судить по их отдельным представителям.
можно судить по их отдельным представителям.
Приведем соответствующие утверждения.
Пусть  — характеристический. многочлен матрицы
— характеристический. многочлен матрицы  , a
, a  - множество всех таких многочленов, соответствующих всем матрицам
- множество всех таких многочленов, соответствующих всем матрицам  . Произвольный многочлен
. Произвольный многочлен  запишем в виде
запишем в виде
 (14)
(14)
Предположим, что известны границы изменения коэффициентов  , когда многочлен
, когда многочлен  пробегает множество
пробегает множество  . Иначе говоря, предположим, что известны числа
. Иначе говоря, предположим, что известны числа  такие, что
такие, что
 (15)
(15)
Оказывается, что для проверки устойчивости всего бесконечного множества многочленов  достаточно убедиться в устойчивости только четырех многочленов:
достаточно убедиться в устойчивости только четырех многочленов:  .
.
Коэффициенты  многочлена
многочлена  таковы:
таковы:
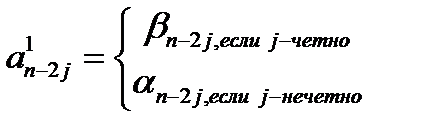

Коэффициенты 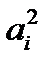 многочлена
многочлена  имеют вид:
имеют вид:
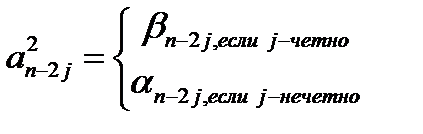
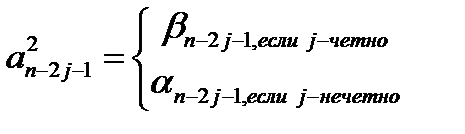
Коэффициенты  многочлена
многочлена  имеют вид:
имеют вид:


Коэффициенты  многочлена
многочлена  таковы:
таковы:


Теорема 5 (B. Л. Харитонов). Для того чтобы любой многочлен  вида (14) с коэффициентами; удовлетворяющими условиям (15), был устойчивым, необходимо и достаточно, чтобы все четыре многочлена
вида (14) с коэффициентами; удовлетворяющими условиям (15), был устойчивым, необходимо и достаточно, чтобы все четыре многочлена  были устойчивыми.
были устойчивыми.
Пример 1. Установим необходимые и достаточные условия асимптотической устойчивости множества скалярных систем третьего порядка
 (16)
(16)
с коэффициентами, удовлетворяющими условиям
 (17)
(17)
Характеристический многочлен уравнения (16) имеет вид

Построим многочлены 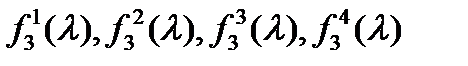 :
:
 (18)
(18)
Запишем условия устойчивости многочленов (18). Они имеют вид
 (19)
(19)
Поскольку  и
и  меньше любого из произведений
меньше любого из произведений  ,
,  и
и 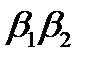 , все условия (19) будут выполняться одновременно, если окажется выполненным лишь одно неравенство
, все условия (19) будут выполняться одновременно, если окажется выполненным лишь одно неравенство
 (20)
(20)
Таким образом, все уравнения из множества (16) с коэффициентами, удовлетворяющими условию (17), устойчивы, если выполнены неравенства (20). Эти неравенства представляются весьма естественными. Если же они нарушаются, то, взяв уравнение (16), у которого  , получим неустойчивое уравнение.
, получим неустойчивое уравнение.