ЛАБОРАТОРНАЯ РАБОТА №8
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫЛИНЗЫИ ДЛИНЫСВЕТОВОЙ ВОЛНЫС ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА И ОПТИЧЕСКОГО СФЕРОМЕТРА
Цель работы: ознакомление с явлением интерференции света в тонких прозрачных изотропных средах.
Приборы и принадлежности: микроскоп с осветителем и набором светофильтров, плоскопараллельная пластинка с линзой в оправе, сферометр ИЗС-7.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
Если тонкую плёнку осветить монохроматическим светом, то вследствие разделения световой волны на две при отражении и преломлении света на передней и задней поверхностях плёнки возникают две когерентные волны. При сложении двух когерентных волн образуется интерференционная картина, состоящая из чередующихся максимумов и минимумов освещенности. Результат интерференции зависит от оптической разности хода (D), полученной при интерференции двух когерентных волн, идущих в одном направлении.
При наблюдении интерференции в отраженном свете оптическая разность хода равна

где n – показатель преломления плёнки, h – толщина пленки, r – угол преломления,  l/2 – дополнительная разность хода, возникающая из-за изменения фазы на противоположную при отражении от плёнки.
l/2 – дополнительная разность хода, возникающая из-за изменения фазы на противоположную при отражении от плёнки.
Прозрачная пленка может иметь вид клина. Интерференционная картина, получается при отражении света от клина, носит название «полос равной толщины», которые локализованы на поверхности клина.
В работе для получения интерференционной картины используется воздушный клин, образованный между плоскопараллельной пластиной C и плосковыпуклой линзой l (рис. 9.1).
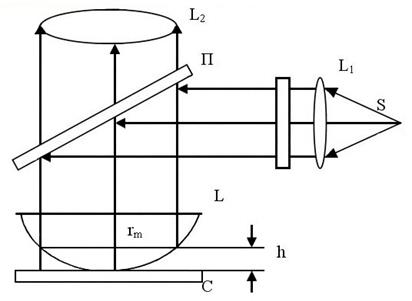
Рис. 9.1.
Интерференционная картина получила название «колец Ньютона». Она состоит из чередующихся светлых и тёмных колец с темным центральным пятном. Для воздушного клина в случае нормального падения монохроматического света разность волн равна
D=2h +(l/2);
условия максимума и минимума интенсивности света определяются соответственно выражениями
D=2m (l/2) и D=2(m +1)(l/2).
Используя приведенные условия, можно получить выражение для радиусов n -го и m -го темных колец Ньютона:
rn =  ; r m =
; r m =  .
.
Тогда радиус кривизны линзы R равен:
 .
.
Эта формула может служить как для определения радиуса кривизны линзы R, так и для определения длины волны света l.
ОПИСАНИЕ УСТАНОВКИ
Для наблюдения колец Ньютона в работе используется установка, основной частью которой является плосковыпуклая линза с большим радиусом кривизны, положенная на плоскопараллельную пластинку. Интерференционная картина в отраженном свете в виде колец Ньютона наблюдается с помощью микроскопа. Радиус кривизны линзы определяют сферометром ИЗС-7 (рис. 9.2).

Рис. 9.2.
Внутри корпуса 1 сферометра расположен измерительный стержень с миллиметровой шкалой, обеспечивающий контакт сферического наконечника с измеряемым изделием 2. В верхней части корпуса помещается измерительное кольцо 3 с укрепленными на нем тремя шариками. Упор 4 служит для прижатия изделия к измерительному кольцу. Для установки начального отсчета на ноль или на требуемую величину по миллиметровой шкале измерительного микроскопа служит винт 5. Для отвода измерительного стержня вниз служит рычаг-арретир 6. Маховичок 7 окулярного микрометра служит для установки вертикального индекса на нулевое деление круговой шкалы. В установке используется трансформатор 8.
ВЫПОЛНЕНИЕ РАБОТЫ
УПРАЖНЕНИЕ I
Определение радиуса кривизны линзы с помощью
«колец Ньютона» и сферометра
1. Под объектив микроскопа поместить пластинку с линзой в оправе, включить осветитель и, перемещая тубус микроскопа и линзу, сфокусировать микроскоп на четкое видение интерференционной картины («кольца Ньютона»).
2. Используя светофильтр (l=530 нм), провести измерения диаметров темных колец во взаимно перпендикулярных направления dx и dy, начиная с колец более высоких порядков. Цена деления окулярного микрометра 0,02 мм. Найти среднее значение d.
3. Вычислить радиус кривизны линзы по формуле:
 , (9.1)
, (9.1)
где dm и dn – диаметры m -го и n -го темных колец, наиболее удаленных друг от друга.
4. Определить радиус кривизны линзы с помощью сферометра ИЗС-7. Определение радиуса кривизны линзы на сферометре сводится к измерению стрелки АD или АК шарового сегмента и вычислению радиуса кривизны (рис. 9.3). Измерение стрелки отдельной сферической поверхности производится следующим образом.
С помощью рычага-арретира измерительный стержень отводят вниз, и на измерительное кольцо осторожно накладывают плоскую стеклянную пластинку.



Рис. 9.3. Рис. 9.4.
Рычаг отпускают, и измерительный стержень, плавно поднимаясь, приходит в соприкосновение с пластинкой. Затем с помощью микроскопа производят начальный отсчет по шкале. Для повышения точности измерения отсчеты повторяют 3-5 раз и вычисляют среднее. Далее на кольцо осторожно кладут измеряемую линзу со сферической поверхностью и аналогичным образом производят 3-5 измерений, затем вычисляют среднее. Разность двух средних отсчётов по шкале и даст величину стрелки АК и АD измеряемой сферической поверхности.
Отсчет с помощью микроскопа со
спиральным микрометром
В поле зрения отчетного микроскопа (рис. 9.4) одновременно видны: 2-3 штриха миллиметровой шкалы, обозначенные крупными цифрами «11», «12», «13», неподвижная шкала десятых долей миллиметра с делениями от «0» до «10», круговая шкала для отсчёта сотых и тысячных долей миллиметра и двойные витки спирали. Чтобы произвести отсчет, необходимо предварительно маховиком 7 подвести двойной виток спирали так, чтобы миллиметровый штрих в зоне двойных витков оказался точно посредине между линиями витка. Индексом для отсчета миллиметров служит нулевой штрих десятых долей миллиметра.
На рис. 9.4 миллиметровый штрих «12» прошел нулевой штрих шкалы десятых долей миллиметра, а ближайший штрих «13» еще не дошел до нулевого штриха шкалы десятых долей миллиметра. Отсчет будет 12 мм плюс отрезок штриха «12» до нулевого штриха шкалы десятых долей. В нашем случае число десятых долей миллиметра обозначено цифрой "2" последнего пройденного штриха шкалы десятых долей. Сотые и тысячные доли миллиметра отсчитываются по круговой шкале, указателем для отсчета по ней служит стрелка; цена деления круговой шкалы — 0,001 мм. На рисунке 72-й штрих прошел указатель и часть интервала шкалы. Эту часть интервала определяют на глаз, она примерно равна 0,5 делений круговой шкалы. Окончательный отсчет будет 12,2725. Вычисление радиуса кривизны для изделий с выпуклой поверхностью производится по следующей формуле:
 ,
,
где r – радиус измерительного кольца (выбрано кольцо r =15,007 мм),
r – радиус шарика кольца (r=2,355 мм), h – измерительная стрелка шарового сегмента измеряемой сферической поверхности.
Найденный радиус кривизны необходимо сравнить с расчетным, полученным по формуле (9.1).
УПРАЖНЕНИЕ II