При нахождении угла между прямой/вектором и плоскостью удобно применять векторное произведение, чтобы найти нормаль к плоскости, если не дано уравнение плоскости.
Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор  , длина которого численно равна площади параллелограмма построенного на векторах
, длина которого численно равна площади параллелограмма построенного на векторах 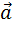 и
и  , перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от
, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от 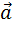 к
к  вокруг вектора
вокруг вектора  осуществлялось против часовой стрелки, если смотреть с конца вектора
осуществлялось против часовой стрелки, если смотреть с конца вектора  .
.
Векторное произведение двух векторов можно найти при помощи матрицы размером  .
.
Даны векторы  и
и  ,лежащие в плоскости α, тогда
,лежащие в плоскости α, тогда

Другими словами, произведение векторов равно

Коэффициенты при i, j, k и будут являться искомыми координатами нормали к плоскости α.
Пример: Найти координаты нормали к плоскости, если координаты векторов, принадлежащих этой плоскости равны
 = {1; 2; 3} и
= {1; 2; 3} и  = {2; 1; -2}.
= {2; 1; -2}.
Решение:

Координаты вектора, перпендикулярного к данной плоскости, будут равны 
 {-7; 8; -3}
{-7; 8; -3}
Уравнение плоскости, проходящей через три точки
|



|

 Пусть в пространстве заданы точки не лежащие на одной прямой М1, М2, М3, заданные точки определяют единственную плоскость. Составим ее уравнение.
Пусть в пространстве заданы точки не лежащие на одной прямой М1, М2, М3, заданные точки определяют единственную плоскость. Составим ее уравнение.

|
|

 Для это выберем на плоскости произвольную т.М, которая имеет не фиксированные, а переменные координаты (обычно обознч. x,y,z).
Для это выберем на плоскости произвольную т.М, которая имеет не фиксированные, а переменные координаты (обычно обознч. x,y,z).
Составим вектора:


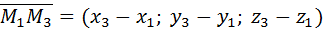
Т.к. все три точки лежат в одной плоскости => все вектора лежат в одной плоскости, такие вектора называют компланарными.
Это значит, что смешанное векторное произведение равно нулю.
 = 0
= 0
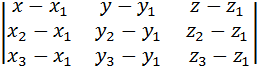 = 0 - уравнение плоскости, проходящей через три точки
= 0 - уравнение плоскости, проходящей через три точки
Примеры решения задач с разбором:
1. В правильной шестиугольной призме A...F1,все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BD1
Решение:

1) Определим координаты нужных точек:




2) Получим необходимые векторы для решения задачи и вычислим их координаты:

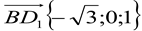
3)

Ответ: 0,8
2. В единичном кубе A..D1 найдите косинус угла между AE и BF, где Е – середина ребра A1D1, а F – середина ребра B1C1
Решение:

1) Найдем необходимые точки для решения задачи:
A (1;0;0) B(1;1;0)
E (1;  ;1) F(
;1) F( ;1;1)
;1;1)
2) Найдем координаты необходимых векторов:

3) Через скалярное произведение вычислим косинус:

Ответ: 0,8
3. В правильной треугольной призме ABCA1B1C1 все ребра которой равны 1, найдите косинус угла между прямыми AD и CE, где D и E - соответственно середины ребер A1C1 и B1C1
Решение:

1) Найдем координаты необходимых для решения задачи точек:
C(0;0;0) E( ) A(1;0;0) D(
) A(1;0;0) D( )
)
2) Вычислим координаты направляющих векторов прямых AD и CE:
 |  | ||
3) Вычислим косинус угла между векторами:
 | |||
 | |||
4. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки Е и F – середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF.

 Решение:
Решение:
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 |
Ответ:
5. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите угол между прямой DE, где Е - середина апофемы SF грани ASB, и плоскостью ASC
Решение:

1) Для того, чтобы найти угол между плоскостью и прямой, нужно выделить вектор нормали плоскости и направляющий вектор данной прямой. Из обозначенных точек найдем координаты вектора нормали плоскости (CAS) 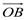 и направляющий вектор прямой
и направляющий вектор прямой  :
:

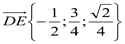
2) Найдем угол между этими векторами:



6. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найти косинус угла между прямыми BA1 и  .
.
 Решение:
Решение:
1.Вводим систему координат xyz с началом в т.E.
2.а) Найдем координаты направляющего вектора прямой A1B, для этого найдем координаты точек A1 и B.
 Длину отрезка AE найдем по теореме косинусов из треугольника AOE:
Длину отрезка AE найдем по теореме косинусов из треугольника AOE:



 Чтобы найти координаты вектора, из координат конца вычтем координаты начала. Получим:
Чтобы найти координаты вектора, из координат конца вычтем координаты начала. Получим:
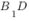




 б) Найдем координаты направляющего вектора прямой, для этого найдем координаты точек и
б) Найдем координаты направляющего вектора прямой, для этого найдем координаты точек и
 | |||
 | |||
 3.Найдем косинус угла между векторами и.
3.Найдем косинус угла между векторами и.


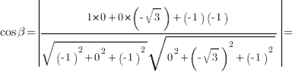
Ответ:
 7. В единичной призме
7. В единичной призме  точка М лежит на
точка М лежит на  , при этом AM:M
, при этом AM:M  как 1:3. Найдите угол между CM и AM.
как 1:3. Найдите угол между CM и AM.
1. Вводим декартову систему координат xyz с началом отсчёта в т.B.
2. Находим координаты точек C,M,A.
a) Угол между осью х и CB равен 90-60=30o
 Отсюда, расстояние от т.С (CK) до оси х равно ½ (катет, лежащий напротив угла в 300)
Отсюда, расстояние от т.С (CK) до оси х равно ½ (катет, лежащий напротив угла в 300)
б) По теореме Пифагора: 
в) 
3. Находим координаты векторов 

|

3. Находим косинус угла между 
4. 
5. По таблице Брадиса находим искомый угол.
Ө=47o
Ответ: Ө=47о

 8. Точки
8. Точки  — середины ребер и соответственно куба
— середины ребер и соответственно куба  Найти угол между прямой
Найти угол между прямой  и плоскостью, проходящей через точку
и плоскостью, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой 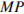 .
.

Решение:
Координатно-векторный способ.
Пусть ребро куба равно 2.
Введем декартову систему координат, как показано на рис.
Найдем координаты необходимых точек:
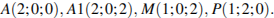

Если  — искомый угол, то:
— искомый угол, то:



Ответ: 
9. В правильной шестиугольной пирамиде МАBCDEF, стороны основания которого равны 1, а боковые ребра 4, найти синус угла между прямойВС и плоскостью EMD.
 Введем декартову систему координат, как показано на рис.
Введем декартову систему координат, как показано на рис.
Найдем координаты необходимых точек:
 ,
, 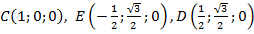 ,
, 
Выберем произвольную точку G в плоскости EMD, у которой будут не фиксированные координаты  ;
;
Затем находим необходимые для дальнейшего решения векторы
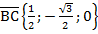 ;
;  ;
;  ;
;  ;
;
Теперь составим уравнение плоскости, проходящей через три точки
 = 0; Раскрываем определитель, раскладывая его по первой строке, и вычисляем полученные определители второго порядка
= 0; Раскрываем определитель, раскладывая его по первой строке, и вычисляем полученные определители второго порядка
x * 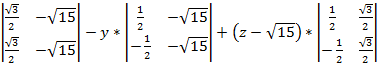 = 0
= 0
x*(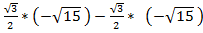 ) – y*(
) – y*( ) +
) +
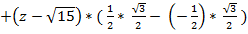 = 0
= 0
Раскрываем скобки и получаем уравнение плоскости

Следовательно, координаты нормального вектора заданной плоскости ─ 
Найдем синус угла между векторами 
 =
=  =
= 
Ответ:  =
= 
10. В кубе A…D1 определить угол между плоскостями ADD1 и BDC1.

 Решение: Пусть рёбра данного куба будут иметь длину, равную длине единичного вектора, тогда найдём координаты точек куба. D (0;0;0), A1 (1;0;1), D1 (0;0;1), B (1;1;0), C1 (0;1;1). Находим координаты векторов, принадлежащих данным плоскостям:
Решение: Пусть рёбра данного куба будут иметь длину, равную длине единичного вектора, тогда найдём координаты точек куба. D (0;0;0), A1 (1;0;1), D1 (0;0;1), B (1;1;0), C1 (0;1;1). Находим координаты векторов, принадлежащих данным плоскостям:
 |
1.  {1;0;1};
{1;0;1};
 {0;0;1);
{0;0;1);
2.  {0;1;1);
{0;1;1);
 {-1;-1;0}.
{-1;-1;0}.
Далее находим координаты векторов, перпендикулярных к данным плоскостям:
| i | j | k |
1.  =
=
 =i*(0)+j*(-1)+k*(0)
=i*(0)+j*(-1)+k*(0)
Откуда  {0;-1;0}.
{0;-1;0}.
| i | j | k |
2.  =
=
 =i*(-1)+j*1+k*(-1)
=i*(-1)+j*1+k*(-1)
Откуда  {-1;1;-1}.
{-1;1;-1}.
Теперь найдём косинус угла между нормалями:
| (-1)*0+1*(-1)+(-1)*0 |
 * * 
|

| |
cos(α)= ‘ sin(α)=

11. В единичном кубе A...D 1 найдите угол между плоскостями AED1 и FD1C, где F – середина ребра C1B1, а E – середина ребра A1B1
Решение: 
Нахождение угла между плоскостями AD1E и D1CF сводится к решению задачи на нахождение угла между нормалями соответствующих плоскостей.
1) Найдем координаты точек, необходимых для нахождения уравнения плоскости AD1E: 


2) Найдем уравнение плоскости AD1E и соответствующий ей вектор нормали плоскости:






 Уравнение плоскости
Уравнение плоскости

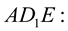 Вектор нормали плоскости
Вектор нормали плоскости
3) Найдем координаты точек, необходимых для нахождения уравнения плоскости D1FC:



4) Найдем уравнение плоскости D1FC и соответствующий ей вектор нормали плоскости:





 Уравнение плоскости
Уравнение плоскости

 Вектор нормали плоскости
Вектор нормали плоскости
5) Через скалярное произведение векторов вычислим косинус угла между векторами нормалей плоскостей:


Ответ:
12. В кубе A…D1 найдите синус угла между прямой A1D1 и плоскостью ACB1.
Решение. Пусть рёбра данного куба будут иметь длину, равную длине единичного вектора, тогда координаты точек куба A, C, B1, A1, D1 будут равны соответственно (1;1;0), (0;0;0), (0;1;1), (1;1;1), (1;0;1). Отсюда вектор A1D1 будет иметь координаты {0;-1;0}, а векторы  и
и  , принадлежащие плоскости, соответственно {0;1;1} и {1;1;0}. Находим вектор
, принадлежащие плоскости, соответственно {0;1;1} и {1;1;0}. Находим вектор  , являющийся нормалью к плоскости.
, являющийся нормалью к плоскости.
| i | j | k |
 =
=
 =i*(-1)+j*1+k*(-1)
=i*(-1)+j*1+k*(-1)
Таким образом, вектор  имеет координаты {-1;1;-1}. Подставляя полученные значения в формулу, получаем:
имеет координаты {-1;1;-1}. Подставляя полученные значения в формулу, получаем:
| (-1)*0+1*(-1)+(-1)*0 |
 * * 
|
sin(α)=



 |