ТРЕУГОЛЬНИКИ
Прямоугольные треугольники
| D |
| C |
| E |
| K |
1. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов (теорема Пифагора)
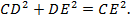
2. Синус острого угла прямоугольного треугольника равен отношению противолежащего этому углу катета к гипотенузе; косинус – отношению прилежащего катета к гипотенузе; тангенс – отношению противолежащего угла к прилежащему
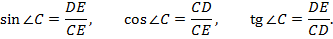
3. Площадь прямоугольного треугольника равна:
• половине произведения катетов
• половине произведения гипотенузы и проведенной к ней высоты;
• половине произведения гипотенузы, катета и синуса угла, заключенного между ними
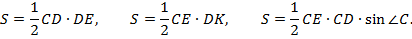
4. Синус одного острого угла прямоугольного треугольника равен косинусу другого его острого угла
5. Если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный (теорема, обратная теореме Пифагора).
№1. В треугольнике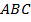 
, 
, 
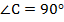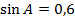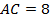. Найти 
.
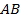№2. Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведенную к гипотенузе.
№3. В треугольнике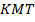 
, 
, 
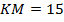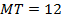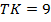. Найдите высоту треугольника, проведенную к его большей стороне.
Важные теоремы для произвольных треугольников
| C |
| D |
| E |
1. Теорема косинусов
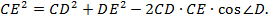
2. Теорема синусов
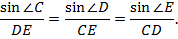
3. Теорема Герона
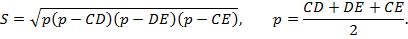
№4. В треугольнике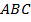 
, 
, 
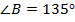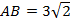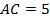. Найдите площадь треугольника.
№5. В треугольнике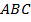 
, 
, 
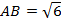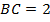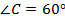. Найдите градусную меру угла 
.
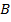№6. В треугольнике , ,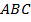 
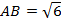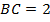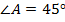. Найдите угол 
.
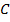№7. В треугольнике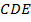 
, 
, 
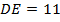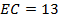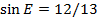. Найдите 
.
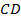Высота, медиана, биссектриса
1. В равностороннем треугольнике высота, медиана и биссектриса совпадают.
| A |
| N |
| B |
| M |
| C |
| K |
| O |
3. Все три медианы треугольника пересекаются в одной точке и делятся ею в отношении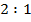 
, считая от вершины
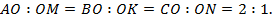
| A |
| B |
| A1 |
| C |
4. Все три биссектрисы треугольника пересекаются в одной точке, и каждая биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам
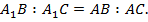
5. Медианы и биссектрисы всегда пересекаются во внутренней точке треугольника. Прямые, содержащие высоты остроугольного треугольника, пересекаются во внутренней точке, а тупоугольного – во внешней.
№8. Прямые, на которых лежат высоты треугольника 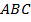пересекаются в точке 
, 
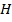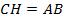. Найдите угол .
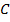№9. Площадь равнобедренного треугольника 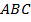с основанием 
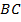равна 160, боковая сторона равна 20. Высоты 
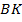и 
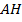пересекаются в точке 
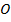. Найдите площадь треугольника 
.
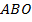№10. В треугольнике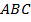 
, 
, 
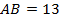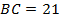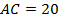. Найдите площадь треугольника, образованного стороной 
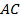, медианой 
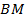и биссектрисой 
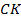данного треугольника.
Признаки равенства и подобия треугольников
1. Треугольник равны, если:
• две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника;
• сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника;
• три стороны одного треугольника равны трём сторонам другого
2. Треугольники подобны если:
• два угла одного треугольника соответственно равны двум углам другого;
• две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны;
• три стороны одного треугольника пропорциональны трём сторонам другого.
| B |
| H |
| A |
| C |
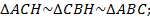
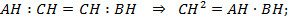
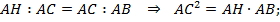
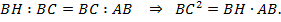
4. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
№11. На стороне 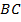треугольника 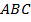отмечена точка 
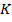. Известно, что
, 
, 
, 
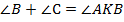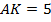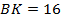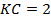. Найдите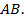 
№12. В остроугольном треугольнике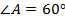 
, 
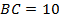, отрезк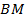и и 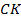– высоты. Найдите 
.
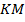№13. Из точки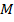 
катета 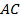прямоугольного треугольника 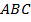проведен перпендикуляр 
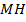к гипотенузе 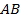. Найдите площадь треугольника 
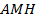, если 
, 
, 
.
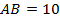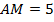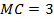№14. В треугольнике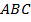 
, , 
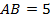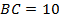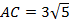. Найдите площадь треугольника, образованного высотой 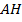, медианой 
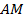и биссектрисой 
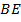данного треугольника.
№15. Сторона 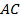треугольник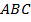а равна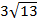 
. На стороне 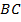отмечена точка 
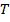так, что 
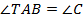. Найдите площадь треугольника 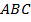, если 
, 
.
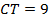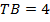Домашнее задание
| № | Ответ | № | Ответ |
| 0,25 | |||
| 17,6 | |||
| 10,5 |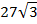 
| ||
| 
| ||
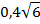
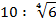
| 1,44 | |||
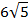
| 48; 20,25 | ||
| 1,6 | 16/3; 3 | ||
| 11/3 | |||
| |||
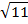
| 40,8 |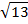 
| ||
| |||
|
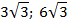
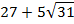