Введение
Рассматривается система стабилизации продольным движением судна на подводных крыльях на крейсерском режиме. Предполагается, что объект имеет два органа управления: носовые и кормовые закрылки. Провести параметрический синтез линейного оптимального регулятора. Критерий оптимальности синтеза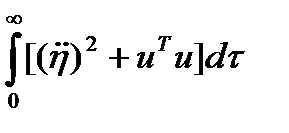 
.
Расчеты производиться при помощи программы Mathcad версии 11.
Техническое задание на проектирование.
1. Провести анализ свойств объекта управления при движении на крейсерском режиме.
2. Провести анализ управляемости и наблюдаемости (по всем фазовым переменным объекта). Рассчитать передаточные функции 
, 
от управляющих воздействий 
. Построить соответствующие ЛАЧХ и ЛФЧХ..
3. Провести предварительный расчет параметров линейного оптимального регулятора продольного движения.
4. Провести анализ движения объекта на регулярном встречном ветровом волнении (
). Волна описывается уравнением 
, где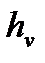 
- высота волны, 
- частота встречи объекта с волной (собственным движением волны пренебречь). Длину волны выбирать по высоте волны 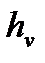в соответствии с бальностью волнения на глубокой воде. При расчете изменения угла дифферента принимать линейную аппроксимацию волнового фронта. Определить максимальный уровень волнения, при котором крылья не будут выходить из воды, волна не будет бить в корпус корабля, а максимальные перегрузки 
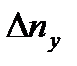не будут превышать 0.8g.
4. Провести моделирование линеаризованной системы с синтезированным регулятором. Рассчитать переходные процессы по фазовым координатам объекта. Рассмотреть режимы перехода на новый угол дифферента и новую высоту центра тяжести объекта при отсутствии волнения.
5. Провести моделирование линеаризованной системы с учетом ограничений на предельные отклонения управляющих органов (
).
6. Рассчитать дисперсии 
, 
и 
при воздействии ветрового волнения в виде случайного стационарного процесса с кажущимся спектром, определенного на предыдущем этапе допустимого волнения.
Описание объекта исследования с указанием всех его фазовых переменных, измеряемых выходов и управлений.
Рассматривается система стабилизации продольным движением судна на подводных крыльях на крейсерском режиме. Предполагается, что объект имеет два органа управления: носовые и кормовые закрылки. Скорость движения судна на крейсерском режиме составляет 20 м/с. Высота стоек подводных крыльев равна 1.8 м, расчетная глубина погружения крыльев составляет 0.9 м. Провести параметрический синтез линейного оптимального регулятора. Линеаризованная система описывается следующими уравнениями 
, где 
, 
. Здесь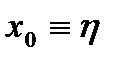 
(
- высота, в м., центра тяжести объекта над уровнем моря),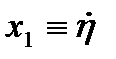 
, 
(
- угол дифферента в рад),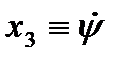 
. Управление 
- отклонение носового закрылка, 
- отклонение кормового закрылка. Критерий оптимальности синтеза 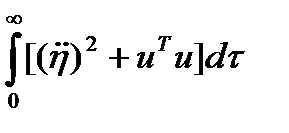. При расчете 
влиянием вектора 
пренебречь.
Линеаризованные уравнения имеют вид:
Исследование динамики объекта управления - расчетные характеристики, переходные процессы, управляемость, наблюдаемость, устойчивость.
Линеаризованная система описывается следующим уравнением:
,(4.1)
Применим к ней преобразование Лапласа, учитывая что начальные условия нулевые. Получим следующее матричное уравнение:
(4.2)
Передаточные функции , от управляющего воздействия , исходя из уравнения 4.2, будет иметь вид:
(4.3)
(4.4)
Передаточные функции , от управляющего воздействия , исходя из уравнения 4.2, будет иметь вид:
(4.5)
(4.6)
Реакция системы на функцию Хэвисайда поданную на .
(4.7)
(4.8)
Реакция системы на функцию Хэвисайда поданную на :
(4.9)
(4.10)
Реакция системы на функцию Дирака поданную на :
(4.11)
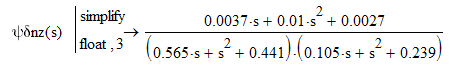(4.12)
Реакция системы на функцию Дирака поданную на :
(4.13)
(4.14)
Весовая функция высоты 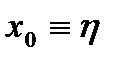рисунок 4.1 а) и угла дифферента рисунок 4.1 б) для управляющего воздействия :
Рисунок 4.1 Весовая функция а) высоты б) угла дифферента.
Весовая функция высоты 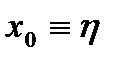рисунок 4.2 а) и угла дифферента рисунок 4.1 б) для управляющего воздействия :
Рисунок 4.2 Весовая функция а) высоты б) угла дифферента.
ЛАХЧ рисунок 4.3 а) и ЛФЧХ рисунок 4.3 б) высоты от управляющего воздействия
Рисунок 4.3 а)ЛАХЧ б) ЛФЧХ
ЛАХЧ рисунок 4.4 а) и ЛФЧХ рисунок 4.3 б) высоты от управляющего воздействия
Рисунок 4.4 а)ЛАХЧ б) ЛФЧХ
ЛАХЧ рисунок 4.5 а) и ЛФЧХ рисунок 4.3 б) угла дифферента от управляющего воздействия :
Рисунок 4.4 а)ЛАХЧ б) ЛФЧХ
ЛАХЧ рисунок 4.6 а) и ЛФЧХ рисунок 4.3 б) угла дифферента от управляющего воздействия :
Рисунок 4.6 а)ЛАХЧ б) ЛФЧХ
Исследуем наблюдаемость, составив матрицу наблюдаемости
, где 
(4.15)
(4.16)
Ранг матрицы максимален, следовательно система наблюдаема.
Исследуем управляемость системы, составив матрицу управляемости
(4.17)
(4.18)
Ранг матрицы максимален, следовательно система управляема.