Виды треугольников
Прямоугольный треугольник - это треугольник, в котором один угол прямой (т.е. 90°).
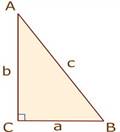∆ABC - прямоугольный (∠ACB = 90°);
AC, BC - катеты;
AB - гипотенуза.
Сторона прямоугольного треугольника, противолежащая прямому углу, наз. гипотенузой, две другие стороны наз. катетами.
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
a ² + b ² = c ², где
a, b - катеты;
c - гипотенуза.
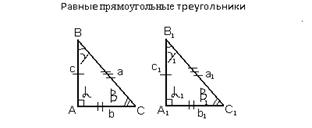Признаки равенства прямоугольных треугольников:
Два прямоугольных треугольника равны, если у них соответственно равны:
1. Гипотенуза и острый угол.
2. Катет и противолежащий угол.
3. Катет и прилежащий угол.
4. Два катета.
5. Гипотенуза и катет.
Подобие в прямоугольных треугольниках.
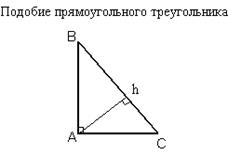
Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:
1. Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому (Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось.) проекций катетов на гипотенузу.
2. Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.
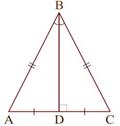Равнобедренный треугольник – это треугольник, у которого 2 стороны равны. Эти стороны наз. боковыми, а третья сторона – основанием.
Свойства равнобедренного треугольника.
1) В равнобедренном треугольнике углы при основании равны.
Доказательство
Пусть Δ ABC – равнобедренный с основанием AB. Рассмотрим Δ BAC. По первому признаку эти треугольники равны. Действительно, AC = BC; BC = AC; C = C. Отсюда следует A = B как соответствующие углы равных треугольников
2) В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Доказательство
Пусть Δ ABC – равнобедренный с основанием AB, и CD – медиана, проведенная к основанию. В треугольниках CAD и CBD углы CAD и CBD равны, как углы при основании равнобедренного треугольника (по теореме 4.3), стороны AC и BC равны по определению равнобедренного треугольника, стороны AD и BD равны, потому что D – середина отрезка AB. Отсюда получаем, что Δ ACD = Δ BCD.
Из равенства треугольников следует равенство соответствующих углов: ACD = BCD, ADC = BDC. Из первого равенства следует, что CD – биссектриса. Углы ADC и BDC смежные, и в силу второго равенства они прямые, поэтому CD – высота треугольника
Признаки равнобедренного треугольника.
1) Если в треугольнике два угла равны, то он равнобедренный.
2) Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
3) Третий признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
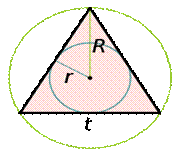
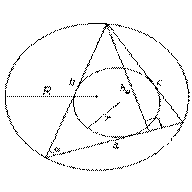
Правильный треугольник – треугольник, у которого все стороны равны
a — сторона правильного треугольника,
R — радиус описанной окружности,
r — радиус вписанной окружности.
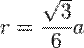- радиус вписанной окружности правильного треугольника, выраженный через его сторону
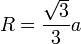- радиус описанной окружности правильного треугольника, выраженный через его сторону
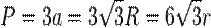- периметр правильного треугольника равен
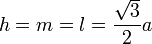- высоты, медианы и биссектрисы правильного треугольника
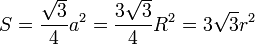- площадь правильного треугольника
R=2r - радиус описанной окружности равен двойному радиусу вписанной окружности
Остроугольный треугольник – треугольник, у которого все три угла — острые, то есть меньше 90°.
Тупоугольный треугольник – треугольник, у которого один из углов — тупой, то есть больше 90°.
Основные линии треугольника
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника.
Свойства медиан треугольника
· 1) Медиана разбивает треугольник на два треугольника одинаковой площади.
2) Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины.
3) Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
4) 
Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектриса треугольника - отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрис треугольника
1) Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
2) Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам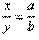 
3) Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
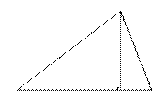Высота треугольника - перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.
Свойства высот треугольника
1) В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
2) В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
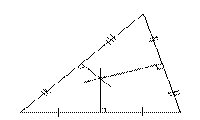Срединный перпендикуляр к отрезку - прямая, проходящую через середину отрезка перпендикулярно к нему.
Свойства серединных перпендикуляров треугольника
1) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
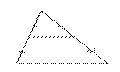2) Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
Средняя линия треугольника - отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Признаки равенства треугольников:
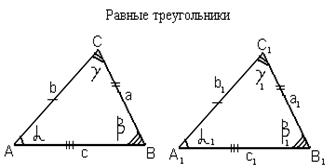
1) Три стороны одного треугольника равны трем сторонам другого треугольника (по трем сторонам).
2) Две стороны одного треугольника равны двум сторонам другого треугольника и углы между этими сторонами также равны (по двум сторонам и углу между ними).
3) Три угла одного треугольника равны трем углам другого треугольника (по трем углам).
4) Два угла одного треугольника равны двум углам другого треугольника, и любая сторона первого треугольника равна соответствующей стороне другого треугольника.
Подобные треугольники
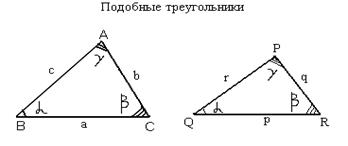Два треугольника являются подобными, если углы одного треугольника равны, углам другого треугольника, а стороны подобны, т.е.
(р/а)=(q/b)=(r/c).
Признаки подобия треугольников:
1) Два угла одного треугольника равны двум углам другого треугольника.
2) Две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны.
3) Три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.
Свойства подобных треугольников
1) Отношение площадей подобных треугольников равно квадрату коэффициента подобия [(р/а)=(q/b)=(r/c)=коэффициент подобия].
2) Отношение периметров и длин либо биссектрис, либо медиан, либо высот, либо серединных перпендикуляров равно коэффициенту подобия. т.е. в подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.
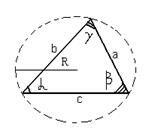
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности:
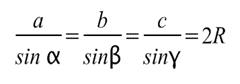
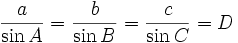
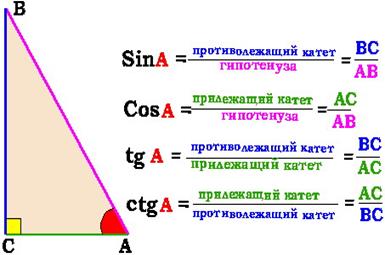
Синус - это отношение противолежащего катета (катета который лежит против угла, синус которого необходимо найти), к гипотенузе данного треугольника.
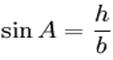
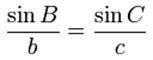
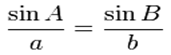
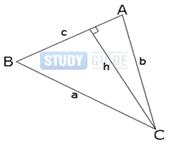
Теорема косинусов
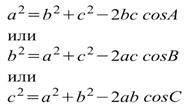Косинус - это отношение прилежащего катета (катета который лежит при угле, косинус которого необходимо найти), к гипотенузе данного треугольника.
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
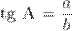
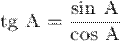
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):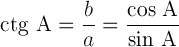 
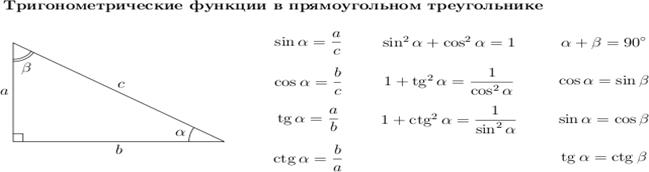
Формулы площади треугольника