Методика построения графика обратной функции

Лекция №12

ГЛАВА V. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Понятие функции. Способы задания функции. Обратная функция

 

I. Определение. Пусть даны два непустых множества D и E.

x

D

f

y

E

 

 

def. Если каждому элементу по определенному правилу (закону) f ставится в соответствие единственный элемент , то говорят, что на множестве D задана функция

Если D и E – числовые множества то числовая функция.

Принята следующая терминология:

x – независимая переменная или аргумент;

y – зависимая переменная;

D – область определения функции;

Е – множество значений функции.

Если каждому элементу соответствует не одно, а несколько значений , то получим многозначную функцию (не рассматриваем).

Под функцией будем понимать однозначную числовую функцию.

При конкретном значении аргумента получим частное значение функции или .

 

II. Способы задания функции

1. Аналитический. Явное и неявное задание функции

Функция задается аналитическим выражением, т.е. формулой.

Пример 1.1. а) б)

Нельзя отождествлять функцию и формулу: с помощью одной формулы можно задать различные функции (указывая различные области определения), и наоборот, одна функция может быть задана несколькими формулами.

явное задание функции.

Пример1.2.

неявное задание функции.

Пример 1.3. а)

б) (здесь можно перейти к явному).

Преимущества: удобно изучать свойства. Недостатки: малая наглядность.

1. Табличный

В таблице указывается в определенном порядке значения аргумента и соответствующие значения функции.

x	x1	x2	…	xn
y	y1	y2	…	yn

Пример1.4. Таблицы тригонометрических функций.
Преимущества: Без вычислений находятся соответствующие значения функции.

Недостатки: не можем получить значений y, неуказанных в таблице.

1. Графический

Функция представляется графиком.

Пример1.5. Графики, полученные с помощью самопишущих приборов, например, электрокардиограмма (кривая изменения электрических импульсов сердечной мышцы, вычерчиваемая электрокардиографом); барограммы (кривые зависимости между давлением и временем в метеорологии).

Преимущества: наглядность.

Недостатки: неточность, неудобен при применении математического аппарата.

1. Программный

Функция задается с помощью указания программы на одном из машинных языков.

III. Обратная функция

Функция 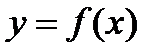является отображением .

Рассмотрим взаимнооднозначное отображение (взаимно однозначную функцию).

взаимно однозначная функция.

x

y

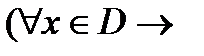ед. 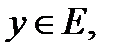и обратно, 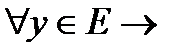ед. ).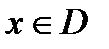

Пример 1.6.

 

а) - взаимно однозначная функция

(отображение)

 

 

x

y

 

б) не является взаимно однозначной.

 

Пусть 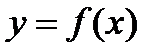() – взаимно однозначное отображение. Значит, ставится в соответствие ед. . Тогда говорят, что на множестве Е определена функция, обратная функции 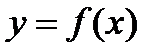, которая обозначается

 

Теорема. Если 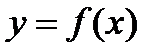монотонная функция (возрастает или убывает), то существует обратная функция 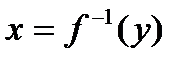. При этом, если f – возрастающая, то f^-1 – возрастающая; если f – убывающая, то и f^--1 – убывающая.

 

Методика построения графика обратной функции

 

1) 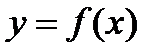монотонная на D(f).

2) Решаем 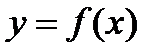относительно x, т.е. находим 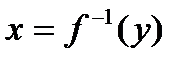(по существу 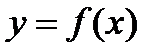и 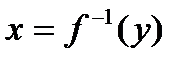выражают одну и ту же зависимость, графики совпадают).

3) Переобозначаем переменные, т.е. - обратная функция.

x

y

0

1

1

-1

-1

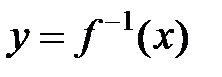4) График симметричен графику 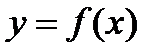относительно биссектрисы первого координатного угла.

Пример1.7. возраcтает на D=R;

обратная функция.

 

IV. Основные элементарные функции. Самостоятельно. Графики функций:

1) постоянная y=c;

2) степенная

а) б) в) г)

3) показательная . а) б)

4) логарифмические:

5) тригонометрические:

6) обратные тригонометрические функции:

x y 0 1 -1	x y 0 1 -1
x y 0	x y 0