Отчет по лабораторной работе №7
«Синтез информационной сети древовидной структуры.
Древовидные сети»
Выполнил: Белов В.А.
Акимов А.С.
Группа ИСТ-92
Проверил: Тарасов В.А.
Санкт-Петербург
2012 г.
1. Цель:
Ознакомление с методами анализа и синтеза централизованных информационных сетей.
2. Математическая постановка задачи:
Алгоритмы определения оптимальной структуры при наличии ограничений для сети большой размерности требуют значительных затрат времени вычисления. Поэтому на практике применяются эвристические алгоритмы, которые позволяют найти решения, близкие к оптимальным, при значительном уменьшении объема вычислений.
Рассмотрим следующие эвристические алгоритмы построения информационных сетей древовидной структуры: алгоритм Прима, алгоритм Краскала, алгоритм Ежи-Вильямса. В основе алгоритма Ежи-Вильямса лежит процедура поиска наиболее удаленных узлов (в смысле стоимости) и соединения их с соседними узлами с целью обеспечения наибольшего выигрыша по стоимости. При использовании алгоритма Прима производятся обратные действия: вначале выбираются узлы, ближайшие к центру, затем к этим узлам подключаются ближайшие и т.д. По алгоритму Краскала последовательно выбираются линии с наименьшей стоимостью.
2.1 Алгоритм Прима.
Шаг 0. Каждому узлу приписывается вес Wi. При этом W1=0 (центральный узел), все остальные Wi равны бесконечности, i>1. Затраты Тij определяются следующим образом:
Sij-Wi, Sij - стоимость подключения пункта 1 к пункту j. Первоначально вcе Тij равны бесконечности, кроме Т1j.
Шаг 1. Найти минимальное значение Тij для узлов, которые еще не включены в сеть.
Шаг 2. Проверка ограничений по пропускной способности каналов связи. Если ограничения выполняется, перейти к шагу 3, иначе вернуться к шагу 1.
Шаг 3. Включить линию. ij в структуру сети, установит Wj=0, изменить исходные условия и заново вычислить все Tij. Вернуться к шагу 1.
2.2 Алгоритм Краскала.
Шаг 1. Выбирается линия ij с наименьшей стоимостью.
Шаг 2. Проверка ограничений по пропускной способности к отсутствию циклов.
Шаг 3..Включить линию ij в структуру сети.
Алгоритм повторяется до тех пор, пока все узлы не будут включены в сеть.
2.3. Алгоритм Ежи-Вильямса.
Шаг 0. Вычисление всех параметров затрат  для всех i,j >1, где Sij - соответствующий элементам матрицы стоимости.
для всех i,j >1, где Sij - соответствующий элементам матрицы стоимости.
Шаг 1. Выбрать минимальное 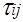 .
.
Шаг 2. Проверка ограничений. Если ограничения выполняются, то перейти к шагу 3. Если нет, то положить 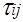 равным бесконечности н вернуться к шагу 1.
равным бесконечности н вернуться к шагу 1.
Шаг 3. Добавить линию ij, изменить исходные условия (учесть потоки), вернуться к шагу 1.
Использование эвристических алгоритмов является компромиссом между стремлением улучшить качество, сети и объемом вычислений.
3. Исходные данные:
Дано 10 городов: Riga (4), Helsinki (4), Brussel (8), Stokholm (5), Minsk (4), Frankfurt (3), Amsterdam (8), Wien (5), Berlin (7), Warshau (6).
Оптимальная цена: 133081
Оптимальная задержка: 10.1161
4. Структура сети:
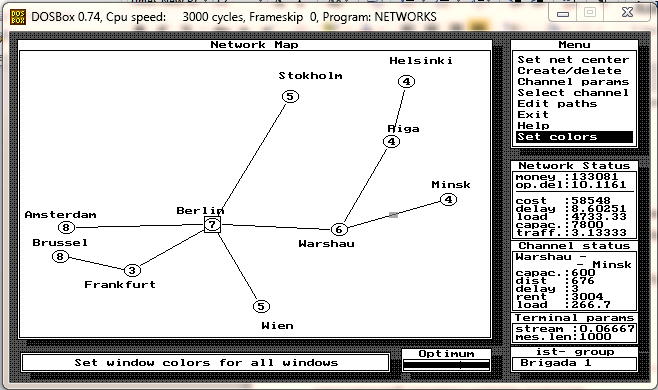
5. Пропускная способность каналов:
| Канал | Пропускная способность |
| Берлин – Стокгольм | |
| Берлин – Франкфурт | |
| Берлин – Вена | |
| Берлин – Варшава | |
| Варшава – Рига | |
| Франкфурт – Брюссель | |
| Варшава – Минск | |
| Берлин – Амстердам | |
| Рига – Хельсинки |
6. Стоимость и задержки сети:
| Канал | Стоимость | Задержки |
| Берлин – Стокгольм | 3.75 | |
| Берлин – Франкфурт | ||
| Берлин – Вена | 3.75 | |
| Берлин – Варшава | 0.8333 | |
| Варшава – Рига | 2.727 | |
| Франкфурт – Брюссель | ||
| Варшава – Минск | ||
| Берлин – Амстердам | ||
| Рига – Хельсинки | ||
| Всего | 8.60251 |
Результаты лучше, нежели минимально необходимые.
Вывод:
В ходе данной лабораторной работы были изучены методы анализа и синтеза древовидных информационных сетей. Были подобраны такие параметры, чтобы они соответствовали, или были лучше, чем минимальные.