Лекция 3
Распределение света по оптическому волокну
План:
1. Лучевой подход;
2. Электромагнитный подход;
3. Волновой анализ распространения света в волокне;
4. Распространение различных мод по оптоволокну;
5. Связь между понятиями луча и моды.
Оптические волны распространяются в ОВ при выполнении условий n1 > n2. соотношение между n1 > n2, принято характеризовать разностью показателей преломления Δ= (n1 > n2)/ n1. для большинства ОВ Δ = 0.01...0.001.
Показатель преломления оболочки имеет постоянное значение, а показатель преломления сердцевины может оставаться постоянным или изменяться вдоль радиуса по определенному закону. Изменение показателей преломления ОВ вдоль радиуса называется профилем показателя преломления.
Исходя из двойственной природы света, процесс распространения светового излучения в световодах можно изучать, используя методы геометрической оптики (лучевой подход) или волновые уравнения ЭМ поля (ЭМ подход).
Лучевой подход
Основная его идея заключается в том, что в оптическом диапазоне частот с достаточно большой точностью распространение волн можно представить как движение энергии волн по лучам, описываемым с помощью геометрических соотношений. Анализ распространения света в лучевом приближении составляет предмет геометрической оптики.
Необходимым условием распространения света в ОВ в рамках лучевого подхода является требование падения лучей на торец ОВ в пределах входной угловой апертуры. Однако это условие не является достаточным, так как только часть из этих лучей будут распространяться вдоль оси световода.
Лучевой подход основан на представлении источника излучения и светового луча соответственно в виде точки и линии (рисунок 3.1).

Рисунок 3.1 - Полное внутреннее отражение света на границе вода–воздух;
S – точечный источник света
Лучевой подход наглядно показывает процессы распространения света по световодам, однако им можно пользоваться только при соблюдении условия малости длины волны по сравнению с радиусом сердцевины волокна. Поэтому лучевой моделью можно пользоваться при изучении распространения света в многомодовых волокнах, где указанное условие соблюдается.
Свет, попадающий на торец световода, может распространяться по нему на большие расстояния за счет полного внутреннего отражения от боковых поверхностей (рисунок 3.2). Научно-техническое направление, занимающееся разработкой и применением оптических световодов, называется волоконной оптикой.
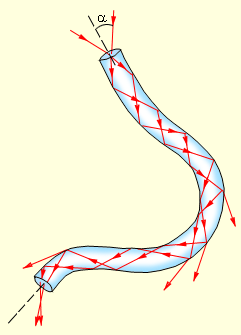
Рисунок 3.2 - Распространение света в волоконном световоде.
При сильном изгибе волокна закон полного внутреннего отражения нарушается, и свет частично выходит из волокна через боковую поверхность
Напомним основные законы геометрической оптики:
1. Отражение света. Когда свет падает на границу раздела двух сред, определённая его часть отражается. Количество отражённого света зависит от угла α1 между падающим лучом света и нормалью к поверхности падения. Термин "луч света" здесь используется для обозначения пути, по которому проходит световая энергия. Для отражённого луча и угла α2, образованного нормалью к поверхности падения и отражённым лучом света (рисунок 3.3), имеют силу следующие утверждения:
Отражённый луч:
- остаётся в плоскости падения, образуемой падающим лучом света и нормалью к поверхности падения луча;
- по отношению к падающему лучу света лежит на противоположной стороне от нормали к поверхности падения луча;
- имеет угол отражения по отношению к нормали к поверхности падения, равный углу падения.
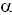 1 =
1 = 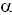 2. (3.1)
2. (3.1)
2. Преломление света. Когда луч света входит под углом падения α в оптически более плотную среду (например, стекло или воду) из оптически менее плотной среды (например, воздуха), то его направление распространения по отношению к нормали к поверхности падения изменяется, он преломляется под углом преломления β.
Для изотропной среды, то есть материала или вещества, имеющего одинаковые свойства во всех направлениях, применим закон преломления Снеллиуса (1621г.): отношение угла падения к синусу угла преломления является величиной постоянной и также идентично отношению с1/с2 скоростей света с1 в первой среде и с2 во второй среде (рисунок 3.4)
 , (3.2)
, (3.2)
где α – угол падения; с1 – скорость света 1; β – угол преломления; с2 – скорость света 2.
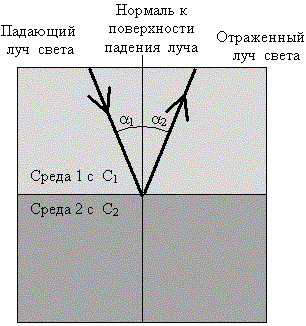
Рисунок 3.3 – Отражение света

Рисунок 3.4 – Преломление света
Из двух оптических сред более плотной называется та, в которой скорость света меньше.
При переходе из вакуума (воздуха), где свет распространяется со скоростью со, в среду со скоростью света с имеет силу отношение
 . (3.3)
. (3.3)
Отношение скорости света со в вакууме к скорости света с в среде называется показателем преломления n (более точно, фазовым показателем преломления) соответствующей среды. Показатель преломления вакуума (воздуха) no=1.
Для двух различных сред с показателями преломления n1 и n2 и скоростями света в них c1 и c2 имеют силу следующие соотношения:
c1=co/n1 и c2=co/n2. (3.4)
Отсюда следует еще одна форма закона Снеллиуса - отношение синуса угла падения к синусу угла преломления равно обратному отношению соответствующих показателей преломления:
 . (3.5)
. (3.5)
3. Полное внутреннее отражение. Если луч света (3) падает на поверхность раздела между средой с показателем преломления n1 и средой с показателем преломления n2<n1 под постепенно уменьшающимся углом, то есть с постепенно увеличивающимся углом падения 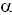 , то при определенном угле падения
, то при определенном угле падения 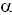 о угол преломления становится равным βо = 90о (рисунок 3.5).
о угол преломления становится равным βо = 90о (рисунок 3.5).

Рисунок 3.5 – Полное внутреннее отражение:
1' – полностью отраженный луч света; 2' – преломленный луч света с углом преломления β0=90; 3' – преломленный луч света
В этом случае луч света (2') распространяется параллельно поверхности раздела двух сред. Угол падения 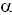 о называется критическим (предельным) углом двух сред. Для критического угла
о называется критическим (предельным) углом двух сред. Для критического угла 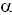 о имеет силу следующее соотношение:
о имеет силу следующее соотношение:
sin 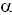 о = n2 / n1,
о = n2 / n1,
то есть критический угол зависит от отношения показателей преломления n1 и n2 двух сред. Например, для критического угла между водой с n1=1,333 и воздухом с no=1 имеем sin 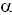 о=1/1,333
о=1/1,333  0,75 и
0,75 и 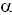 о
о  49о; между стеклом с n1=1,5 и воздухом с no=1 он равен sin
49о; между стеклом с n1=1,5 и воздухом с no=1 он равен sin 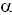 о=1/1,5
о=1/1,5  0,67 и
0,67 и 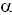 о
о  42о.
42о.
Для всех лучей, у которых угол падения 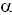 больше критического угла
больше критического угла 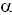 о, не существует соответствующих преломленных лучей в оптически менее плотной среде. Эти лучи света отражаются на поверхности раздела обратно в оптически более плотную среду - это явление называется полное внутреннее отражение (луч света 1).
о, не существует соответствующих преломленных лучей в оптически менее плотной среде. Эти лучи света отражаются на поверхности раздела обратно в оптически более плотную среду - это явление называется полное внутреннее отражение (луч света 1).
Полное внутреннее отражение может происходить на поверхности раздела сред только тогда, когда луч света распространяется из оптически более плотной среды (например, стекло n1=1,5) в оптически менее плотную среду (например, воздух no=1), и никогда не происходит в обратном случае.
У реальных ОВ, вследствие малой разности показателей преломления сердцевины п1 и оболочки п2, луч света проникает, а следовательно и распространяется по оболочке ОВ даже при углах падения φi > φпр, см. рисунок 3.6. Глубина проникновения волн в оболочку уменьшается при увеличении угла падения, при этом отраженная волна приобретает фазовый сдвиг, зависящий от угла падения. Глубина проникновения (δ), т.е. расстояние, на котором плоская волна ослабевает в е = 2,71 раза при φi > φпр определяется выражение:
 (3.6)
(3.6)
где λ — длина волны.
Полное внутреннее отражение плоской волны на границе раздела двух сред сопровождается теми же эффектами, что и отражение от металлической плоскости, смещенной на некоторое расстояние λ 0 от поверхности раздела. Поток энергии из первой среды во вторую в среднем равен нулю, поэтому энергия падающей ЭМ волны полностью возвращается в первую среду при условии отсутствия потерь энергии во второй среде.

Рисунок 3.6 - Скачок фазы на границе раздела двух сред
Электромагнитный подход
Для расчета ЭМ процессов в световодах используют ряд математических моделей, отличающихся друг от друга сложностью математического аппарата и наглядностью. В первую очередь стремятся использовать наиболее простые в математическом плане модели, обладающие наибольшей наглядностью. При необходимости учета более сложных деталей процесса распространения света в световоде переходят к использованию более сложных математических моделей.
В случае одномодовых волокон требуется ЭМ подход, т.е. решение волновых уравнений при заданных граничных условиях.
Электромагнитный подход позволяет точно рассчитать число мод (лучей), которые могут распространяться по световоду. Расчет подразумевает совместное решение волновых уравнений для сердцевины и оболочки оптического волокна с учетом граничных условий.
Для того, чтобы не делать расчет для каждого световода отдельно, а получить характеристики, присущие определенному типу световодов (например, для ступенчатого профиля), вводят понятие нормированной (характеристической) частоты. Нормированная частота является обобщенной характеристикой световода, поскольку зависит не только от геометрических и оптических характеристик световода, но и от длины волны источника излучения.
Типы и число направляемых волн (мод). Для правильной эксплуатации волоконных световодов, а также нормирования разброса длин волн лазерных источников излучения, необходимо знать наименьшую эксплуатационную длину волны, называемую критической длиной волны волоконного световода, при которой может распространяться только одна фундаментальная мода. Один и тот же световод для длин волн, выше критической длины волны, работает в одномодовом режиме, а для длин волн ниже критической длины волны работает в многомодовом режиме.
При лучевом подходе каждой из этих мод соответствует меридиональный луч с определенным углом наклона к оси волокна.
Важным параметром любой моды является ее частота отсечки (fкрmn), называемая также критической частотой, ниже которой поле не распространяется вдоль световода.
В случае симметричных мод для определения частот отсечки можно воспользоваться уравнением
 . (3.7)
. (3.7)
которое имеет бесчисленное множество решений (корней).
Достоинством одномодовой передачи является широкая полоса передаваемых частот (несколько гигагерц) и меньшее затухание по сравнению с многомодовой. С увеличением числа мод полоса передаваемых частот сужается. Однако одномодовый режим требует применения когерентных источников излучения (лазеров). Для многомодовых систем передачи можно использовать простейшие источники излучения — светодиоды.
Число мод (N) при ступенчатом профиле показателя преломления приблизительно равно
 . (3.8)
. (3.8)
Из выражения (3.8) видно, что значение V может быть уменьшено за счет уменьшения диаметра сердцевины и разности показателей преломления и увеличения рабочей длины волны.
Число направляемых мод градиентного волокна равно
 . (3.9)
. (3.9)
При одинаковой нормированной частоте число направляемых мод градиентного ОВ в 2 раза меньше, чем у ступенчатого, что существенно улучшает его характеристики передачи.
Когда нормированная частота при ступенчатом профиле световода меньше критического значения Vc= 2,405, волокно поддерживает распространение только одной фундаментальной моды. Волокно, в котором может распространяться только фундаментальная мода, называется одномодовым. Вследствие поляризации света фундаментальная мода может существовать в двух ортогональных поляризациях. Влияние поляризации необходимо учитывать при скорости передачи 2,5 Гбит/с и выше.
Волновой анализ распространения света в волокне
Количественный анализ ЭМ процессов проводится на основе уравнений Максвелла. Волновые уравнения получаются из уравнений Максвелла и характеризуют закон изменения векторов напряженности электрического и магнитного поля для гармонических процессов. Простейшим случаем волнового процесса является плоская волна. Плоской называют такую волну, при которой в ЭМ поле можно провести ряд параллельных плоскостей, перпендикулярных направлению распространения волны так, чтобы вектора Е и Н — общепринятое обозначение соответственно векторов электрического и магнитного поля — лежали в этих плоскостях и сохраняли как свое значение, так и направление вдоль всей плоскости. Так как волновые уравнения линейны, то общее решение уравнения является суперпозицией всех плоских волн, распространяющихся в любых направлениях. Понятие плоской волны при изучении ЭМ волн имеет такое же фундаментальное значение, как и гармонических (синусоидальных) колебаний при изучении изменяющихся во времени сложных процессов.
Рассмотрим волновые процессы в идеальном ОВ двухслойной конструкции (см.рисунок 3.7)без потерь.
В цилиндрической системе координат волновые уравнения для продольных составляющих ЕZ и НZ для сердцевины (r<а) имеют вид
 ; (3.10)
; (3.10)
 ; (3.11)
; (3.11)
 , (3.12)
, (3.12)
поскольку в случае диэлектрических материалов ε =  , μ=μ0 и в средах без потерь γ2 = - β2 (β — продольный коэффициент распространения волны в ОВ).
, μ=μ0 и в средах без потерь γ2 = - β2 (β — продольный коэффициент распространения волны в ОВ).

Рисунок 3.7 – Волновые процессы в идеальном оптическом волокне
Фазовая постоянная распространения плоских волн β1 в среде с показателем преломления п1 определяется в случае однородного диэлектрика соотношением
 .
.
где εr1 -относительная диэлектрическая проницаемость сердцевины ОВ; λ — длина волны в вакууме; п1 — коэффициент преломления сердцевины волокна ОВ относительно вакуума или показатель преломления сердечника; с — скорость света в вакууме.
Для рассмотрения процессов в оболочке (r  а) воспользуемся теми же уравнениями (3.10) и (3.11) с заменой g1 на g2.
а) воспользуемся теми же уравнениями (3.10) и (3.11) с заменой g1 на g2.
g22 =ω2μоε2 — β2 = β22 — β2, (3.13)
где β 2 = 2 πn 2/ λ — фазовая постоянная распространения плоских волн в среде с диэлектрической проницаемостью, равной ε2, и соответственным показателем преломления п2 = 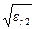 .
.
Уравнения (3.10) и (3.11) однотипны, поэтому поясним подход к их решению на примере уравнения (3.10) для продольных составляющих Ez.
В соотношениях между цилиндрическими функциями, с одной стороны, и показательной и тригонометрической функциями с другой имеется некоторая аналогия.
Известные соотношения между последними
 ; (3.14)
; (3.14)
 (3.15)
(3.15)
похожи на соотношениядля цилиндрических функций
 ; (3.16)
; (3.16)
 . (3.17)
. (3.17)
Переменная z может быть произвольной комплексной величиной. Если переменная z = х вещественна, то функции Бесселя первого Jm(x) и второго Nm(x) родов имеют, как и тригонометрические функции, осциллирующий характер. При z → 0 только функция Jm(z) остается конечной. Функции Ганкеля напоминают показательные функции, а именно функция Нm(1) (z) для больших значений аргумента z уменьшается экспоненциально так же, как показательная функция еjх, если z = х +jy имеет положительную мнимую часть. Если же z = x—jy, то функция Нm(2) (z) будет убывать подобно функции e-jz. Отмеченные аналогии функций, выражающих волновые процессы при плоских и цилиндрических волнах, сведены в таблице 3.1.
Выбор вида цилиндрических функций, описывающих электромагнитное поле в сердцевине и оболочке, определяется физическими соображениями передачи направляемых мод и предельными значениями цилиндрических функций.
Таблица 3.1
| Плоские волны | Цилиндрические волны |
Бегущие 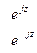 Стоячие
Стоячие 
| Нm(1) (z) – функция Ганкеля I рода Нm(2) (z) – функция Ганкеля II рода Jm(x) – функция Бесселя I рода Nm(x) – функция Бесселя II рода или Неймана |