Лекция 3. Диэлектрики и проводники в
электростатическом поле
План лекции
3.1. Поляризация диэлектриков.
3.2. Проводники в электростатическом поле.
3.3. Электроемкость проводника. Конденсаторы.
3.4. Энергия заряженных тел. Энергия электростатического поля
Поляризация диэлектриков
При изучении поведения различных веществ в электростатическом поле одним из основных является понятие «электрический диполь », так как образующие вещество атомы и молекулы в большинстве случаев представляют собой как раз такие объекты. Электрический диполь (рис.3.1) - это система двух равных по модулю разноименных точечных зарядов (+ Q, - Q), расстояние между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя от отрицательного заряда к положительному и равный по модулю расстоянию между ними называют плечом диполя 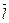 . Вектор
. Вектор
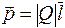 , (3.1)
, (3.1)
называют электрическим моментом диполя или дипольным моментом. Молекулы, составляющие диэлектрик в целом электрически нейтральны. Если заменить положительные заряды ядер молекул суммарным зарядом "+ Q ", находящимся в центре «тяжести» положительных зарядов, а заряды всех электронов суммарным отрицательным зарядом "- Q ", находящимся в центре «тяжести» отрицательных зарядов, то молекулу можно рассматривать как электрический диполь.
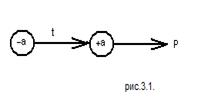
Рис.3.1
Как правило, в отсутствие внешнего электростатического поля суммарный дипольный электрический момент диэлектрика равен нулю. Поляризацией называется процесс возникновения в диэлектрике (при внесение его в электрическое поле) отличного от нуля результирующего дипольного момента. Естественно, что специфика процесса поляризации диэлектрика обуславливается особенностями его молекулярного строения. Так, например, у веществ, в молекулах которых совпадают центры «тяжести» положительных и отрицательных зарядов, в отсутствии внешнего электростатического поля дипольный момент равен нулю. Молекулы таких диэлектриков называются неполярными. Это, например N2; H2; O2; CO2. Под действием внешнего электростатического поля в молекулах происходит деформация электронных орбит и появляется отличный от нуля дипольный момент. Такая поляризация называется электронной или деформационной.
Существует и другая группа диэлектриков (Н2О; NH3; SO2, СО2), у молекул которых центры «тяжести» положительных и отрицательных зарядов не совпадают. Эти молекулы и в отсутствии внешнего электростатического поля обладают дипольным моментом. Такие молекулы называются полярными. При отсутствии внешнего электростатического поля вследствие хаотического теплового движения дипольные моменты полярных молекул диэлектрика ориентированны хаотически и их результирующий дипольный момент равен нулю. При внесении такого диэлектрика во внешнее электростатическое поле силы поля стремятся развернуть диполи вдоль поля и возникает преимущественная ориентация дипольных моментов («вдоль поля») и следовательно, - отличный от нуля результирующий дипольный момент. Такая поляризация диэлектриков называется ориентационной (или дипольной).
Третью группу диэлектриков составляют ионные кристаллы (NaСl, КСl, KBr...). В кристаллических решетках таких веществ симметрично чередуется разноименно заряженные ионы. В такой структуре не возможно выделить отдельные молекулы, и ее обычно рассматривают как систему двух вдвинутых в друг в друга ионных подрешеток.
При помещении такого кристалла в электростатическое поле происходит относительное смещение подрешеток (положительной - вдоль поля, отрицательной - против), приводящем к возникновению дипольного момента. Такая поляризация диэлектриков называется ионной.
Количественной характеристикой поляризации является поляризованность 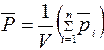 , (3.2)
, (3.2)
где 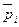 - дипольный момент одной молекулы; V -объем диэлектрика. Из (3.2) следует, что поляризованность определяется дипольным моментом единицы объема диэлектрика, т.е.при V = 1:
- дипольный момент одной молекулы; V -объем диэлектрика. Из (3.2) следует, что поляризованность определяется дипольным моментом единицы объема диэлектрика, т.е.при V = 1:
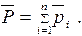
Для большинства изотропных диэлектриков
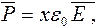 (3.3)
(3.3)
где х - диэлектрическая восприимчивость характеризует свойства диэлектрика (х - безразмерная величина).
Для установления количественных соотношений для электрического поля в диэлектрике рассмотрим поле двух бесконечных, параллельных, равномерно заряженных плоскостей с разноименными зарядами, с напряженностью 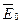 , в которое помещена диэлектрическая пластина толщиной " d " (рис. 3.2). Под действием поля в диэлектрике происходит смещение зарядов (появляется дипольный момент) и диэлектрик поляризуется. На гранях диэлектрика появляется избыток зарядов, с поверхностными плотностями
, в которое помещена диэлектрическая пластина толщиной " d " (рис. 3.2). Под действием поля в диэлектрике происходит смещение зарядов (появляется дипольный момент) и диэлектрик поляризуется. На гранях диэлектрика появляется избыток зарядов, с поверхностными плотностями 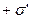 и
и 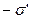 . Эти заряды, появляющиеся в результате поляризации диэлектрика, называют связанными. Их поверхностная плотность
. Эти заряды, появляющиеся в результате поляризации диэлектрика, называют связанными. Их поверхностная плотность  меньше плотности
меньше плотности  свободных зарядов плоскостей, поэтому поле свободных зарядов Е 0 частично компенсируется полем связанных зарядов
свободных зарядов плоскостей, поэтому поле свободных зарядов Е 0 частично компенсируется полем связанных зарядов 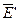 и внутри диэлектрика устанавливается результирующее поле
и внутри диэлектрика устанавливается результирующее поле
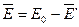 . (3.4)
. (3.4)
Согласно (1.13) поле двух бесконечно заряженных плоскостей  и (3.4) принимает вид
и (3.4) принимает вид
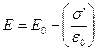 . (3.5)
. (3.5)

Рис.3.2
Если рассматривать диэлектрик как диполь, то, в соответствии с (3.1) и(3.2), его дипольный момент можно записать в виде  (S - площадь граней пластины; V = (Sd) - ее объем) и далее
(S - площадь граней пластины; V = (Sd) - ее объем) и далее
 (3.6)
(3.6)
то есть поверхностная плотность связанных зарядов равна поляризованности диэлектрика. Тогда в соответствии с (3.6) и (3.3) выражение (3.5) принимает вид:
Е = Е0 -хЕ, (3.7)
откуда напряженность результирующего поля внутри диэлектрика равна

где диэлектрическая проницаемость
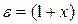 . (3.9)
. (3.9)
Таким образом, эмпирически введенная Кулоном в (1.1) безразмерная величина  (диэлектрическая проницаемость среды), показывающая во сколько раз электростатическое поле ослабляется диэлектриком, характеризует также количественно свойство диэлектрика поляризовываться в электростатическом поле. Напряженность электростатического поля согласно (3.8) зависит от свойств среды и вектор
(диэлектрическая проницаемость среды), показывающая во сколько раз электростатическое поле ослабляется диэлектриком, характеризует также количественно свойство диэлектрика поляризовываться в электростатическом поле. Напряженность электростатического поля согласно (3.8) зависит от свойств среды и вектор  , переходя через границу диэлектриков, скачкообразно меняется по величине (скачкообразно меняется густота линии
, переходя через границу диэлектриков, скачкообразно меняется по величине (скачкообразно меняется густота линии  на границе раздела сред и направлению). Это обстоятельство затрудняет расчет электростатических полей. Поэтому помимо вектора
на границе раздела сред и направлению). Это обстоятельство затрудняет расчет электростатических полей. Поэтому помимо вектора 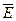 электростатические поля характеризуют и второй силовой характеристикой - вектором электрического смещения
электростатические поля характеризуют и второй силовой характеристикой - вектором электрического смещения  (индукция электрического поля), который для изотропной среды по определению равен
(индукция электрического поля), который для изотропной среды по определению равен
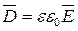 , (3.10)
, (3.10)
а используя (3.3) и (3.9), его можно выразить, как
 . (3.11)
. (3.11)
Аналогично, как и поле вектора 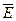 , поле вектора
, поле вектора  изображается с помощью линий вектора электростатического смещения, направление и густота, которых определяются точно так же, как и для линий напряженности. Линии вектора
изображается с помощью линий вектора электростатического смещения, направление и густота, которых определяются точно так же, как и для линий напряженности. Линии вектора 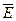 могут начинаться и заканчиваться на любых зарядов (свободных и связанных), а линии
могут начинаться и заканчиваться на любых зарядов (свободных и связанных), а линии  - только на свободных зарядах. С учетом этого и согласно (3.11) можно сделать вывод, что вектор
- только на свободных зарядах. С учетом этого и согласно (3.11) можно сделать вывод, что вектор  не зависит от свойств среды, то есть линии вектора
не зависит от свойств среды, то есть линии вектора  проходят границы диэлектриков не прерываясь.
проходят границы диэлектриков не прерываясь.
Для вектора  (так же как и для
(так же как и для 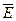 ) справедлива теорема Гаусса, которая для электростатического поля в диэлектрике имеет вид
) справедлива теорема Гаусса, которая для электростатического поля в диэлектрике имеет вид
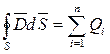 , (3.12)
, (3.12)
то есть поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных зарядов (и в дифференциальной форме  ).
).
Связанные заряды появляются в диэлектрике при наличии внешнего электрического поля, создаваемого системой свободных зарядов. Вектор напряженности 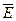 как раз и описывает результирующее поле свободных и связанных зарядов в диэлектрике (поэтому он и зависит от свойств среды). Вектором
как раз и описывает результирующее поле свободных и связанных зарядов в диэлектрике (поэтому он и зависит от свойств среды). Вектором  описывается электростатическое поле свободных зарядов. Но, как правило, связанные заряды, возникающие в диэлектрике, вызывают перераспределение свободных зарядов, создающих внешнее поле. Поэтому вектор
описывается электростатическое поле свободных зарядов. Но, как правило, связанные заряды, возникающие в диэлектрике, вызывают перераспределение свободных зарядов, создающих внешнее поле. Поэтому вектор  характеризует электростатическое поле, создаваемое свободными зарядами (то есть в вакууме), но при таком их распределении в пространстве, которое установится при наличии диэлектрика.
характеризует электростатическое поле, создаваемое свободными зарядами (то есть в вакууме), но при таком их распределении в пространстве, которое установится при наличии диэлектрика.