Для уединенного проводника (удаленного от других тел и зарядов) применимо выражение (2.7) для потенциала поля точечного заряда, из которого следует, что потенциал такого проводника прямо пропорционален его заряду (что подтверждается экспериментом). Коэффициент пропорциональности " С ": 
или
(3.19)
- называют электроемкостью (или просто емкостью) уединенного проводника. Согласно (3.19) емкость уединенного проводника определяется зарядом, сообщение которого проводнику повышает его потенциал на единицу. В СИ единица емкости: 
. Емкость проводника зависит от его размеров, формы и среды, в которой он находится. Емкость не зависит ни от заряда, ни от потенциала проводника. Это не противоречит (3.19), так как оно лишь показывает, что для данного проводника отношение заряда к потенциалу есть величина постоянная.
Используя (3.19) и (2.7) для проводящего шара, находящегося в среде с диэлектрической проницаемостью 
, можно получить, что его емкость равна
. (3.19а).
Численная оценка дает, что уединенный шар емкостью 1 Ф в вакууме должен иметь радиус R ≈ 9·106 км ≈ 1400 Rземли. Эти цифры свидетельствуют о том, что 1 Ф - очень большая емкость. Поэтому на практике используют производные единицы: миллифарад (мФ = 10-3 Ф), микрофарад (мкФ = 10-6 Ф); нанофарад (нФ = 10-9 Ф); пикофарад (пФ = 10-12 Ф). Из рассмотренного следует, что для уединенных проводников большие емкости связаны с их большими размерами.
На практике требуются устройства, способные при малых размерах накапливать значительные заряды, то есть обладать большой емкостью. Такие устройства называют конденсаторами.
Если к заряженному уединенному проводнику приближать другие тела, то на них возникают индуцированные (смещенные) на проводнике или связанные (на диэлектрике) заряды противоположного знака. Эти заряды ослабляют поле уединенного проводника, то есть понижают его потенциал, что приводит согласно (3.19) к повышению емкости. Так (в упрощенном варианте) выглядит идея конструкции любого конденсатора. Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. Чтобы на емкость конденсатора не оказывали влияние окружающие тела, проводникам придают такую форму, чтобы поле, создаваемое накапливаемым зарядом, было сосредоточено в узком зазоре между обкладками конденсатора.
Наиболее распространены в технике конденсаторы, состоящие из двух параллельных металлических пластин площадью " S " - каждая, расположенных на расстоянии " d " друг от друга и несущих заряды "+ Q " и "- Q ". Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь, и поле между обкладками считать однородным.
Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (
) между его обкладками
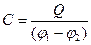. (3.19б)
Если пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью , то в соответствии с (3.8) получим
. (3.20)
С учетом того, что 
, из (3.19б) приходим к выражению для емкости плоского конденсатора
. (3.21)
Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи, используя их параллельное и последовательное соединения (рис. 3.4).
У параллельно соединенных конденсаторов (рис. 3.4а) разность потенциалов на обкладках одинакова и равна (
). Если емкости отдельных конденсаторов C1; C2; … Cn, то из (3.20) следует, что их заряды равны: 
; 
;… 
, а заряд батареи конденсаторов
.
Полная емкость батареи
, (3.22)
то есть при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов.
У последовательно соединенных конденсаторов (рис. 3.4б) заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи 
, где для любого из рассматриваемых конденсаторов 
.
Рис.3.4
С другой стороны 
, откуда
, (3.23)
то есть при последовательном соединении конденсаторов в батареи суммируются величины обратные емкостям.