Указания к построению кодов

МЕТОДЫКОДИРОВАНИЯ ИНФОРМАЦИИ В КАНАЛАХ СВЯЗИ

ЛАБОРАТОРНЫЕ РАБОТА №2

 

ПОСТРОЕНИЕ И РЕАЛИЗАЦИЯ ЭФФЕКТИВНЫХ КОДОВ

 

Целью работы является усвоение принципов построения и технической реа­лиза­ции кодирующих и декодирующих устройств эффективных кодов.

 

Указания к построению кодов

Учитывая статистические свойства источника сообщений, можно миними­зиро­вать среднее число двоичных символов, требующихся для выражения од­ной буквы сообщений, что при отсутствии шума позволяет уменьшить время передачи или емкость запоминающего устройства. Такое эффективное кодиро­вание базируется на основной теореме Шеннона для каналов без шума.

К. Шеннон доказал, что сообщения, составленные из букв некоторого алфа­вита, можно закодировать так, что среднее число двоичных символов на бу­кву будет сколь угодно близко к энтропии источника этих сообщений, но не менее этой вели­чины.

Теорема не указывает конкретного способа кодирования, но из нее сле­дует, что при выборе каждого символа кодовой комбинации необходимо ста­раться, чтобы он нес максимальную информацию. Следовательно, каждый сим­вол должен принимать значения 0 или 1 по возможности с равными вероятно­стями, и каждый выбор должен быть независим от значений предыдущих сим­волов.

Для случая отсутствия статистической взаимосвязи между буквами кон­струк­тивные методы построения эффективных кодов были даны впервые Шен­ноном и Фено. Их методики существенно не отличаются, и поэтому соответст­вующий код по­лучил название кода Шеннона - Фено.

Код строится следующим образом: буквы алфавита сообщений выписыва­ются в таблицу в порядке убывания вероятностей их встречаемости. Затем их разделяют на две группы так, чтобы суммы вероятностей встречаемости букв в каждой из групп были бы по воз­можности одинаковыми. Всем буквам верхней половины в качестве первого сим­вола записывается ­– 1, а всем нижним – 0. Каждая из полученных групп, в свою очередь, разбивается на две под­группы с одинаковыми суммарными веро­ятностями и т.д. Процесс повторяется до тех пор, пока в каждой подгруппе не останется по одной букве.

Все буквы будут закодированы различными последовательностями символов из “0” и ”1” так, что ни одна более длинная кодовая комбинация не будет начинаться с более короткой, соответствующей другой букве. Код, обладающий этим свойством, называется индексным. Это позволяет вести запись текста без разделительных символов и обеспечивает однозначность декодирования.

Рассмотрим алфавит из 8 букв. Ясно, что при обычном (не учитывающем вероятностей встречаемости их в сообщениях) кодировании для представления каждой бу­квы требу­ется 3 символа (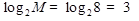), где M – количество букв в алфавите.

Наибольший эффект "сжатия" получается в случае, когда вероятности встречаемости букв представляют собой целочисленные отрицательные степени двойки. Среднее число символов на букву в этом случае точно равно энтропии. В более общем слу­чае для алфавита из 8 букв среднее число символов на букву будет меньше трех, но больше энтропии алфавита H(M).

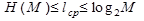
Для алфавита, приведенного в табл.1.1, энтропия H(M) равна 2.76, а среднее число символов на букву:

,

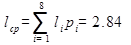где l_i – количество символов для обозначения i -ой буквы.

 

Таблица 1.1

Буква	Вероятности	Кодовая ком­бинация	№ деления
A1 A2 A3 A4 A5 A6 A7 A8	0.22 0.20 0.16 0.16 0.10 0.10 0.04 0.02		II III I IV V VI VII

 

Следовательно, некоторая избыточность в кодировании букв осталась. Из теоремы Шеннона следует, что эту избыточность можно устранить, если перейти к кодированию блоками.

Рассмотрим сообщения, образованные с помощью алфавита, состоящего всего из двух букв А₁ и А₂ с вероятностями появления соответственно

Р₁ (А₁)=0,9и Р₂ (А₂)=0,1.

Поскольку вероятности не равны, то последовательность из таких букв бу­дет обладать избыточностью. Однако, при побуквенном кодировании мы ни­какого эффекта не получим.

Действительно, на передачу каждой буквы требуется символ либо 1, либо 0, в то время как энтропия равна 0,47. При кодировании блоками, вклю­чающими по две буквы, получим табл. 1.2. Так как буквы статистически не свя­заны, вероятности встречаемости бло­ков определяют как произведение вероятностей состав­ляющих их букв.

Таблица 1.2

Буква	Вероятности	Кодовая ком­би­нация	№ деления
А1А1 А1А2 А2А1 А2А2	0.81 0.09 0.09 0.01		I II III

Среднее число символов на блок получается равным 1.29, а на букву – 0.645.

Кодирование блоков, включающих по три буквы, дает еще больший эф­фект. Среднее число символов на блок в этом cлучае равно 1,59, а на букву – 0,53, что всего на 12% больше энтропии. Теоретический минимум Н(M)= 0,47 может быть достигнут при кодировании блоков, включающих бесконечное число букв:

 

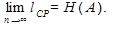
Следует подчеркнуть, что уменьшение l_ср при увеличении числа букв в блоке не связано с учетом статистических связей между соседними буквами, так как нами рассматривались алфавиты с некоррелированными буквами. По­вышение эффективности определяется лишь тем, что набор вероятностей, по­лучающийся при укрупнении блоков, можно делить на более близкие по сум­марным вероятностям подгруппы.

Для учета взаимосвязи между буквами текста, кодирование очередной буквы необходимо вести с учетом предыдущей последовательности букв в зависимости от глубины этой связи. При таком кодировании энтропия на одну букву уменьшается, но существенно усложняется система кодирования, поскольку приходится учитывать не один столбец вероятностей, а M^m столбцов, где m – глубина взаимосвязи между соседними буквами.

Рассмотренная нами методика Шеннона - Фано не всегда приводит к одно­значному построению кода, так как, разбивая на подгруппы, большей по сум­марной вероятности можно сделать как верхнюю, так и нижнюю подгруппы.

Вероятности, приведенные в табл.1.1, можно было бы разбить иначе (табл. 1.3):

Таблица 1.3

Буква	Вероятности	Кодовая ком­бинация	№ разбиения
A1 A2 A3 A4 A5 A6 A7 A8	0.22 0.20 0.16 0.16 0.10 0.10 0.04 0.02		II I IV III V VI VII

 

При этом среднее число символов на букву оказывается равным 2.80. Таким образом, построенный код может оказаться не самым лучшим. При по­строении эф­фективных кодов с основанием m>2 неопределенность становится еще больше. От указанного недостатка свободна методика Хаффмена. Она га­рантирует однозначное построение кода с наименьшим для данного распреде­ления вероятностей средним числом символов на букву. Для двоичного кода методика сводится к следующему.

Буквы алфавита сообщений выписываются в первый столбец в порядке убывания вероятностей. Две последние вероятности объединяются в одну вспомога­тельную, которой приписывается суммарная вероятность. Вероятности букв, не участ­вующих в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние вероятности снова объе­диняются. Процесс продолжается до тех пор, пока не получим единственную вспо­могательную вероятность равную единице. Поясним методику на примере (табл. 1.4). Значения вероятностей примем те же, что и в табл. 1.1.

Для получения кодовой комбинации, соответствующей данной букве, необходимо проследить путь перехода ее вероятности по строкам и столбцам табл. 1.4. Для наглядности построим кодовое дерево. Из точки, соответствую­щей вероятно­сти 1, направим две ветви, причем ветви с большей вероят­ностью присвоим символ 1, а с меньшей – 0. Такое последовательное ветвление продолжим до тех пор, пока не дойдем до вероятности каждой буквы. Кодовое дерево для алфа­вита букв, рассматриваемого в нашем примере, приведено на рис. 1.1.

Таблица 1.4

Буква	Вероятности	Вспомогательные столбцы
A1 A2 A3 A4 A5 A6 A7 A8	0.22 0.20 0.16 0.16 0.10 0.10 0.04 0.02
0.22 0.20 0.16 0.16 0.10 0.10 0.06	0.22 0.20 0.16 0.16 0.16 0.10	0.26 0.22 0.20 0.16 0.16	0.32 0.26 0.22 0.20	0.42 0.32 0.26	0.58 0.42	1

 

Теперь, двигаясь по кодовому дереву от единицы через промежуточные вероятности к вероятностям каждой буквы, можно записать соответствующую ей кодовую комбинацию: А₁ - 01, А₂ - 00, А₃ - 111, А₄ - 110, А₅ - 100, А₆-1011, А₇ - 10101, А₈ - 10100. При этом получим l_ср =2,80 символа на букву.

 

 

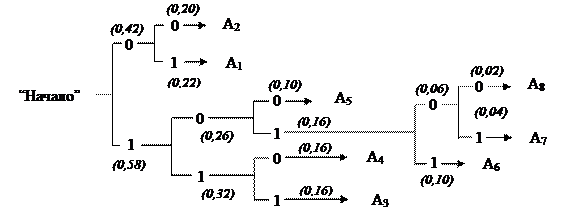Рис. 1.1. Кодовое дерево

 

 

ЗАДАНИЕ

1. Изучить описание, изучить методы построения и технической реализации эффективных кодов.

2. По конкретным значениям вероятностей встречаемости букв в сообщении, которое было исследовано в лабораторной работе №1, построить эффективный код, используя методики Шеннона-Фано и Хаф­фмана.

Вычислить энтропию источника и среднюю длину комбинации полученного кода.

5. Зарисовать таблицу и дерево Хаффмана.

6. Подсчитать выигрыш от записи текста эффективным кодом.

Требования к отчету

 

Отчет должен включать:

1. таблицу построения эффективного кода по методике Шеннона-Фено;

2. таблицу и кодовое дерево, иллюстрирующие построение эффективного кода по методике Хаффмена.

3. Результаты расчетов энтропии источника и среднюю длину кода для буквы, отдельно для заданного Вами алфавита и текста.