Выбор образующего многочлена

Лабораторная работа №4

ПОСТРОЕНИЕ И РЕАЛИЗАЦИЯ ЦИКЛИЧЕСКИХ КОДОВ

Целью работы является усвоение методов построения и технической реа­лизации кодирующих и декодирующих устройств циклических кодов.

1. Указания к построению кодов.

Математической основой циклических кодов является теория колец. В качестве основных операций в циклическом коде используются операции сложения по модулю два и символического умножения, в котором для сохранения степени многочлена не выше (n-1) используется искусственный прием. Если степень многочлена после умножения не выше n-1, то он и принимается за результат умножения, а если выше, то он делится на другой многочлен (xⁿ+1) и в качестве результата умножения принимается остаток от деления.

Выбор образующего многочлена

Любой групповой (n,k) код может быть записан в виде матрицы, вклю­чающей k линейно-независимых строк по n символов. Среди всего многообразия таких кодов можно выделить коды, у которых строки обра­зующих матриц связаны дополнительным условием цикличности.

Все строки образующей матрицы такого кода могут быть получены цикли­ческим сдвигом одной комбинации: называемой образующей для данного кода. Коды, удовлетворяющие этому условию, получили название циклических ко­дов.

Сдвиг осуществляется справа налево, причем крайний левый символ каж­дый раз переносится в конец комбинации. Запишем, например, образующую матрицу кода, получающуюся циклическим сдвигом комбинации 001011:

	G =

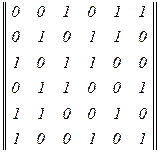При описании циклических кодов n -разрядные кодовые комбинации пред­ставляются в виде многочленов фиктивной переменной х. Показатели степени у х соответствуют номерам разрядов (начиная с нулевого), а коэффициентами при х являются цифры 0 и 1 (поскольку мы рассматриваем двоичные коды).

Запишем, например, в виде многочлена образующую кодовую комбина­цию 001011

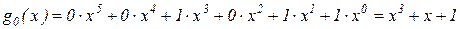
Действия над кодовыми комбинациями теперь сводятся к действию над многочленами.

Вышеупомянутый циклический сдвиг образующего многочлена без пере­носа единицы в конец кодовой комбинации соответствует простому умноже­нию на х. Например, вторая строка матрицы есть

g₀ (x)x=x⁴+x²+x (010110).

Циклический сдвиг строки матрицы с единицей в старшем разряде (слева) равносилен умножению соответствующего многочлена на х с одновре­менным вычитанием из результата многочлена х^п+1

Поскольку операции вычитания и сложения по модулю два тождественны, многочлен, соответствующий любой строке матрицы, может быть записан в виде

g_i(x)=g₀(x)xⁱ+С(xⁿ+1),

где С равно 1, если степень g₀(x)xⁱ превышает n-1, и нулю, если не превы­шает.

Если выбрать за образующий такой многочлен g₀(x), который является де­лителем двучлена xⁿ+1, то все многочлены матрицы, а поэтому и все много­члены кода (разрешенные кодовые комбинации), будут делиться на g₀ (x) без остатка. Ни один многочлен, соответствующий запрещенной кодовой комбина­ции, на образующий многочлен нацело не делится. Это свойство позволяет об­наруживать ошибки. По виду остатка можно определить и вектор ошибки, а, следовательно, и устранить ее.

Любая принятая кодовая комбинация h(x), содержащая ошибку, может быть представлена в виде суммы по модулю два неискаженной комби­нации кода f(x), делящейся на g₀(x) без остатка, и вектора ошибки e(x). Для од­нозначности декодирования каждому вектору ошибки должен соответствовать отличный от других остаток - опознаватель. Чем больше различных остатков может быть образовано при делении h(x) на g₀(x), тем больше разновидностей ошибок способен исправить данный циклический код.

Наибольшее число остатков, равное 2^m-1 (исключая нулевой), может обес­печить только неприводимый (простой) многочлен g₀(x) степени m, принадле­жащий показателю степени п, если m и n связаны соотношением n= 2^m-1.

В литературе по кодированию доказано, что для любого т существует по крайней мере один неприво­димый многочлен степени т, принадлежащий показателю степени п, если n=2^m-1.

При известном числе информационных символов (к) задача, следова­тельно, сводится к тому, чтобы определить наименьшую степень т образую­щего многочлена, обеспечивающего обнаружение или исправление ошибок за­данной кратности. Зная п и т по имеющимся в ряде книг таблицам много­членов, неприводимых при двоичных коэффициентах, можно выбрать и кон­кретный образующий многочлен.

Для исправления одиночных ошибок требуемая минимальная степень образующего многочлена (m) на­ходится из соотношения

2^т-1=2^п-k-1³ C¹_n

Выберем, например образующий многочлен для случая к =4. Тогда п =7 и т =3.

В таблице неприводимых многочленов, принадлежащих степени п, нахо­дим два многочлена третей степени, так как х⁷+1=(х+1)(х³+х+1)(х³+х²+1).

Примем за образующий многочлен g(x)=x³+x²+1 (1101). Чтобы убедится, что каждому вектору ошибки соответствует отличный от других остаток, поде­лим каждый из этих векторов на g₀(x).

Векторы ошибок т младших разрядов имеют вид:

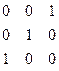
Степени соответствующих им многочленов меньше степени образующего многочлена g₀(x). Поэтому они сами являются остатками при нулевой целой части. Остаток, соответствующий ошибке в следующем разряде, получается при делении 1000 на 1101, т.е.

1000 1101

1101

Аналогично могут быть найдены и остальные остатки. Однако их можно получить проще, деля на g₀(x) комбинацию в виде единицы с рядом нулей и выписывая все промежуточные остатки

1000000000 1101 Остатки

1101

1010 101

1101 111

1110 011

1101 110

01100 001

1101 010

001000 100

При последующем делении остатки повторяются.

Если выбрать в качестве образующего многочлена 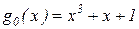, то тоже получим требуемое число различных остатков – 7.

Если k =5 и требуется исправлять тоже одиночную ошибку, то 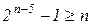. Откуда получаем n_min =9 и m= n – k =9–5=4. Примем 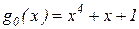. Этот образующий многочлен сохранится до k =11, так как неравенство 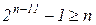будет выполняться при n_min =15 и m =4.