ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения первого порядка.
Основные понятия
Дифференциальным уравнением (ДУ) называется уравнение, связывающее независимую переменную 
, искомую функцию 
и её производные или дифференциалы.
- 
- дифференциальное уравнение первого порядка, неявный вид.
- 
- уравнение, разрешённое относительно производной.
- 
- дифференциальная форма записи дифференциального уравнения первого порядка.
ДУ с одной независимой переменной называется обыкновенным.
Порядком ДУ называется порядок наивысшей производной (или дифференциала), входящей в уравнение.
Всякая функция, удовлетворяющая ДУ, т.е. при подстановке в уравнение обращающая его в тождество, называется решением уравнения. Бесконечное множество решений уравнения называется общим решением ДУ. Общее решение имеет вид 
, где C – произвольная постоянная. Если решение задано в неявном виде, то оно обычно называется интегралом. Множество интегралов называется общим интегралом и имеет вид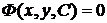 
.
Каждому решению уравнения соответствует линия (график), называемая интегральной кривой этого уравнения.
Задача отыскания решения ДУ первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши.
Теорема (существования и единственности задачи Коши). Если функция 
непрерывна в области, содержащей точку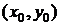 
, то уравнение имеет решение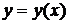 
такое, что 
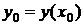. Если, кроме того, непрерывна и частная производная 
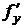, то это решение – единственное.
Условие, при котором значение искомой функции равно 
при 
, называется начальным условием уравнения и записывается 
.
Решение ДУ, удовлетворяющее заданному начальному условию, называется частным решением.
Например.
а)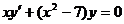 
– ДУ 1-го порядка в неявном виде.
б) 
– ДУ 1-го порядка в дифференциальной форме.
в) 
– ДУ 1-го порядка разрешенное относительно производной.
Пример 1. Выяснить, является ли функция 
решением уравнения 
?
Решение.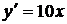 
. Полученную производную подставим в уравнение. Тогда 
, 
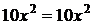. Получили верное тождество, следовательно, данная функция является решением данного ДУ.
Дифференциальные уравнения первого порядка
и методы их решения. Метод изоклин (графическое решение)
Геометрическое истолкование ДУ первого порядка. Уравнение устанавливающее связь (зависимость) между координатами точки 
и угловым коэффициентом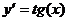 
касательной интегральной кривой, проходящей через эту точку. Следовательно, ДУ дает совокупность направлений (поле направлений) на плоскости Оху.
Поле направлений изображаетсяпри помощисистемы чёрточек или стрелок с углом наклона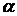 
.
Кривые 
(где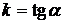 
), в точках которых наклон поля имеет постоянное значение, равное k, называются изоклинами. Построив изоклины и поле направлений, можно приближённо нарисовать интегральные кривые, рассматривая последние как кривые, которые в каждой своей точке имеют заданное направление поля.
Пример 2. Методом изоклин построить приближенно поле интегральных кривых для дифференциальног уравнения 
.
Решение. Здесь изоклинами являются прямые линии:
, где 
, 
, 
;
, 
, 
;
, 
, 
.
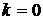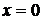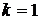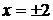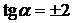
На каждой из прямой изображаем систему черточек под найденным углом. Проводя линии таким образом, чтобы черточки являлись касательными к интегральным кривым, получим параболы (рис. 12)
Рисунок 12