ДУ вида 
называются уравнениями с разделенными переменными. Решаются такие ДУ путем непосредственного интегрирования обеих частей равенства по соответствующим переменным.
Пример 3. Найти общее решение ДУ 
.
Решение. , 
, 
, 
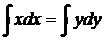– общий интеграл (общее решение).
ДУ вида 
называются уравнениями с разделяющимися переменными.
Для решения дифференциального уравнения данного вида необходимо перенести одно слагаемое в правую сторону: 
и разделить обе части на 
, получим дифференциальное уравнение с разделенными переменными 
.
Пример 4. Решить ДУ 
.
Решение. 
. Делим обе части уравнения на
. (
.
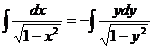
Однородные дифференциальные уравнения
Если ДУ 1-го порядка можно записать в виде 
с помощью алгебраических преобразований, то это уравнение называется однородным дифференциальным уравнением.
Например, уравнение 
– однородное, так как 
.
Решают однородное уравнение заменой: 
или 
, тогда 
(если уравнение задано в дифференциалах, то 
).
Пример 5. Решить дифференциальное уравнение 
.
Решение. Преобразуем данное уравнение к виду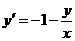 
.
Сделаем замену , . Получаем уравнение 
. В результате преобразований его можно привести к виду 
. Таким образом, имеем ДУ 1-го порядка с разделенными переменными. Решая его, получим: 
. Так как , то 
. Получаем 
– общее решение данного ДУ.
Приводящееся дифференциальное уравнение
Пусть 
тогда:
- если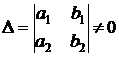 
, то полагают 
Здесь 
и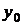 
– const, определяемые из системы уравнений 
Так как 
то получим однородное дифференциальное уравнение относительно переменных 
и 
.
- если 
, то, полагая в уравнении 
, получим уравнение с разделяющимися переменными.
Пример 6. Решить уравнение 
.
Решение. 
, делаем замену 
, тогда 
.
Тогда 
– уравнение с разделяющимися переменными. Решая его, получим 
. Вернемся к переменным 
и 
:
.
Линейные уравнения первого порядка
Дифференциальное уравнение вида 
, где 
и 
– заданные функции (в частности, постоянные), называется линейным.
Рассмотрим два метода решения линейного ДУ – метод Лагранжа и метод Бернулли.
Метод Лагранжа (метод вариации произвольной постоянной)
В общем случае, если 
, то уравнение называется линейным неоднородным ДУ (ЛНДУ) первого порядка. Рассмотрим соответствующее уравнение без правой части, т. е. уравнение 
. Оно называется линейным однородным ДУ (ЛОДУ) первого порядка. В этом уравнении переменные делятся: 
.
Метод вариации произвольной постоянной состоит в том, что постоянную С в полученном решении заменяют на функцию С (х). Тогда решение ЛНДУ находится в виде 
.
Находим производную: 
.
Подставляем у и 
в ЛНДУ:
,
.
Учитывая, что 
, запишем 
.
Интегрируя, находим 
.
Таким образом, получим общее решение ЛНДУ в виде
.
Пример 7. Решить ДУ 
.
Решение. Данное уравнение является линейным уравнением первого порядка. Здесь 
, 
. Решаем сначала однородное уравнение 
. Имеем 
или 
. Заменяем С на С (х), т. е. решение линейного уравнения ищем в виде 
. Тогда 
. Подставляя выражения для у и в уравнение, получим 
или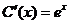 
. Отсюда находим С (х):
. Следовательно, 
– искомое решение.
.
Метод Бернулли
Запишем функцию в виде произведения двух функций 
. Находим производную 
. Подставим все в данное уравнение 
или 
выражение в квадратных скобках приравняем к нулю. Отсюда 
, тогда для отыскания получим уравнение 
.
Сначала найдем из уравнения 
– ДУ с разделяющимися переменными: 
, 
, 
, придадим с любое значение, пусть 
, тогда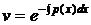 
.
Зная , найдем из уравнения : 
– уравнение с разделяющимися переменными, отсюда 
.
Найдем искомую функцию : 
– эта формула дает общее решение линейного уравнения.
Замечание. Формулу запоминать не имеет смысла, необходимо помнить алгоритм решения.
Пример 8. Решить уравнение .
Решение. Положим ; тогда . Имеем:
, 
. (1)
, тогда 
.
Значит 
. Пусть 
, тогда 
.
Для нахождения функции вернемся к уравнению (1): 
, 
, 
, 
.
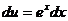Зная, и окончательно имеем: 
.
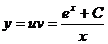Уравнение Бернулли
Уравнение вида 
, где 
и 
, называется уравнением Бернулли. Данное уравнение также решают методами Лагранжа или Бернулли.
Решите самостоятельно ДУ 
любым из указанных методов.