По закону Био-Савара-Лапласа индукция магнитного поля пропорциональна току, текущему в контуре, то есть В~ J. Магнитный поток пропорционален магнитной индукции, а значит и току в контуре:
, (8.2)
где коэффициент пропорциональности L называется индуктивностью контура. Тогда 
и при J =1, L = Ф, то есть индуктивность контура определяется величиной магнитного потока, сцеплённого с контуром, в котором течёт единичный ток. Единица индуктивность в СИ – 1 Генри [1Гн = 1Вб/1А].
Индуктивность контура зависит от геометрической формы контура, его размеров и магнитных свойств среды, в которой он находится. В этом смысле индуктивность контура – аналог электроёмкости уединённого проводника.
Проиллюстрируем это на примере соленоида. Полный магнитный поток через соленоид:
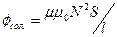. (8.3)
Если текущий в контуре ток изменяется, будет меняться и сцеплённый с ним магнитный ток, а значит в контуре будет индуцироваться ЭДС, которая в этом случае называется ЭДС самоиндукции 
, а явление её возникновения называют самоиндукцией. Применяя к этому явлению закон Фарадея (8.1) и учитывая, что в большинстве реальных ситуаций контур не деформируется и магнитная проницаемость среды не меняется, получим выражение для ЭДС самоиндукции (при условии L =const):
. (8.4)
Отсюда при 
, 
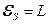и индуктивность L контура численно равна индуцированной в нём ЭДС самоиндукции при условии равенства скорости изменения тока в нём единице. Размерность 
1Гн = 1 В/(А·с) = 1 Вб/А.
Выражение (8.4) хорошо иллюстрирует гибкость и вариативность проявления действия правила Ленца. Так при возрастании тока в контуре 
>0. Согласно (8.4) 
<0, то есть ток самоиндукции направлен навстречу току, обусловленному внешним источником и тормозит его возрастание. В обратной ситуации при убывании тока в контуре (то есть <0) согласно (8.4) >0, то есть индуцированный ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, обладая определённой индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любые изменения тока тормозятся тем сильнее, чем больше индуктивность контура. Можно сказать, что роль индуктивности в электрических цепях аналогична роли массы в механике, то есть индуктивность является мерой электрической инертности.
В качестве примера рассмотрим выключение тока в цепи, содержащей источник тока с ЭДС 
, резистор сопротивлением R и катушку индуктивностью L. Под действием внешний ЭДС в цепи течёт постоянный ток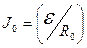 
(считается, что внутренним сопротивлением источника можно пренебречь). При t = 0 происходит отключение источника тока, ток начинает уменьшаться и появляется ЭДС самоиндукции 
. Мгновенное значение тока (по закону Ома) 
или 
. Разделив переменные и проинтегрировав правую и левую часть этого уравнения по 
и по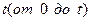 
получим 
или
. (8.5)
Таким образом, при отключении ЭДС сила тока в цепи убывает по экспоненциальному закону (8.5). Чем больше индуктивность цепи и меньше её сопротивление, тем медленнее уменьшается ток в цепи при её размыкании. Оценим значение ЭДС самоиндукции , возникающей при размыкании цепи постоянного тока, то есть при мгновенном увеличении сопротивления цепи от R0 до 
. Если цепь разомкнуть при установившемся токе 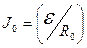, то далее ток изменяется в соответствии с (8.5) 
и при этом текущая ЭДС самоиндукции равна
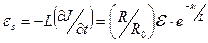. (8.6)
Таким образом, при размыкании цепи и значительном увеличении сопротивления цепи 
, обладающей большой индуктивностью, ЭДС самоиндукции во много раз (из 8.6 получаем 
), превышает ЭДС источника тока, включенного в цепь. Отсюда вытекает, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (благодаря возникновению значительной ЭДС самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контуре сопротивление выводить постепенно, (используя мощные «пусковые» реостаты), то ЭДС самоиндукции не достигнет больших значений. Аналогичное мероприятие необходимо осуществлять и при замыкании цепи постоянного тока.