Пример 1. Произвести 0-1 нормализацию 
вида: 
.
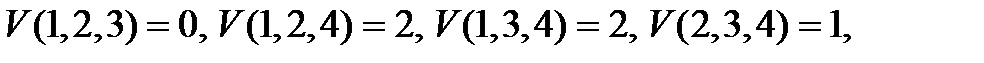
Решение.
Нормализация производится для существенных игр, т.е. 
. Проверим, является ли игра существенной: 
или 
- игра существенная. Нормализация характеристической функции производится по формуле
Для рассматриваемой игры 
. Определим 
на 
и 
(по определению, 
):
а) для имеем: 
, 
б) для имеем: 
Получили 
вида
Пример 2. Для 
из примера 1 привести примеры дележей.
Решение.
По определению, вектор 
является дележом в условиях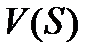 
, если для него выполняются условия индивидуальной и коллективной рациональности:
Для 0-1 нормализации 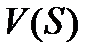- имеем: 
тогда 
. Действуя в соответствии с этими соотношениями, получим следующие дележи: пусть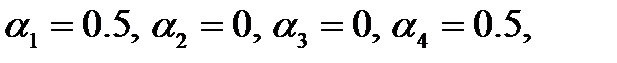 
тогда имеем дележ с компонентами: 
; пусть 
тогда компоненты дележа и дележ равны: 
. Отметим, что дележей – бесконечное множество.
Пример 3. Для примера 1 привести примеры дележей 
и 
таких, что доминирует на коалиции 
- 
.
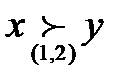Решение.
Дележ 
доминирует дележ 
на коалиции (по коалиции) 
, если выполняются условия:
а) 
- условие доминирования компонент;
б) 
- условие реализуемости дележа.
Пусть 
проверим условия доминирования на 
:
а) 
или 
- условия выполняются;
б) 
или 
- не выполняется, т.е. дележ нереализуем.
Пусть 
проверим условие доминирования:
а) 
или 
- выполняются;
б) 
или 
- выполняется, значит дележ доминирует дележ на 
в условиях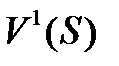 
примера 1.
Пример 4. Показать, какой из двух дележей 
, 
предпочтительней другого, если условия реализуемости дележей выполняются.
Решение.
Возможные варианты доминирований: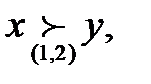 
. Условия покомпонентного доминирования выполняется для 
для дележа 
:
, т.к. 
или 
Для остальных коалиций ни один из вариантов доминирования не выполняется. Геометрическая интерпретация решения приводится на рис. 12, рис. 13.
Рис. 12. Множества дележей, доминируемых дележом 
Рис. 13. Множества дележей, доминируемых дележом 
Пример 5. Игра «джаз-оркестр». Постановка задачи. Оркестр из трех человек: певец, пианист, ударник, за совместную игру в клубе может получить 1000 ден.ед.; за выступление певца с пианистом – 800 ден.ед.; за выступление ударника и пианиста – 650 ден. ед.; за выступление пианиста (соло) – 300 ден.ед. Другие дуэты не рассматриваются, т.к. присутствие пианиста обязательно. Кроме того, работая в кафе, певец и ударник могут заработать 500 ден.ед., а один певец – 200 ден.ед.; один ударник не зарабатывает ничего.
Найти справедливое распределение максимального выигрыша, с учетом приведенных возможностей оценки индивидуальной и коллективной работы.
Решение.
Имеем 
трех лиц: 
- певец, 
- пианист, 
- ударник. Примем в качестве критерия оптимальности дележей устройчивость в смысле С-ядра. По определению, дележ принадлежит С-ядру, если выполняются условия
(2.13)
Прежде чем записать условия (2.13),формализуем характеристическую функцию игры:
(2.14)
Произведем 0-1 нормализацию 
, по формуле
1) 
- по определению;
2) 
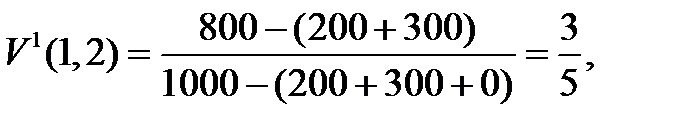
Получили 0-1 нормализацию
(2.15)
Из (2.15) имеем: 
. Проверим необходимые условия существования непустого С-ядра
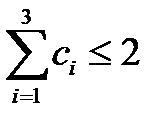или 
, значит 
.
Запишем условия (2.13) и, используя условие коллективной рациональности, запишем ограничения на выигрыши игроков:
или 
или 
(2.16)
Дадим геометрическую интерпретацию С-ядра (рис. 14).
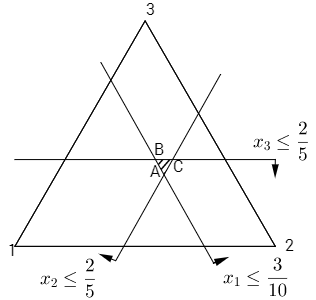
Рис. 14. С-ядро игры «джаз-оркестр»
В соответствии с рис. 14, любая точка заштрихованного треугольника является дележом игры. В качестве примеров дележей возьмем точки,
соответствующие вершинам 
:
1) вершина А: 
, тогда имеем дележ 
2) вершина B: 
тогда имеем дележ 
3) вершина С: 
тогда имеем дележ 
.
Пример 6. Показать, что для 
с постоянной суммой решение по Нейману-Моргенштерну состоит из трех дележей:
Решение.
По определению, множество дележей, составляющих решение по Нейману-Моргенштерну, обладает свойствами внутренней и внешней устойчивости; проверим эти свойства.
1. Внутренняя устойчивость – никакие два дележа не доминируют друг друга. Рассмотрим все возможные доминирования дележей: 
и наоборот - 
на коалициях 
. По определению, дележ 
доминирует дележ 
на коалиции 
если:
а) 
б) 
Условие а) не выполняется ни для одного дележа, значит доминирования на коалиции нет. Аналогично проверяются доминирования на коалициях 
.
2. Внешняя устойчивость – множество дележей 
обладает внешней устойчивостью, если любой дележ 
, не принадлежащий множеству 
, доминируется дележом из 
. Рассмотрим следующие группы дележей 
.
Группа а) 
: дележ 
доминируется дележом 
на коалиции 
; дележ 
доминируется дележом 
на коалиции 
; дележ 
доминируется дележом 
на коалиции 
.
Группа б) одна компонента дележа 
больше 
, а сумма двух других компонент меньше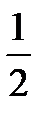 
: если 
, а 
, то дележ 
доминируется дележом 
на коалиции 
- 
; если 
, а 
, то 
; если 
, а 
, то 
.
Таким образом, указанная совокупность дележей есть решение игры по Нейману-Моргенштерну.
Пример 7. Для 
c 
найти 
и проверить, является ли С-ядро решением по Нейману-Моргенштерну;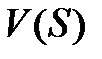 
имеет вид:
Решение.
1) Произведя нормализацию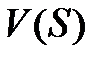 
получим
2) Дележ принадлежит 
, если 
или 
или 
Проверим условие существования непустого 
:
или 
- ядро непустое.
Геометрическая интерпретация 
приводится на рис. 15.
Рис. 15. Непустое С-ядро игры.
3) Если для 
в 0-1 редуцированной форме выполняются условия
(2.18)
то 
непустое и является решением по Нейману-Моргенштерну. Проверим условия (2.18):
а) 
- условие выполняется;
б) 
- условие не выполняется;
в) 
- условие не выполняется.
Условия (2.18) не выполняются, следовательно С-ядро не является решением по Нейману-Моргенштерну.
С-ядро не является решением по Нейману-Моргенштерну.