Как было отмечено выше, для неразвертывающихся поверхностей строятся условные развертки. Построение условной развертки F данной поверхности F выполняется в такой последовательности:
1) исходя из требуемой точности построения развертки данная поверхность F разрезается на несколько равных или примерно равных частей Fi;
2) отсеки Fi данной поверхности F аппроксимируются отсеками развертывающихся поверхностей Fi;
3) по уже рассмотренной методике выполняются приближенные развертки Fi отсеков поверхностей Fi, совокупность которых принимается за условную развертку данной поверхности F.
| Рис.13.8 |

Пример. Построить условную развертку F отсека поверхности вращения F(i,l) (рис. 13.8).
Условные развертки неразвертывающихся поверхностей вращения выполняются в основном двумя способами: способом цилиндров и способом конусов.
На данном примере рассмотрим способ цилиндров. При этом способе заданная поверхность F “разрезается” плоскостями Si, проходящими через ее ось i. Каждую часть заменяют отсеком касательно цилиндрической поверхности Fi, которая касается Fi вдоль ее среднего меридиана. Поверхность цилиндра Fi как и часть поверхности вращения ограничена плоскостями Si. При этом дуги параллелей поверхности F аппроксимируются отрезками образующих поверхностей цилиндров Fi.
На рис. 13.8 поверхность F “разрезается” на шесть частей. Одна из частей, средним меридианом которой является главный меридиан SA, заменена фронтально проецирующей цилиндрической поверхностью Fi, образующие которой ограничены плоскостями S и S¢.
Для приближенного построения развертки отсека поверхности цилиндра Fi ее направляющая AS, являющаяся одновременно нормальным сечением, аппроксимирована ломаной ABCDES. Развертку отсека поверхности цилиндра Fi строим по способу нормальных сечений для чего спрямляем ломаную ABCDES в отрезок прямой `A`B`C`D`E`S. Через точки `A,`B,`C.... проводим прямые перпендикулярные `A`S, на которых откладываем отрезки касательных, проведенных к соответствующим параллелям и ограниченных плоскостями S и S¢. Концы отрезков соединим плавной кривой линией. Таким образом получим лепестки плоскостей, которые определят развертку дважды аппроксимированной поверхности F.
Вопросы для самопроверки к лекции 13:
1. Что называется разверткой?
2. Какие свойства развертки Вы знаете?
3. Какие развертки применяются на практике?
4. Какими способами строятся развертки гранных поверхностей?
5. Каков порядок построения приближенных разверток?
6. Развертки каких поверхностей и как строятся условно?
ЛЕКЦИЯ 14
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Основные понятия и определения
Во многих случаях при выполнении технических чертежей оказывается необходимым иметь наряду с комплексным чертежом оригинала и более наглядное его изображение, обладающее свойством обратимости. С этой целью применяется чертеж, состоящий только из одной параллельной проекции данного оригинала, дополненной проекцией пространственной системы координат, к которой предварительно отнесен изображаемый оригинал. Такой метод получения однопроекционного обратимого чертежа называется аксонометрическим методом.
Таким образом, построение аксонометрических проекций сводится к применению координатного метода на проекционном чертеже. Так как при пользовании координатным методом приходится производить измерения по координатным осям, то отсюда и получил свое название рассматриваемый метод.
Слово аксонометрия означает буквально осеизмерение.
Проведем построение аксонометрического изображения на примере с точкой А, отнесенной к натуральной системе координат Охyz (рис. 14.1).
Точка А связывается с системой координат Охyz посредством натуральной координатной ломаной АА1АхО, где [ОАх]=хА, [АхА1]=yА, [А1А]=zA, суть координаты точки А,  измеренные натуральным единичным (масштабным) отрезком l.
измеренные натуральным единичным (масштабным) отрезком l.
| Рис.14.1 |
Проекция А¢ точки А на П¢ называется аксонометрической проекцией, П¢ - плоскостью аксонометрических проекций, проекция О¢х¢y¢z¢- аксонометрической системой координат, проекция А¢1 точки А¢ - вторичной проекцией, А¢А¢1А¢хО¢ - аксонометрической координатной ломаной, проекции l¢x, l¢y, l¢z - аксонометрическими единичными (масштабными) отрезками. Из свойств параллельного проецирования следует:
по хА-  ; по уА-
; по уА-  ; по zА-
; по zА- 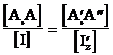

что определяет обратимость аксонометрического чертежа.
Искажения по аксонометрическим осям определяются показателями искажения, равными отношениям аксонометричных единичных отрезков к натуральному их значению
 ;
;  ;
; 
В зависимости от вида проецирования аксонометрии бывают центральные, параллельные (косоугольные) и прямоугольные (ортогональные). В последнем случае направление проецирования s перпендикулярно плоскости П¢.
В зависимости от соотношения между показателями искажения аксонометрии называются:
1) изометрическая (все показатели искажения равны);
2) диметрическая (два показателя искажения равны, но не равны третьему);
3) триметрическая (все показатели искажения различны).
При построении аксонометрических изображений необходимо знать насколько произвольно могут быть выбраны аксонометрические оси и аксонометрические единичные отрезки. На этот вопрос отвечает основная теорема аксонометрии, называемая также теоремой Польке. Она утверждает, что в косоугольной аксонометрии выбор аксонометрических осей и единичных отрезков l¢x, l¢y, l¢z совершенно произволен.
Таким образом, на основании этой теоремы мы также можем утверждать, что изображение, полученное заданием на плоскости П¢ трех произвольных лучей О¢x¢, О ¢y¢, О ¢z¢ и отложением на них отрезков l¢x, l¢y, l¢z произвольной длины, может рассматриваться как параллельная проекция трех взаимно перпендикулярных осей системы координат Оxyz c отложенными на них равными единичными отрезками l.