На основе данных выданных преподавателем необходимо:
1. Определить параметры следующих уравнений регрессии:
а) линейного;
б) гиперболического;
в) степенного;
г) показательного (экспоненциального);
д) логарифмического;
е) параболического.
2. Оценить качество каждой модели взаимосвязи с помощью средней ошибки аппроксимации и показателя детерминации.
3. На основании результатов, полученных в пункте 2, выбрать уравнение регрессии, наилучшим образом описывающее взаимосвязь между фактором х и результативным признаком у.
4. По выбранной модели взаимосвязи сделать точечный прогноз для значения фактора равного  .
.
Определение параметров уравнений регрессии
Линейное уравнение регрессии

Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами

Решение системы:

Построенное уравнение регрессии:


Рис. 1. График линейного уравнения регрессии
Гиперболическое уравнение регрессии
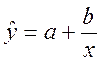
Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами
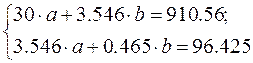
Решение системы:

Построенное уравнение регрессии:

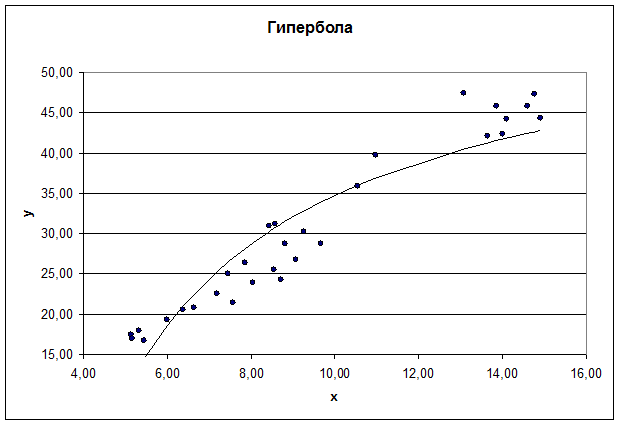
Рис. 2. График гиперболического уравнения регрессии
Степенное уравнение регрессии

Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами
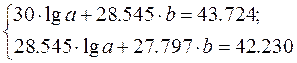
Решение системы:
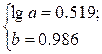

Построенное уравнение регрессии:


Рис. 3. График степенного уравнения регрессии
Показательное уравнение регрессии
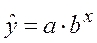
Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами

Решение системы:

 ;
;

Построенное уравнение регрессии:


Рис. 4. График показательного уравнения регрессии
Логарифмическое уравнение регрессии

Система нормальных уравнений в общем виде:
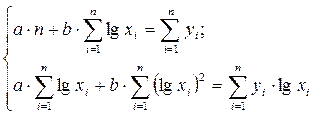
Система нормальных уравнений с вычисленными коэффициентами

Решение системы:

Построенное уравнение регрессии:


Рис. 5. График логарифмического уравнения регрессии
Параболическое уравнение регрессии

Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами

Решение системы:

Построенное уравнение регрессии:
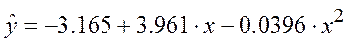

Рис. 6. График параболического уравнения регрессии
Оценка качества построенных уравнений регрессии
Средняя ошибка аппроксимации:

Показатель детерминации:

| Название | Уравнение | A, % | R2 |
| Линейная | 
| 5.765 | 0.950 |
| Гипербола | 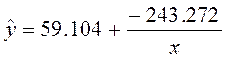
| 11.839 | 0.867 |
| Степенная | 
| 5.758 | 0.951 |
| Показательная | 
| 7.152 | 0.921 |
| Логарифмическая | 
| 7.862 | 0.934 |
| Параболическая | 
| 5.904 | 0.952 |
Выбор уравнения регрессии
На основании результатов, полученных в пункте 2, можно сделать вывод, что наиболее подходящими для описания взаимосвязи между результативной переменной у и фактором х являются функции: параболическая, степенная и линейная, поскольку эти функции имеют наиболее близкие к единице значения показателя детерминации. Для дальнейших вычислений выберем линейную функцию, как наиболее простую, и в то же самое время не уступающую по качеству двум другим выделенным ранее.