ДЕПАРТАМЕНТ образования ГОРОДА МОСКВЫ
МОСКОВСКИЙ ГОРОДСКОЙ
ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ Психологического Консультирования
ПСИХОГЕНЕТИКА
Проектная курсовая лабораторная работа
Измерение количественных признаков.
Построение распределений.
Вычисление основных статистик.
Подсчет корреляций между признаками и между
родственниками. Ассортативность
Выполнила студентка
Нестерова М.С.
Группа 2.1
Преподаватель,
ведущий семинары
Николаева Н.А
Дата сдачи работы 23 апреля 2012
Подпись преподавателя ______________
2012, апрель
Введение
Данная работа посвящена нахождению взаимозависимости между некоторыми физическими и психологическими признаками. Первая часть работы является описанием корреляции на примере группы студентов, то есть является учебной ситуацией. Вторая часть является реальным экспериментом, проведённым на семьях студентов. Здесь изучаются рост, вес, пищевое поведение, избегание вреда, направленность личности и степень сотрудничества всех членов семей, участвующих в данном исследовании.
Часть 1
Учебная ситуация
Измерение и статистическое описание количественных
признаков
| i | Фамилия, инициалы | № (пары) | Рост стоя (см) хi | Рост сидя (см) уi | _ (хi-х)2 | _ (уi-у)2 | |
| Михайлова А.А. | Р | 85,38 | 8,7 | ||||
| Дубова Т.В. | О | 1,54 | 0,9 | ||||
| Устинова Н.А. | Р | 202,78 | 48,3 | ||||
| Янченкова Т.Д. | О | 1,54 | 1,1 | ||||
| Ягафарова М.И. | Р | 1,54 | 4,2 | ||||
| Соколова А.В. | О | 7,62 | 0,9 | ||||
| Тарасенко Л.В. | Р | 27,46 | 24,5 | ||||
| Выскребенцева С.А. | О | 27,46 | 8,7 | ||||
| Савчук А.И. | Р | 17,98 | 15,6 | ||||
| Анисимова Е.В. | О | 5,02 | 4,2 | ||||
| Нестерова М.С. | Р | 22,66 | 9,3 | ||||
| Чешуина Т.А. | О | 10,5 | 0,9 | ||||
| Овчинникова Н.Д. | Р | 10,5 | 3,8 | ||||
| Пащенко А.В. | О | 315,42 | 49,7 | ||||
| Бельская О.И. | Р | 27,46 | 48,3 | ||||
| Позднякова П.Н. | О | 27,46 | 15,6 | ||||
| Тихонова А.Н. | Р | 52,42 | 8,7 | ||||
| Ануфриева А.В. | О | 22,66 | 1,1 | ||||
| Крохин А.А. | Р | 0,06 | 4,2 | ||||
| Якимович И.А. | О | 390,46 | 49,7 | ||||
| Каширин В.Г. | Р | 351,94 | 226,5 | ||||
| N=21 | Среднее | 170,24 | 67,95 | ∑=1609,86 | ∑=534,9 |
σ21=  =
=  =80,49
=80,49
σ22=  =
=  =26,75
=26,75
Таблицы для разбиения на классы
(для величин роста стоя и роста сидя)
Таблица 1.1
Разбиение на классы с шагом 6 см
| Классы | Рост стоя (х) | Рост сидя (у) | ||
| См | Число людей | См | Число людей | |
| 156-161 | 61-66 | |||
| 162-167 | 67-72 | |||
| 168-173 | 73-78 | |||
| 174-179 | 79-84 | |||
| 180-185 | ||||
| 186-191 |
Рисунок 1
График распределения для роста стоя с шагом 6 см

1) 156 см – 161 см;
2) 162 см – 167 см;
3) 168 см – 173 см;
4) 174 см – 179 см;
5) 180 см – 185 см;
6) 186 см – 191 см.
Рисунок 2
График распределения для роста сидя с шагом 6

1) 61 см – 66 см;
2) 67 см – 72 см;
3) 73 см – 78 см;
4) 79 см – 84 см.
Таблица 1.2
Разбиение на классы с шагом 3 см
| Классы | Рост стоя (х) | Рост сидя (у) | ||
| См | Число людей | См | Число людей | |
| 156-158 | 61-63 | |||
| 159-161 | 64-66 | |||
| 162-165 | 67-69 | |||
| 165-167 | 70-72 | |||
| 168-170 | 73-75 | |||
| 171-173 | 76-78 | |||
| 174-176 | 79-81 | |||
| 177-179 | 82-84 | |||
| 180-182 | ||||
| 183-185 | ||||
| 186-188 | ||||
| 189-191 |
Рисунок 3
График распределения для роста стоя с шагом 3

1) 156 см – 158 см;
2) 159 см – 161 см;
3) 162 см – 164 см;
4) 165 см – 167 см;
5) 168 см – 170 см;
6) 171 см – 173 см;
7) 174 см – 176 см;
8) 177 см – 179 см;
9) 180 см – 182 см;
10) 183 см – 185 см;
11) 186 см – 188 см;
12) 189 см – 191 см.
Рисунок 4
График распределения для роста сидя с шагом 3

1) 61 см – 63 см;
2) 64 см – 66 см;
3) 67 см – 69 см;
4) 70 см – 72 см;
5) 73 см – 75 см;
6) 76 см – 78 см;
7) 79 см – 81 см;
8) 82 см – 84 см.
Расчёт коэффициента корреляции между количественными признаками
(фенотипическая корреляция)
N – число испытуемых;
_
х – среднее по всем значениям хi;
_
у – среднее по всем значениям уi;
хi – i-тое измерение роста стоя;
уi – i-тое измерение роста сидя.
Таблица 2
| i | Данные измерений | _ (хi-х) | _ (уi-у) | _ _ (хi-х)(уi-у) | _ (хi-х)2 | _ (уi-у)2 | |
| хi | уi | ||||||
| -9,24 | -2,95 | 27,26 | 85,38 | 8,7 | |||
| -1,24 | -0,95 | 1,18 | 1,54 | 0,9 | |||
| -14,24 | -6,95 | 98,97 | 202,78 | 48,3 | |||
| -1,24 | 1,05 | -1,3 | 1,54 | 1,1 | |||
| -1,24 | 2,05 | -2,54 | 1,54 | 4,2 | |||
| 2,76 | -0,95 | -2,62 | 7,62 | 0,9 | |||
| -5,24 | -4,95 | 25,94 | 27,46 | 24,5 | |||
| -5,24 | -2,95 | 15,46 | 27,46 | 8,7 | |||
| -4,24 | -3,95 | 16,75 | 17,98 | 15,6 | |||
| -2,24 | 2,05 | -4,59 | 5,02 | 4,2 | |||
| 4,46 | 3,05 | 14,52 | 22,66 | 9,3 | |||
| -3,24 | -0,95 | 3,08 | 10,5 | 0,9 | |||
| -3,24 | -1,95 | 6,32 | 10,5 | 3,8 | |||
| 17,76 | 7,05 | 125,21 | 315,42 | 49,7 | |||
| -5,24 | -6,95 | 36,42 | 27,46 | 48,3 | |||
| -5,24 | -3,95 | 20,7 | 27,46 | 15,6 | |||
| -7,24 | -2,95 | 21,36 | 52,42 | 8,7 | |||
| 4,76 | 1,05 | 22,66 | 1,1 | ||||
| -0,24 | 2,05 | -0,49 | 0,06 | 4,2 | |||
| 19,76 | 7,05 | 139,31 | 390,46 | 49,7 | |||
| 18,76 | 15,05 | 282,32 | 351,94 | 226,5 | |||
| N=21 | _ х=170,24 | _ у=67,95 | ∑=828,28 | ∑=1609,86 | ∑=534,9 |
r=  =
=  =
=  =
=  =
=  =0,89
=0,89
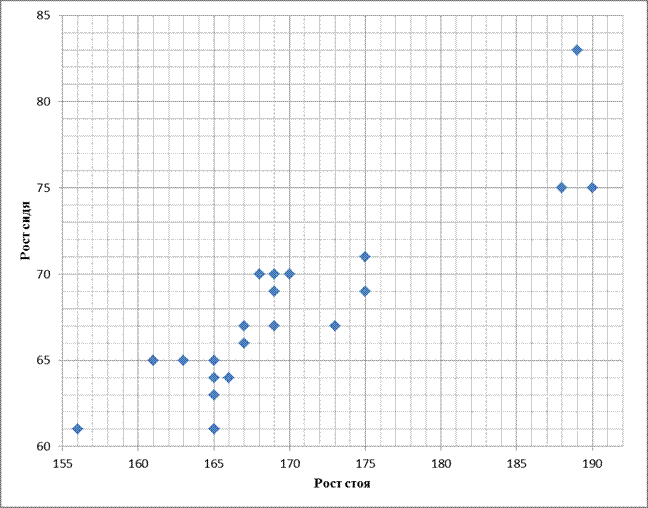
Рисунок 5
Графическое отображение фенотипической корреляции
Таблицы расчётов коэффициента корреляции между
«родственниками» в парах «родитель-ребёнок»
Таблица 3.1
Изучаемый признак: рост стоя
N – число испытуемых;
_
х – среднее по всем значениям хi;
_
у – среднее по всем значениям уi;
хi – измерение родителя i-той паре;
уi – измерение ребёнка i-той паре.
| i | «Родитель» (Р) (Ф.И.О.) | «Ребёнок» (О) (Ф.И.О) | хi | уi | _ (хi-х) | _ (уi-у) | _ _ (хi-х)(уi-у) | _ (хi-х)2 | _ (уi-у)2 |
| Михайлова А.А. | Дубова Т.В. | -4,7 | -3,9 | 18,33 | 22,09 | 15,21 | |||
| Устинова Н.А. | Янченкова Т.Д. | -9,7 | -3,9 | 37,83 | 94,09 | 15,21 | |||
| Ягафарова М.И. | Соколова А.В. | 3,3 | 0,1 | 0,33 | 10,89 | 0,01 | |||
| Тарасенко Л.В. | Выскребенцева С.А. | -0,7 | -7,9 | 5,53 | 0,49 | 62,41 | |||
| Савчук А.И. | Анисимова Е.В. | 0,3 | -4,9 | -1,47 | 0,09 | 24,01 | |||
| Нестерова М.С. | Чешуина Т.А. | 9,3 | -5,9 | -49,29 | 86,49 | 34,81 | |||
| Овчинникова Н.Д. | Пащенко А.В. | 1,3 | 15,1 | 19,63 | 1,69 | 228,01 | |||
| Бельская О.И. | Позднякова П.Н. | -0,7 | -7,9 | 5,53 | 0,49 | 62,41 | |||
| Тихонова А.Н. | Ануфриева А.В. | -2,7 | 2,1 | -5,67 | 7,29 | 4,41 | |||
| Крохин А.А. | Якимович И.А. | 4,3 | 17,1 | 73,53 | 18,49 | 292,41 | |||
| N=10 | _ х=165,7 | _ у =172,9 | ∑=104,28 | ∑=242,04 | ∑=738,9 |
r1=  =
=  =
=  =
=  =
=  =0,25
=0,25
Рисунок 6
Графическое отображение корреляции между «родственниками»
(рост стоя)

Таблица 3.2
Изучаемый признак: рост сидя
N – число испытуемых;
_
х – среднее по всем значениям хi;
_
у – среднее по всем значениям уi;
хi – измерение родителя i-той паре;
уi – измерение ребёнка i-той паре.
| i | «Родитель» (Р) (Ф.И.О.) | «Ребёнок» (О) (Ф.И.О) | хi | уi | _ (хi-х) | _ (уi-у) | _ _ (хi-х)(уi-у) | _ (хi-х)2 | _ (уi-у)2 |
| Михайлова А.А. | Дубова Т.В. | -0,6 | -1,8 | 1,08 | 0,36 | 3,24 | |||
| Устинова Н.А. | Янченкова Т.Д. | -4,6 | 0,2 | -0,92 | 21,16 | 0,04 | |||
| Ягафарова М.И. | Соколова А.В. | 4,4 | -1,8 | -7,92 | 19,36 | 3,24 | |||
| Тарасенко Л.В. | Выскребенцева С.А. | -2,6 | -3,8 | 9,88 | 6,76 | 14,44 | |||
| Савчук А.И. | Анисимова Е.В. | -1,6 | 1,2 | -1,92 | 2,56 | 1,44 | |||
| Нестерова М.С. | Чешуина Т.А. | 5,4 | -1,8 | -9,72 | 29,16 | 3,24 | |||
| Овчинникова Н.Д. | Пащенко А.В. | 0,4 | 6,2 | 2,48 | 0,16 | 38,44 | |||
| Бельская О.И. | Позднякова П.Н. | -4,6 | -4,8 | 22,08 | 21,16 | 23,04 | |||
| Тихонова А.Н. | Ануфриева А.В. | -0,6 | 0,2 | -0,12 | 0,36 | 0,04 | |||
| Крохин А.А. | Якимович И.А. | 4,4 | 6,2 | 27,28 | 19,36 | 38,44 | |||
| N=10 | _ х=65,6 | _ у =68,8 | ∑=42,2 | ∑=120,4 | ∑=738,9 |
r=  =
=  =
=  =
=  =
=  =0,34
=0,34
Рисунок 7
Графическое отображение корреляции между «родственниками»
(рост сидя)

Часть 2
Экспериментальная ситуация
2. Корреляции между признаками
Изучаемый признак: рост – вес.

Коэффициент корреляции Пирсона: 0,319
Корреляция значима на уровне 0,01 (2сторонняя)
Средняя, прямая.
Чем выше рост, тем выше вес.

Коэффициент корреляции Пирсона: 0,461
Корреляция значима на уровне 0,01 (2сторонняя)
Средняя, прямая.
Чем выше рост, тем выше вес.

Коэффициент корреляции Пирсона: 0,233
Корреляция значима на уровне 0,01 (2сторонняя)
Низкая, прямая.
Чем выше рост, тем выше вес.

Коэффициент корреляции Пирсона: 0, 305
Корреляция значима на уровне 0,01 (2сторонняя)
Средняя, прямая.
Чем выше рост, тем выше вес.
Изучаемый признак: пищевое поведение – направленность личности.

Коэффициент корреляции Пирсона: -0,101
Пищевое поведение не зависит от направленности личности.

Коэффициент корреляции Пирсона: -0,344
Корреляция значима на уровне 0,01 (2сторонняя)
Средняя, обратная.
Чем активнее пищевое поведение, тем ниже направленность личности.

Коэффициент корреляции Пирсона: -0,281
Корреляция значима на уровне 0,01 (2сторонняя)
Низкая, обратная.
Чем активнее пищевое поведение, тем ниже направленность личности.

Коэффициент корреляции Пирсона: -0,118
Пищевое поведение не зависит от направленности личности.
3. Корреляции между родственниками
Изучаемый признак: пищевое поведение

Коэффициент корреляции Пирсона: 0,264
Корреляция значима на уровне 0,01 (2сторонняя)
Низкая, прямая.
Чем активнее пищевое поведение матери, тем активнее пищевое поведение дочери.
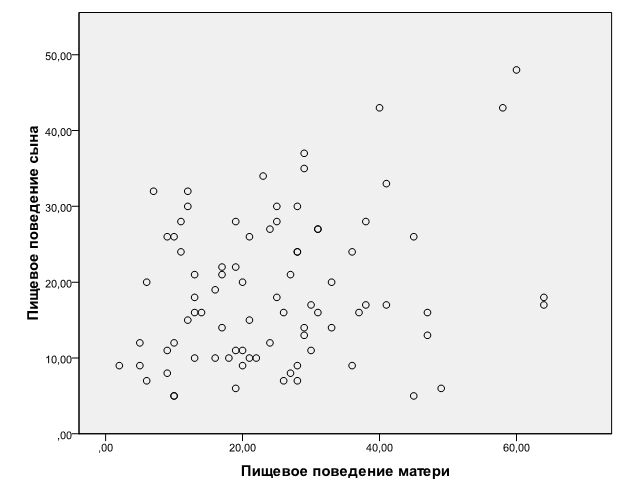
Коэффициент корреляции Пирсона: 0,254
Корреляция значима на уровне 0,05 (2сторонняя)
Низкая, прямая.
Чем активнее пищевое поведение матери, тем активнее пищевое поведение сына.

Коэффициент корреляции Пирсона: 0,047
Пищевое поведение дочери не зависит от пищевого поведения отца.

Коэффициент корреляции Пирсона: 0,086
Пищевое поведение сына не зависит от пищевого поведения отца.
Изучаемый признак: направленность личности

Коэффициент корреляции Пирсона: 0,124
Направленность личности дочери не зависит от направленности личности матери.

Коэффициент корреляции Пирсона: 0,281
Корреляция значима на уровне 0,01 (2сторонняя)
Низкая, прямая.
Чем выше направленность личности матери, тем выше направленность личности сына.

Коэффициент корреляции Пирсона: 0,085
Направленность личности дочери не зависит от направленности личности отца.

Коэффициент корреляции Пирсона: 0,099
Направленность личности сына не зависит от направленности личности отца.
Изучаемый признак: рост

Коэффициент корреляции Пирсона: 0,226
Корреляция значима на уровне 0,05 (2сторонняя)
Низкая, прямая.
Чем выше рост матери, тем выше рост дочери.

Коэффициент корреляции Пирсона: 0,476
Корреляция значима на уровне 0,01 (2сторонняя)
Средняя, прямая.
Чем выше рост матери, тем выше рост сына.
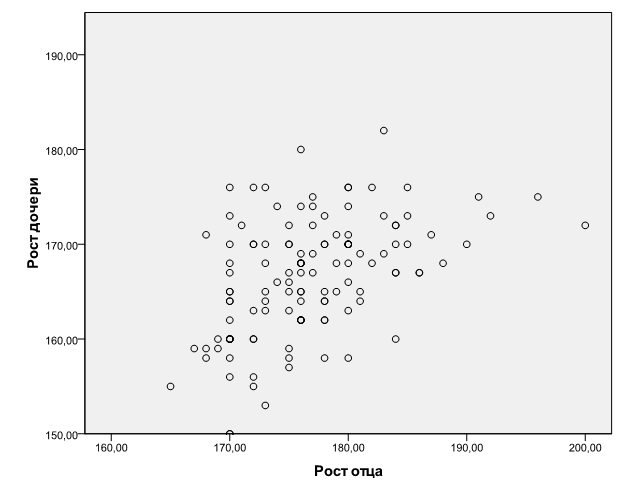
Коэффициент корреляции Пирсона: 0,472
Корреляция значима на уровне 0,01 (2сторонняя)
Средняя, прямая.
Чем выше рост отца, тем выше рост дочери.

Коэффициент корреляции Пирсона: 0,455
Корреляция значима на уровне 0,01 (2сторонняя)
Средняя, прямая.
Чем выше рост отца, тем выше рост сына