Полупроводниковые диоды
Задача I.2. В схеме, изображенной на рисунке I.1 определить ток через диоды и напряжение на каждом диоде. Определить дифференциальное сопротивление диодов R диф и сопротивление по постоянному току RП. Вольт-амперная характеристика диодов изображена на рисунке I.2.
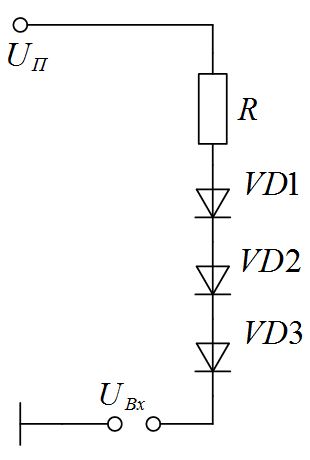
Рисунок I.1. Схема к задаче I.2
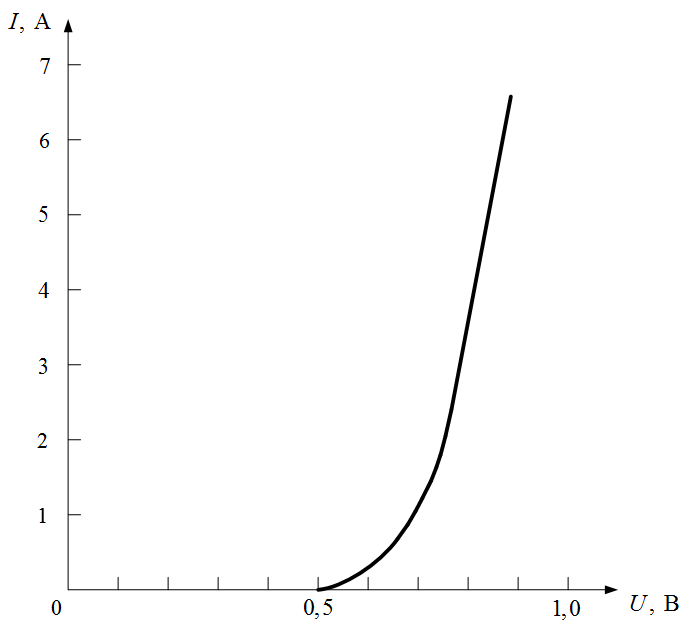
Рисунок I.2. ВАХ к задаче I.2
Расчёт номеров строк в столбцах таблиц условий задач в методичке:
Номер зачётной книжки 071518126, следовательно номером строки в столбце А является 6, в столбце В – 2, а в столбце С – 8 (6 + 2 = 8).
Исходные данные: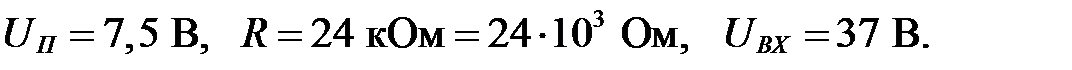 
Решение.
1. Для решения запишем 2-ой закон Кирхгофа для цепи:
В нашем случае (для рис. I.1):
так как в условии задачи дана ВАХ одна для всех трёх диодов, то выражение (1) примет вид:
Чтобы определить неизвестные I и Ud нужно ещё одно уравнение, которое можно извлечь из ВАХ диода (графически). Найдем точки пересечения заданной характеристики с осями координат, чтобы построить эту прямую. Предположив, что Id = 0, получим точку пересечения прямой с осью Uхх:
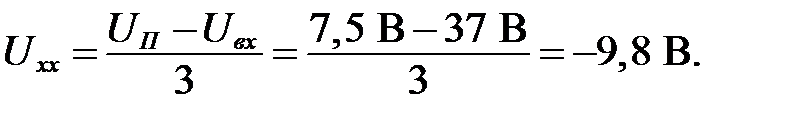
Полученное значение напряжения холостого хода отрицательно, а исходя из схемы рисунка I.1 видно, что p-n переход диода VD 3 будет закрыт. В таком режиме ток в рассматриваемой цепи будет обусловлен движением неосновных носителей заряда, которым в нашем расчете можно пренебречь, поэтому будем считать, что при входном напряжении в 37 В рассматриваемой схемы диод будет закрыт.
Ответ: Решения нет.
Задача I.3. В схеме, изображенной на рисунке I.3, определить токи через диоды и напряжение на выходе U вых. Определить дифференциальное сопротивление диодов R дифи сопротивление по постоянному току R П. Вольт-амперная характеристика диодов приведена на рисунке I.2.
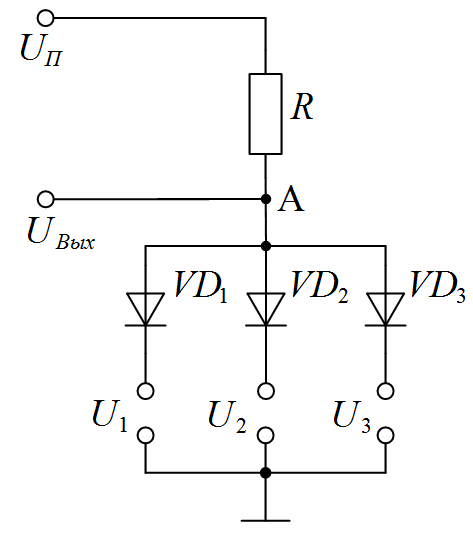
Рисунок I.3. Схема к задаче I.3
Исходные данные:
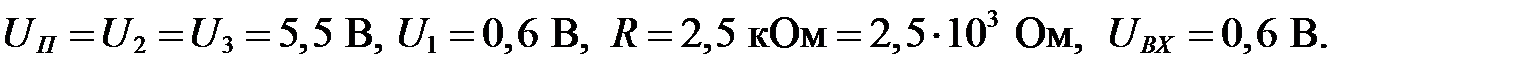
Решение.
1. Поскольку напряжения U2 и U3 – одинаковые, то напряжения на диодах VD2 и VD3 и токи через эти диоды одинаковые. Обозначим их через Ud и Id соответственно. Предположим, что диоды U2 и U3 открыты. Тогда из рисунка I.2 видно, что это возможно, если потенциал точки А превышает величину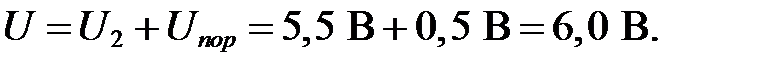 
Если это так, то напряжение на диоде VD1 окажется равным 
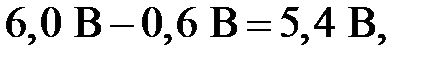что противоречит рисунку 1.2. Поэтому положим, что диоды VD2 и VD3 закрыты.
Ток I через сопротивление R в соответствии с 1-м законом Кирхгофа равен току через открытый диод: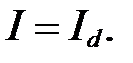 
Согласно 2-му закону Кирхгофа
Чтобы определить неизвестные Id и Ud нужно ещё одно уравнение, которое можно извлечь из ВАХ диода (графически). Найдем точки пересечения заданной характеристики с осями координат, чтобы построить эту прямую. Предположив, что Id = 0, получим точку пересечения прямой с осью Uхх:
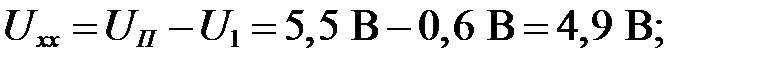
Ток короткого замыкания (точка пересечения прямой с осью ординат):
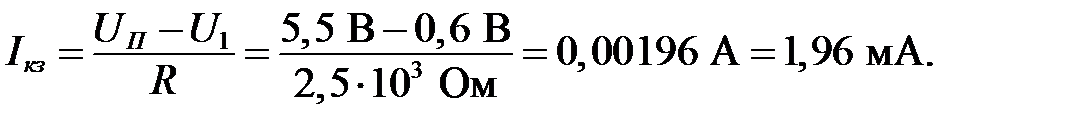
Так как полученное значение Uхх не помещается на графике (рисунок I.2), построим сначала вспомогательную прямую, параллельную нагрузочной прямой. Пусть вспомогательная прямая (II) пересекает ось напряжений в точке UII = 0,7 В, то есть UII = Uхх / 7; тогда эта прямая должна пересечь ось ординат (токов) в точке III = Iкз / 7 = 0,28мА. Проведем вспомогательную прямую через точки (0,28 мА; 0) и (0,7 В; 0) на графике (рисунок I.4).
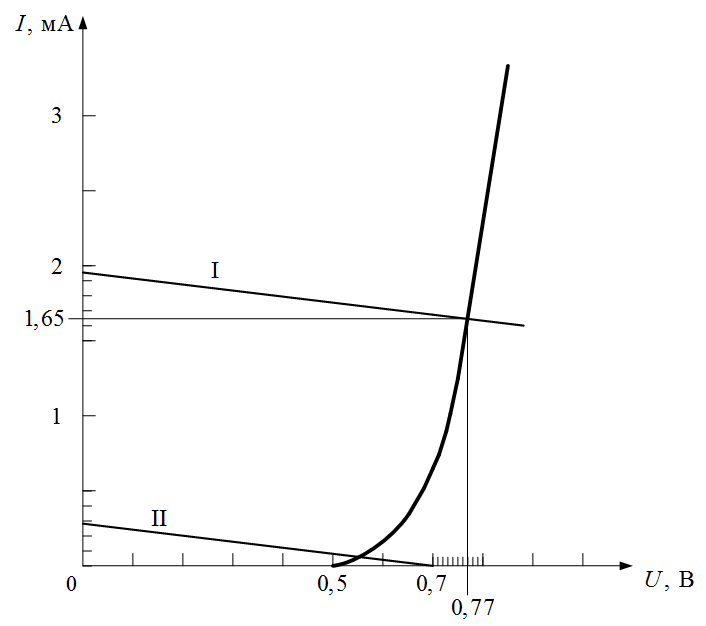
Рисунок I.4. ВАХ к задаче I.3
Нагрузочная прямая (I) пройдет через точку (0; 1,96 мА) параллельно вспомогательной.
По точке пересечения нагрузочной прямой и ВАХ диода определяем:
искомое напряжение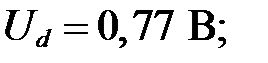 
искомый ток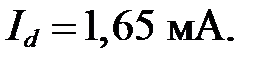 
2. Из формулы (3) напряжение на выходе схемы равно:
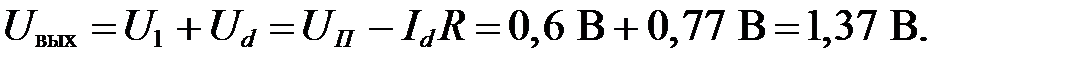
Диоды VD2 и VD3 в этом случае закрыты, как и полагалось ранее; напряжение на них равно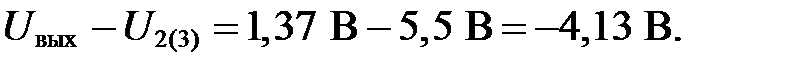 
3. Найдем сопротивления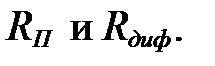 
Сопротивление постоянному току RП равно:
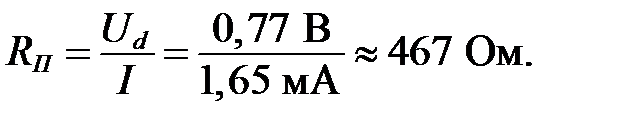
Аналогично решению задачи I.2 дифференциальное сопротивление Rдиф равно (см. рисунок I.6):
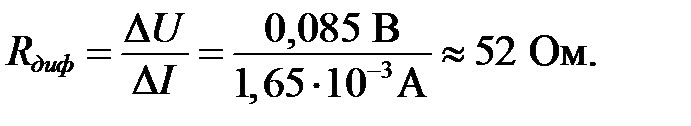
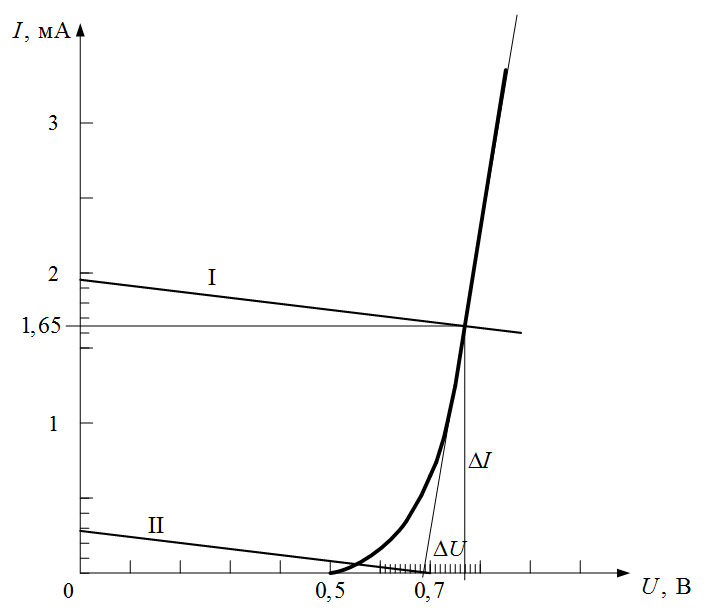
Рисунок I.5. ВАХ к задаче I.3
Ответ: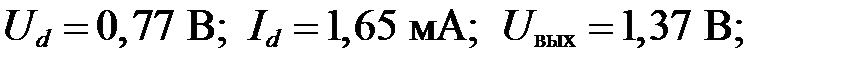 
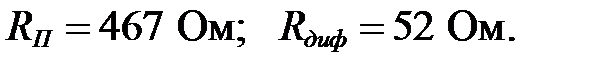
Задача I.5. В схеме на рисунке I.6 определить токи через диоды, напряжение на диодах и напряжение на выходе U вых. Определить дифференциальное сопротивление диодов Rдиф и сопротивление по постоянному току RП. Вольт-амперная характеристика диодов изображена на рисунке I.2.
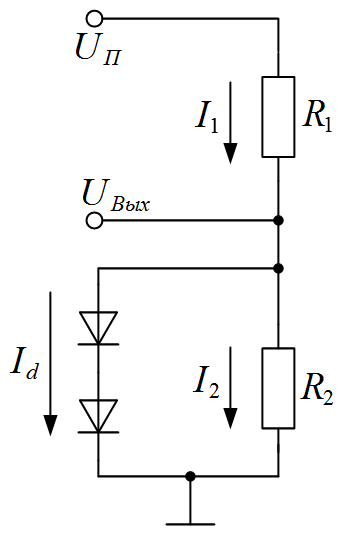
Рисунок I.6. Схема к задаче I.5
Исходные данные:
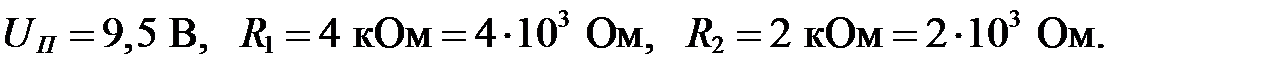
Решение.
1. Запишем уравнения по законам Кирхгофа
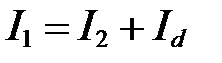
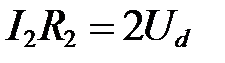
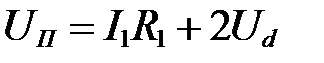
Исключая токи I 1 и I 2, получим уравнение нагрузочной прямой в виде
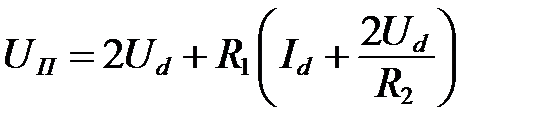
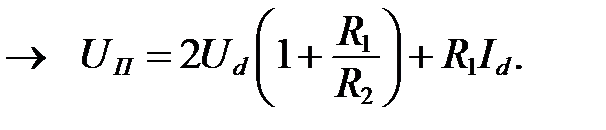
Положив, что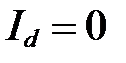 
, получим
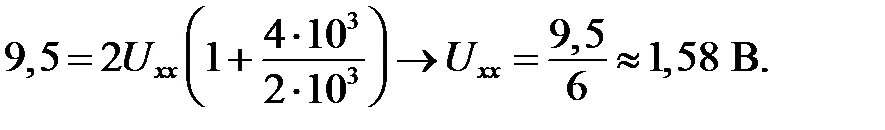
Положив, что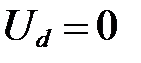 
, получим
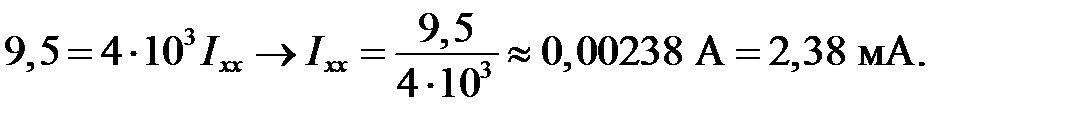
Так как полученное значение Uхх не помещается на графике (рисунок I.2), построим сначала вспомогательную прямую, параллельную нагрузочной прямой. Пусть вспомогательная прямая (II) пересекает ось напряжений в точке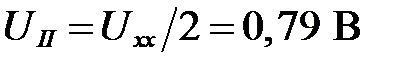 
; тогда эта прямая должна пересечь ось ординат (токов) в точке 
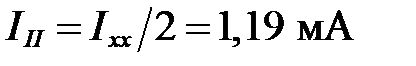. Проведем вспомогательную прямую через точки (1,19 мА; 0) и (0,79 В; 0) на графике (рисунок I.7).
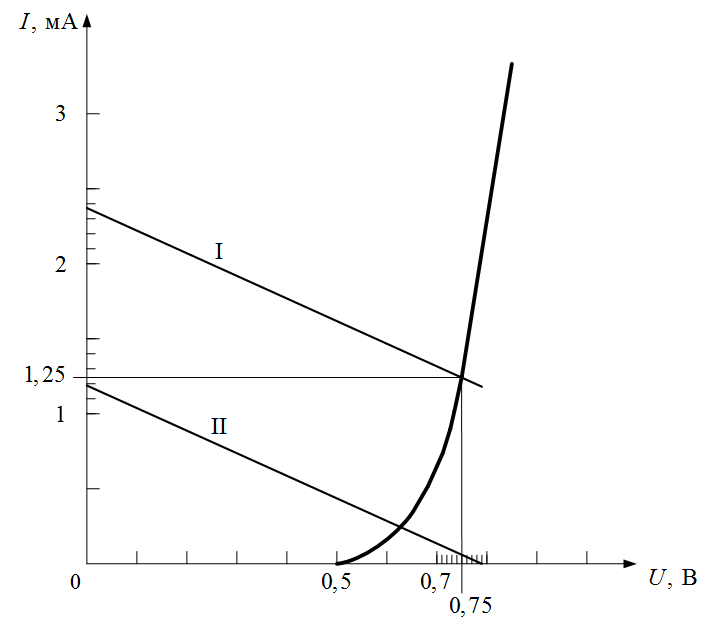
Рисунок I.7. ВАХ к задаче I.5
Нагрузочная прямая (I) пройдет через точку (0; 2,38 мА) параллельно вспомогательной.
По точке пересечения нагрузочной прямой и ВАХ диода определяем:
искомое напряжение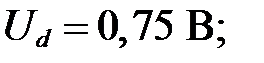 
искомый ток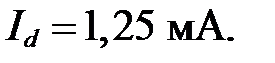 
2. Напряжение на выходе схемы равно:
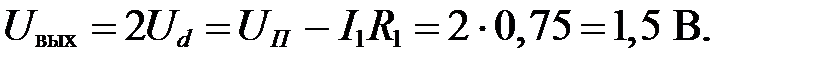
Проверка
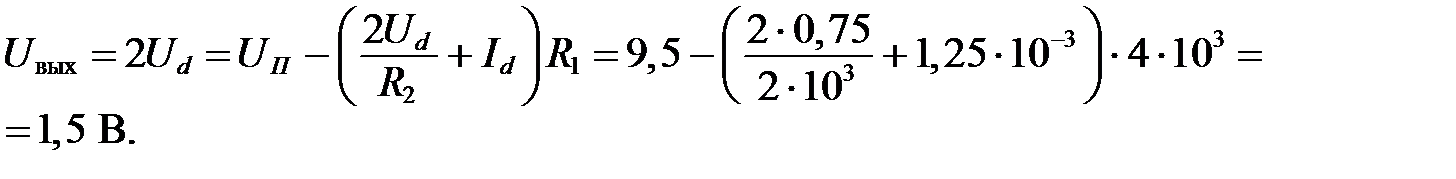
3. Найдем сопротивления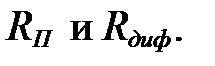
Сопротивление постоянному току RП равно:
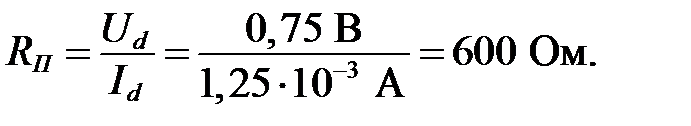
Аналогично решению задачи I.2 дифференциальное сопротивление Rдиф равно (см. рисунок I.8):
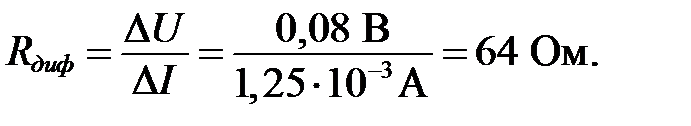
Рисунок I.8. ВАХ к задаче I.5
Ответ: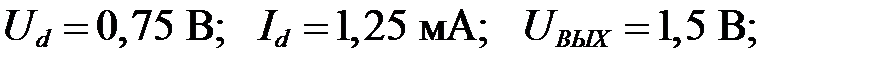 
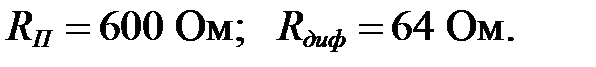
Задача I.7. Определить токи I 1 , I 2 , I 3 , I 4 , I 5 в схеме, изображенной на рисунке I.9. Диоды VD1-VD5 одинаковые, их вольт-амперная характеристика приведена на рисунке I.10.
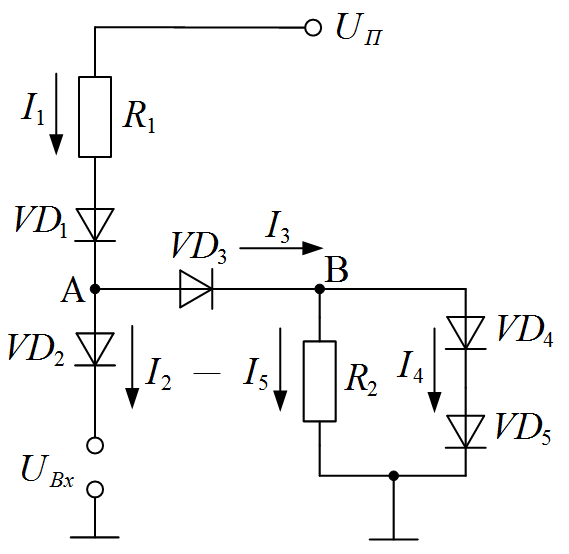
Рисунок I.9. Схема к задаче I.7
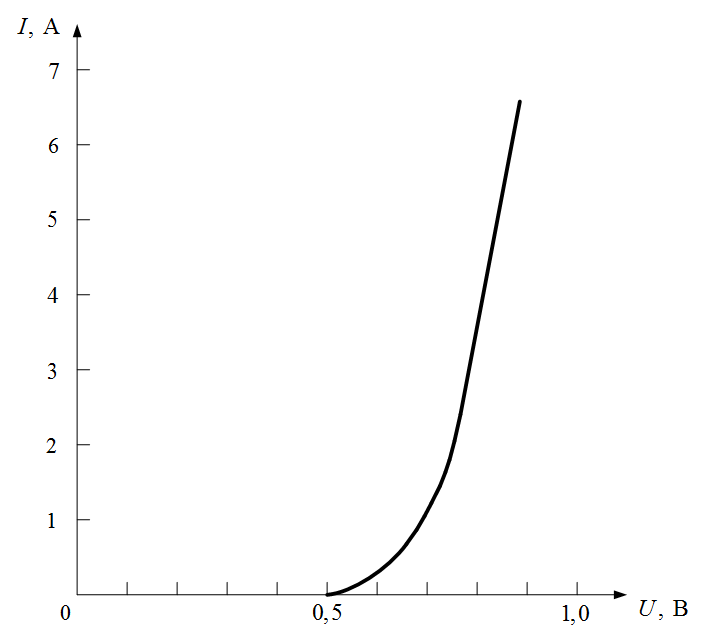
Рисунок I.10. ВАХ к задаче I.7
Исходные данные:
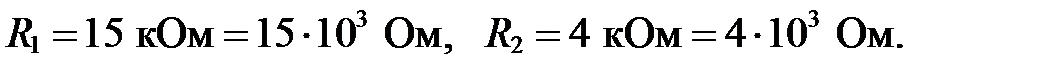
Решение.
1. Сначала определим, по каким ветвям протекает ток, а по каким он протекать не может. Предположив, что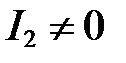 
, оценим потенциал в точке А, который не может быть менее:
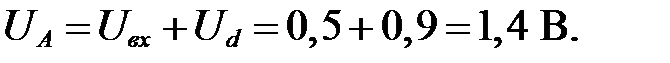
Потенциал в точке А, достаточный для открытия диодов VD 3 VD 4 и VD 5 составит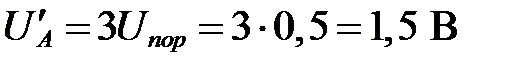 
, значит ток через них при 
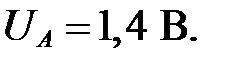не пойдет. При открытых диодах VD 3 VD 4 и VD 5 что потенциал в точке А равен:
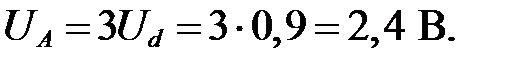
Положим, что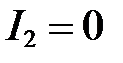 
, тогда
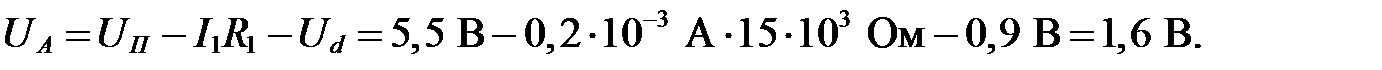
Отсюда следует, что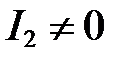 
. Тогда потенциал в точке А будет равен:
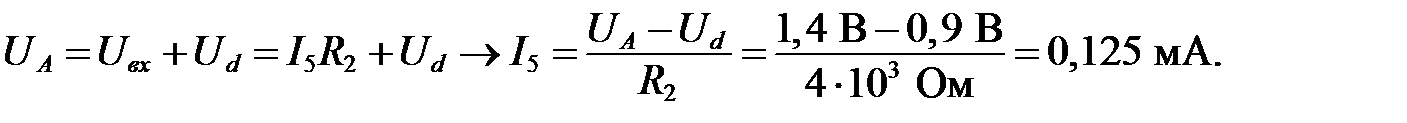
По второму закону Кирхгофа
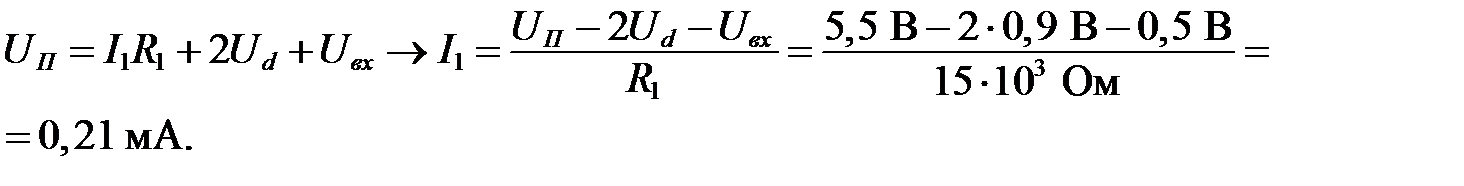
При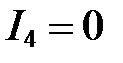 
(диоды VD 4 и VD 5 закрыты), по первому закону Кирхгофа
, тогда
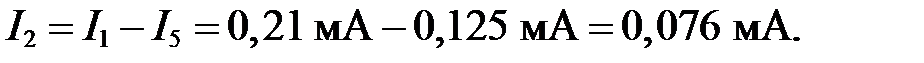
Ответ: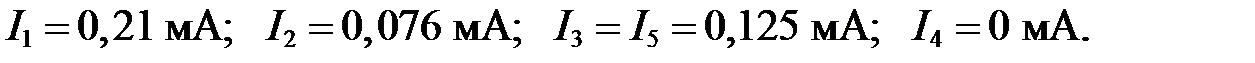 
Задача I.9. Определить токи I 1 , I 2 , I 3 , I 4 , I 5 в схеме, изображенной на рисунке I.11. Диоды VD 1- VD 6 одинаковые.
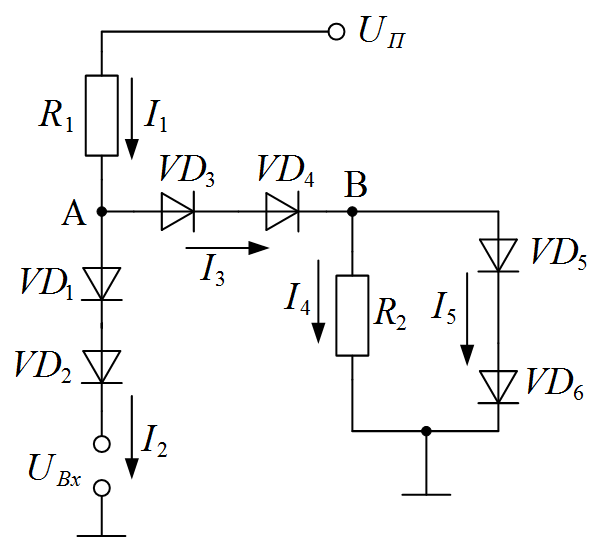
Рисунок I.11. Схема к задаче I.9
Исходные данные:
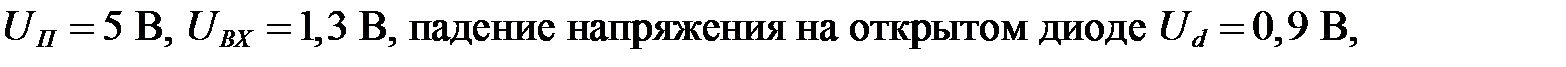
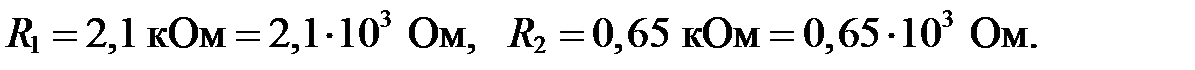
Решение.
1. Предположим, что ток 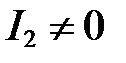. Тогда потенциал в точке разветвления будет равен 
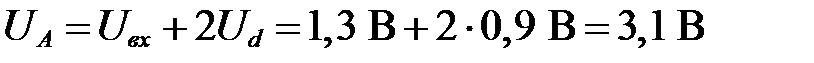. Предположим, что ток 
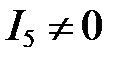. В этом случае потенциал точки разветвления равен 
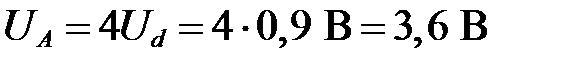. Предположим, что 
:
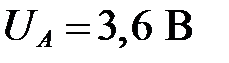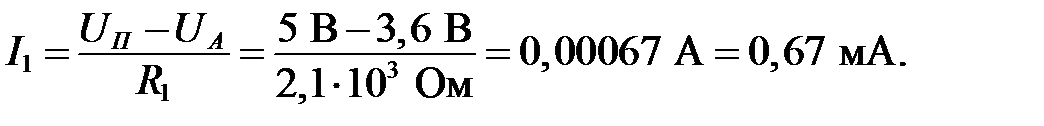
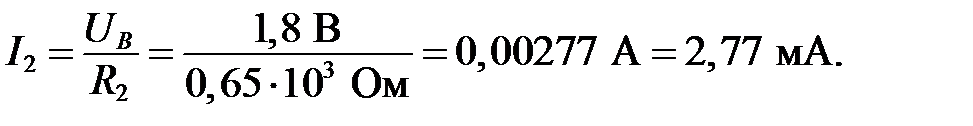
Согласно схеме, ток I 4 не может быть больше тока I 1. Отсюда следует, что предположение о том, что 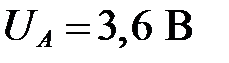, неверно.
Предположим, что,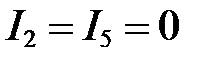 
, а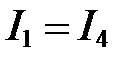 
, тогда:
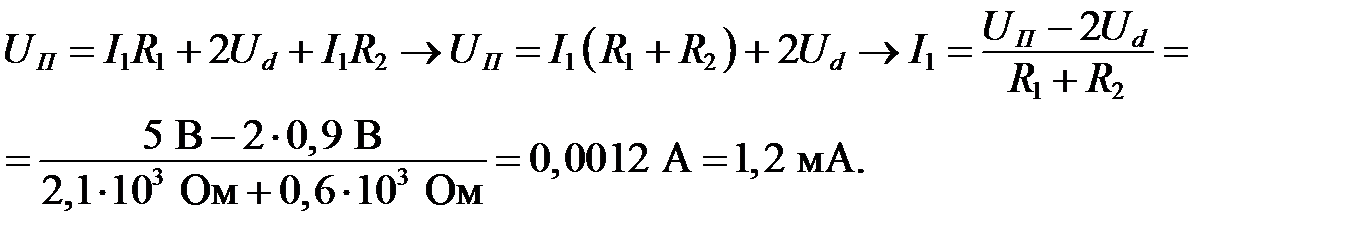
Ответ: 
Полупроводниковый стабилитрон
Задача (I.10).
1. В соответствие с исходными данными выбрать стабилитрон. Принципиальная схема параметрического стабилизатора представлена на рисунке I.12.
2. Выбрать балластное сопротивление R б.
3. Уточнить балластное сопротивление по ряду Е24.
4. Рассчитать мощности на стабилитроне, на балластном сопротивлении и КПД стабилизатора.
5. Рассчитать коэффициент стабилизации.
6. Построить ВАХ стабилизатора.
7. Выполнить проверочный расчет.
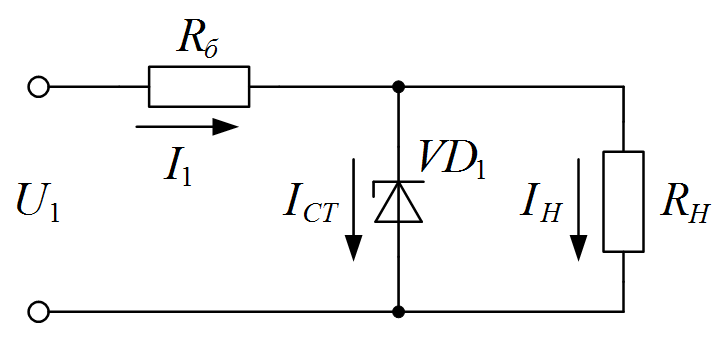
Рисунок I.12. Принципиальная схема параметрического стабилизатора напряжения
Исходные данные: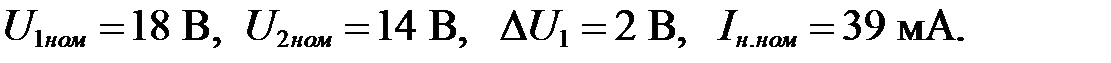 
Решение.
1. Руководствуюсь исходными данными по справочнику [5] выбираем стабилитрон с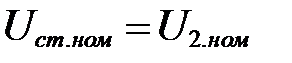 
. В нашем случае это стабилитрон типа КС509А со следующими паспортными данными:
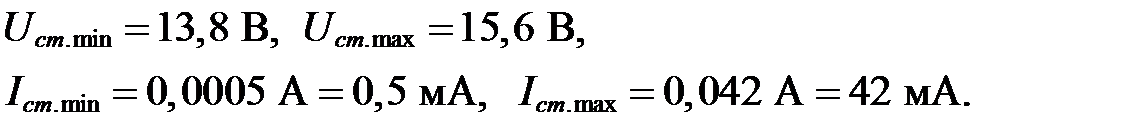
2. Определяем сопротивление нагрузки:
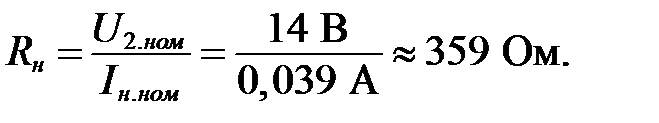
Ток и напряжение в цепи параметрического стабилизатора:
где Rб – сопротивления балластного резистора.
Составим систему неравенств для определения балластного сопротивления:
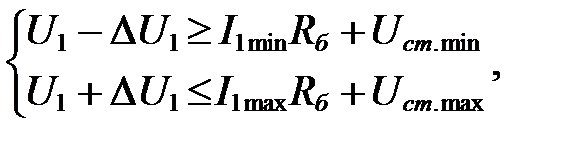
где
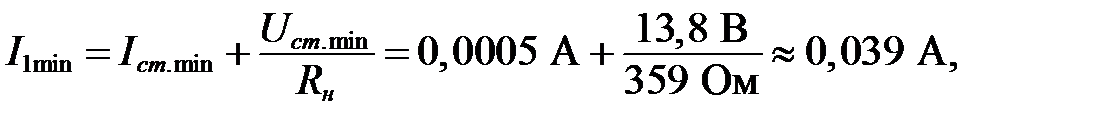
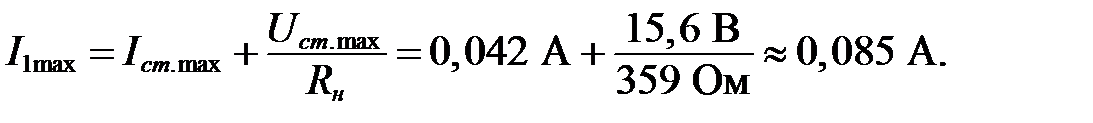
Тогда
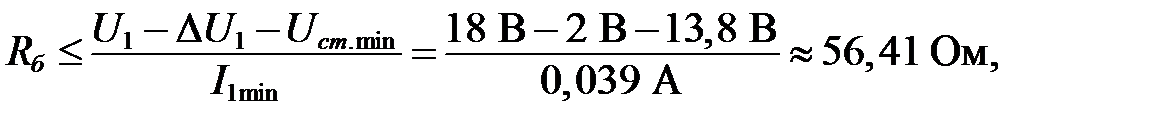
3. Уточняем по ряду сопротивлений постоянных резисторов Е24 балластное сопротивление стабилитрона:
.
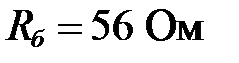4. Определяем параметры стабилизатора в соответствии с выбранным балластным сопротивлением. В номинальном режиме:
.
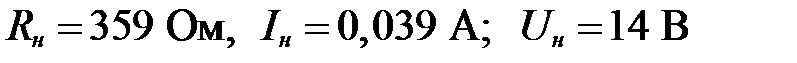Мощность, потребляемая от сети питания:
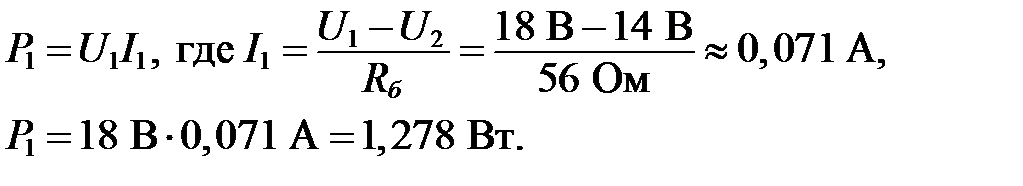
Мощность, передаваемая нагрузке:
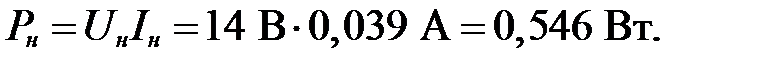
КПД параметрического стабилизатора:
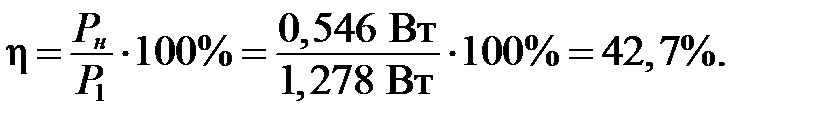
5. Коэффициент стабилизации:
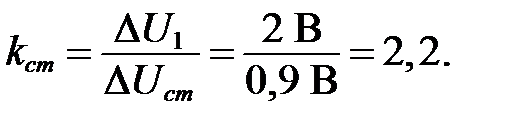
Выполним проверочный расчет. Для этого составляем схему замещения (рисунок I.13), заменив в принципиальной схеме стабилизатора стабилитрон на последовательно включенные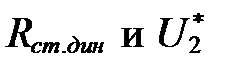 
.
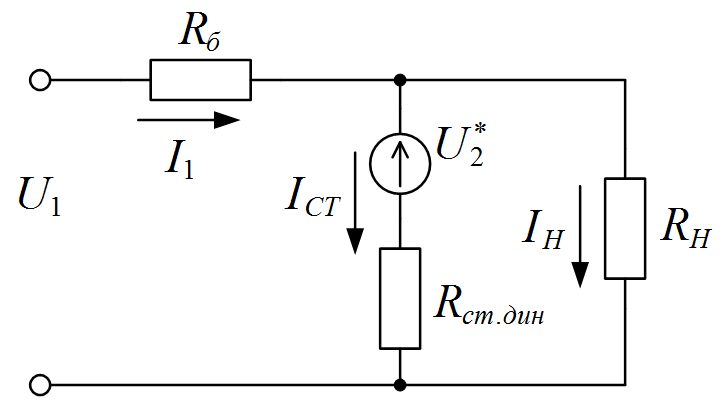
Рисунок I.13 к задаче (I.10). Сема замещения
6. Строим ВАХ:
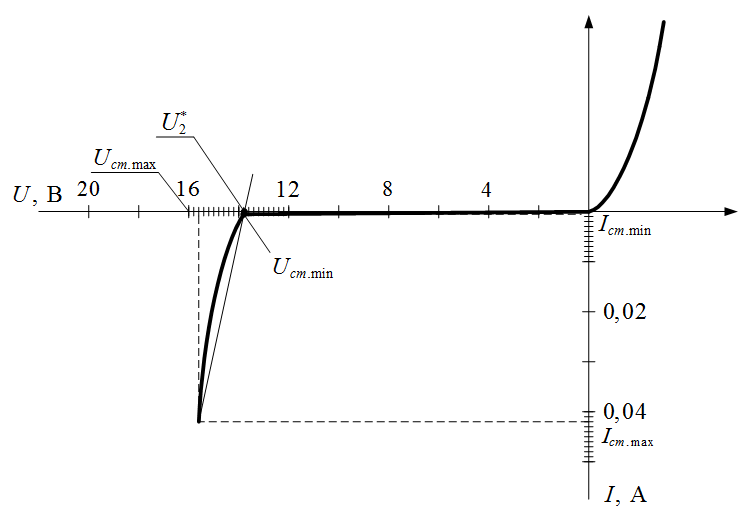
Рисунок I.14. ВАХ выбранного стабилитрона
По построенной ВАХ (рисунок I.14) определяем величину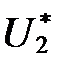 
необходимую для определения параметров схемы замещения:
Рассчитаем 
:
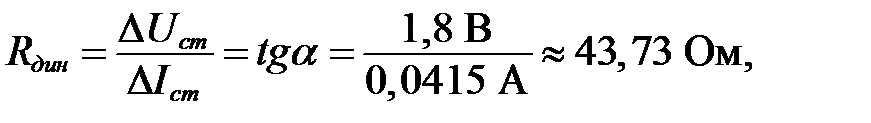
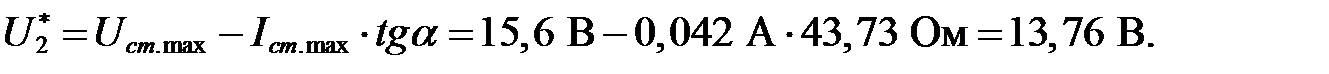
7. Проверочный расчет.
По законам Кирхгофа составим систему уравнений.
Найдем параметры схемы замещения, при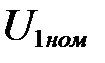 
:
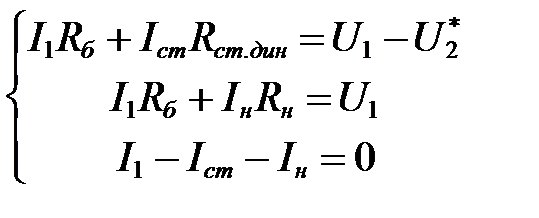
Составим матричное уравнение и найдем значения токов:
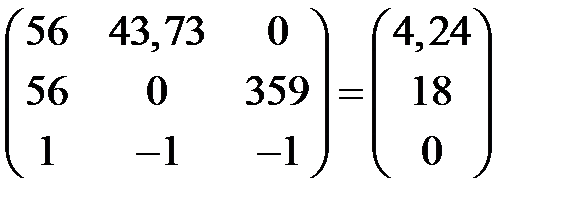
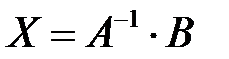
Решив матричное уравнение, получим:
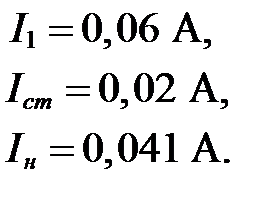
Определяем напряжение на нагрузке при номинальном заданном входном напряжении:
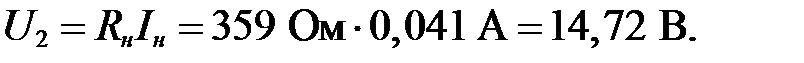
Составляем уравнения по закону Кирхгофа для входного напряжения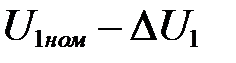 
:
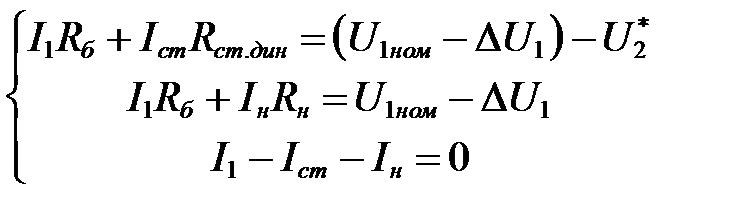
Составим матричное уравнение и найдем значения токов:
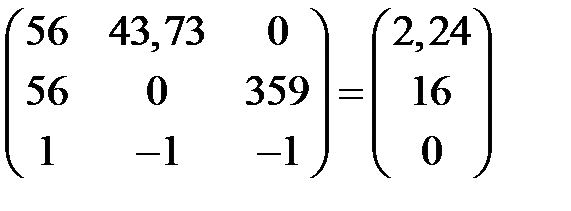
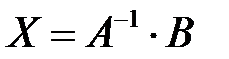
Решив матричное уравнение, получим:
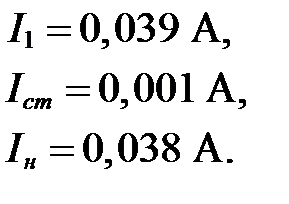
Определяем напряжение на нагрузке при минимальном заданном входном напряжении:
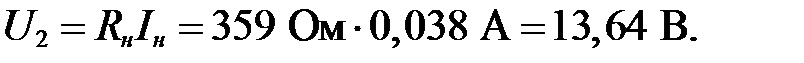
Составляем уравнения по закону Кирхгофа для входного напряжения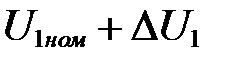 
:
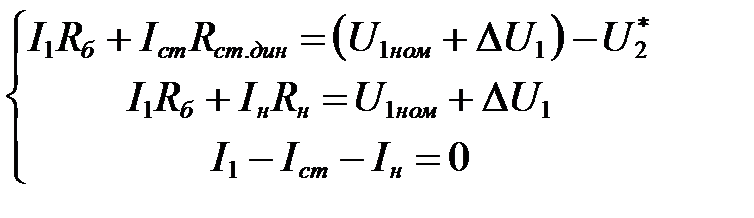
Составим матричное уравнение и найдем значения токов:
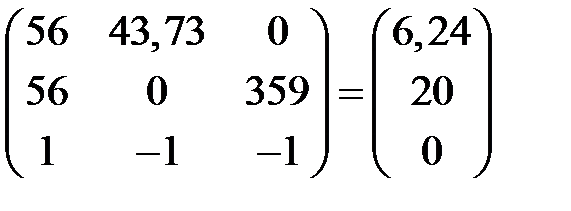
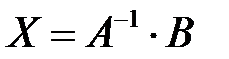
Решив матричное уравнение, получим:
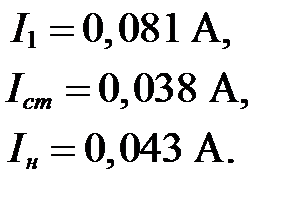
Определяем напряжение на нагрузке при максимальном заданном входном напряжении:
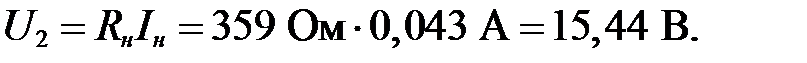
Так как в результате проверочного расчета ток через стабилитрон при максимальном входном напряжении не превышает максимальное паспортное значение тока через стабилитрон и ток через стабилитрон при минимальном входном напряжении превышает минимальное паспортное значение тока через стабилитрон выбор стабилитрона и балластного сопротивления верный. Проверочный расчет окончен.
Ответ: 1) выбран стабилитрон типа КС509А;
2) выбрано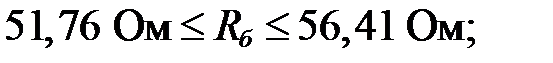 
3) уточнено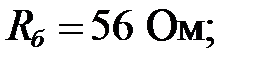 
4) 
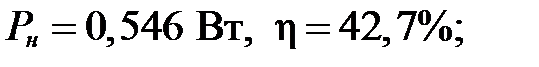
5) 
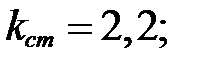
6) построена ВАХ стабилитрона (рисунок I.14);
7) Проверочный расчет подтверждает правильность выбора стабилитрона и балластного сопротивления.
ЧАСТЬ II