Задача II.2. Определить точку покоя резисторного усилителя (рисунок II.1 и рисунок II.2) на транзисторе. Характеристики транзистора приведены в приложении. Определить дифференциальный параметр h 11эв точке покоя.
Рисунок II.1. Схема резистивного усилителя для определения точки покоя
Рисунок II.2. Эквивалентная схема резистивного усилителя для определения точки покоя
Исходные данные: Тип транзистора – КТ349Б, 
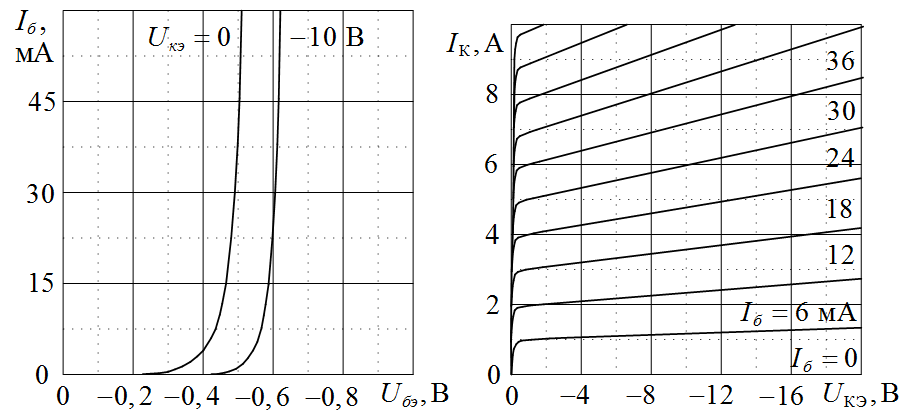
Рисунок II.3. Характеристики транзистора КТ349Б
Решение.
1. Для усилителя переменного тока, работающего в режиме класса А, точку покоя удобно определять, заменив схему эквивалентной (рисунок II.2). При этом:
Тогда, в нашем случае
Координаты пересечения нагрузочной прямой с осями в плоскости входных характеристик определяются по формулам:
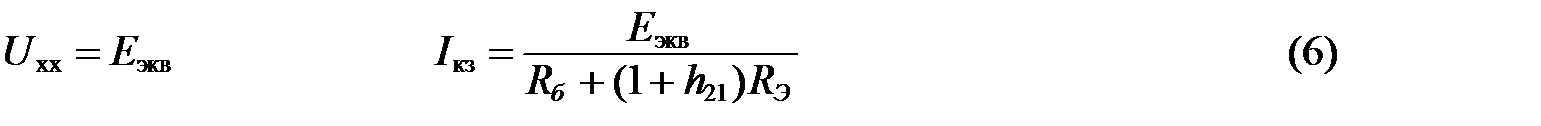
Подставив численные значения в формулы (6), получим
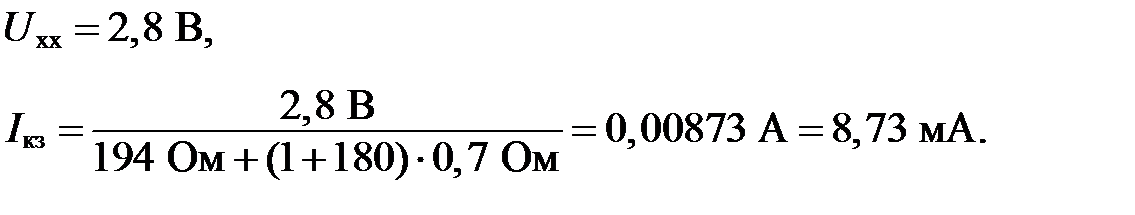
Построив нагрузочную прямую N в плоскости входных характеристик, найдем точку ее пересечения с характеристикой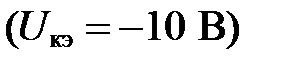 
: 
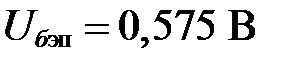(рисунок II.4).
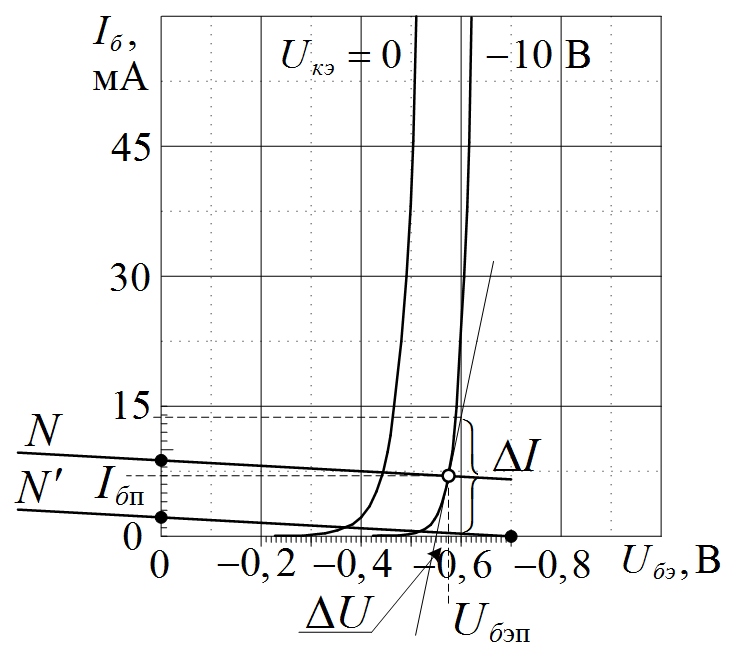
Рисунок II.4. Входная ВАХ транзистора КТ349Б
2. Находим параметр h 11э
3. Определим точки пересечения нагрузочной прямой с осями координат в плоскости выходных характеристик по формулам:
Подставив численные значения, получим:
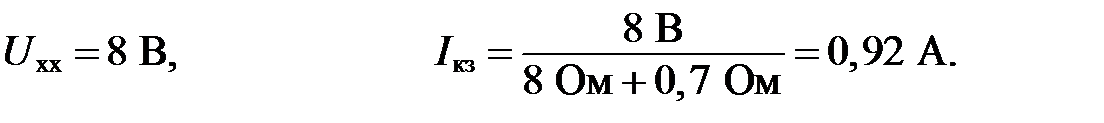
Принимая линейную аппроксимацию, строим дополнительно кривую выходной характеристики, соответствующей значению тока базы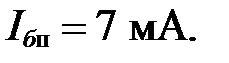 
Положение искомой точки покоя изображено на рисунке 2.5. Ей отвечают значения 
.
Рисунок II.5. Выходная ВАХ транзистора КТ349Б
Ответ: Точка покоя: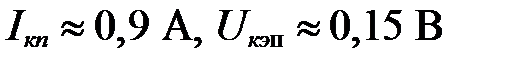 
;
Дифференциальный параметр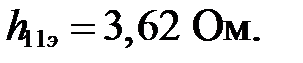 
Задача II.4. Резисторный усилитель собран на транзисторе, по схеме (рисунок II.1 и рисунок II.2). Рассчитать сопротивления R б1 и R б2. Известно, что ток через R б1 в режиме покоя в n раз больше тока I бп. Характеристики транзистора на рисунке II.3.
Исходные данные: Тип транзистора – КТ349Б, 
Решение.
…
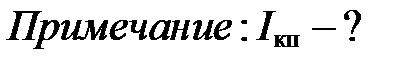Решение не найдено.
ЧАСТЬ III
Операционный усилитель
Задача III.3. Определить R ос в схеме, изображенной на рисунке III.1.
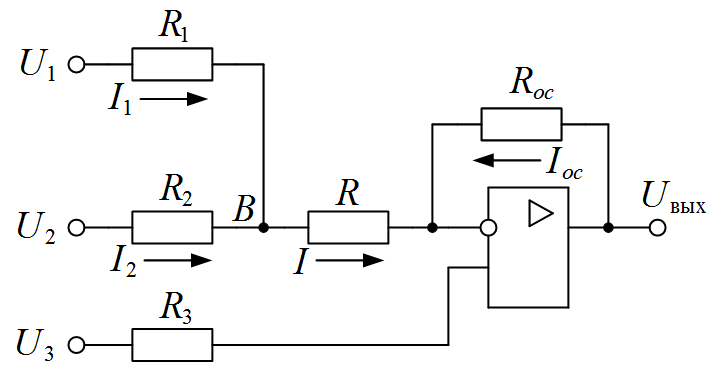
Рисунок III.1. Схема суммирования
Исходные данные: 
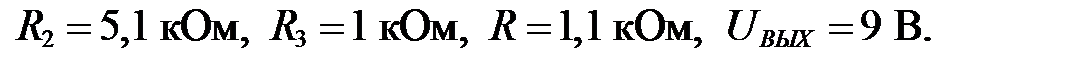
Решение.
1. Ввиду эквипотенциальности входов ОУ 
. Далее рассмотрим верхнюю часть схемы (рис. III.1).
Обозначим потенциал точки В через 
Подставив уравнения (10) в (8), получим
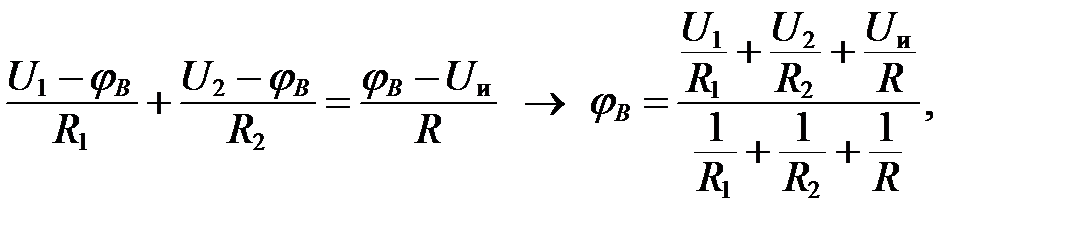тогда подставив численные значения, получим
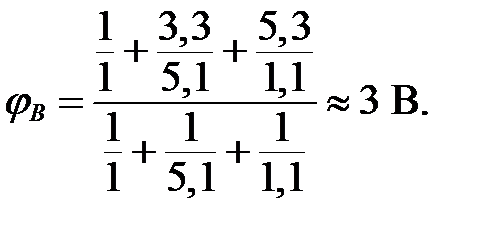
Теперь из уравнения (9) можно определить 
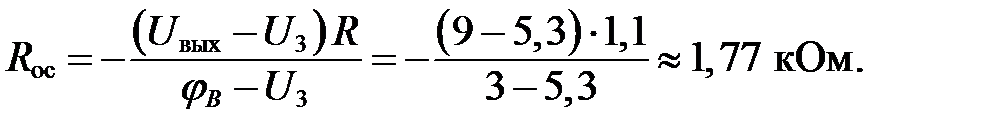
Ответ: 
Задача III.4. Определить U вых в схеме, изображенной на рисунке III.2.
Рисунок III.2. Схема суммирования
Исходные данные: 
Решение.
1. Рассмотрим нижнюю часть схемы (рисунок III.2). Для определения напряжения на неинвертирующем входе ОУ составим уравнение по первому закону Кирхгофа
или
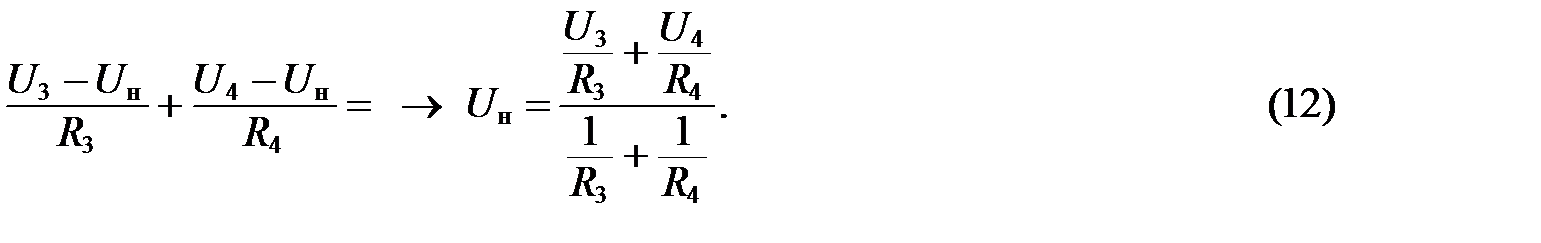
Подставив численные значения, получим:
2. Рассмотрим верхнюю часть схемы, учитывая, что 
,
и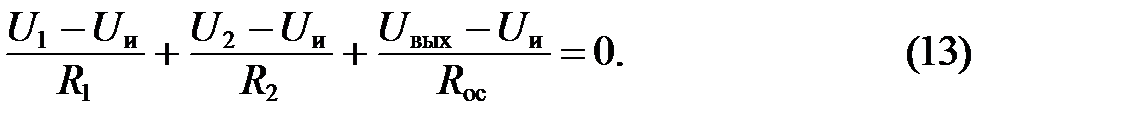 
Отсюда выражаем 
Подставив численные значения, получим:
Ответ: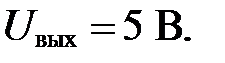 
Задача III.5. Определить R ос в схеме, изображенной на рисунке III.2.
Исходные данные: 
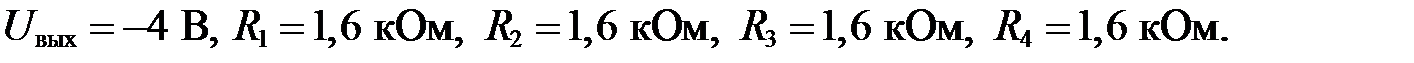
Решение.
1. Рассмотрим нижнюю часть схемы. Учитывая, что входной ток ОУ равен нулю, имеем
Воспользовавшись далее формулами (11) и (12), получим:
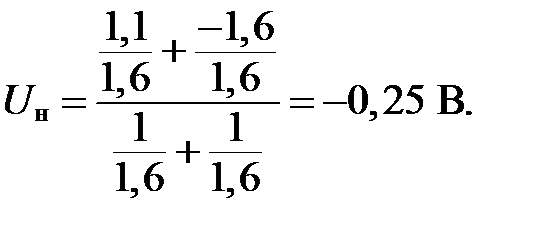
2. Считая, что 
, рассмотрим верхнюю часть схемы.
Воспользовавшись формулой (13) выразим 
Подставив численные значения, получим:
Ответ: 
Задача III.6. Определить R ос (видимо опечатка) 
в схеме, изображенной на рисунке III.3.
Исходные данные: 
Рисунок III.3. Схема суммирования
Решение.
1. Рассмотрим нижнюю часть схемы (рисунок III.3). Для определения напряжения на неинвертирующем входе ОУ составим уравнение по первому закону Кирхгофа
или
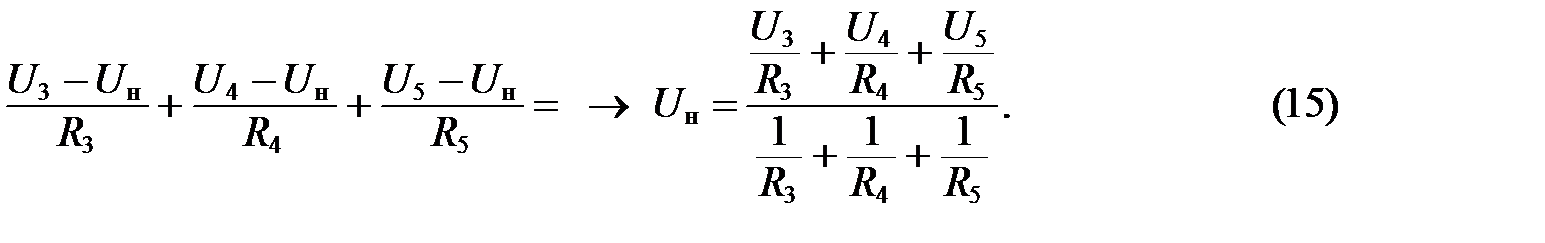
Подставив численные значения, получим:
2. Рассмотрим верхнюю часть схемы. Для решения используем формулу (10)
Тогда, подставив численные значения, получим
3. Теперь из уравнения (9) можно определить 
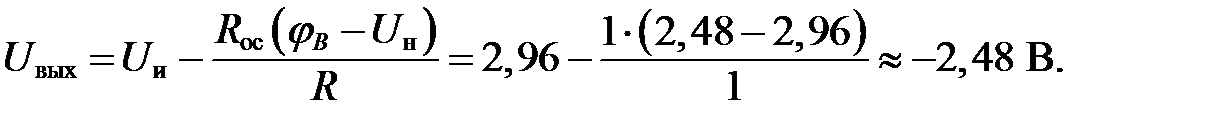
Ответ: 
Задача III.7. Определить R ос в схеме, изображенной на рисунке III.3.
Исходные данные: 
Решение.
< В задаче неизвестно сопротивление R, если конечно в методичке правильно указана расчетная схема (по методичке это схемы суммирования на рисунках 7 и 8 – они идентичны). В соответствии с [4] подобная задача решается без наличия в схеме сопротивления R >
Для заданных условий решение не найдено.
Задача III.8. Определить R 1 в схеме, изображенной на рисунке III.4.
Исходные данные: 
Рисунок III.4. Схема суммирования
Решение.
1. Решение задачи удобно начинать с рассмотрения нижней части схемы
или
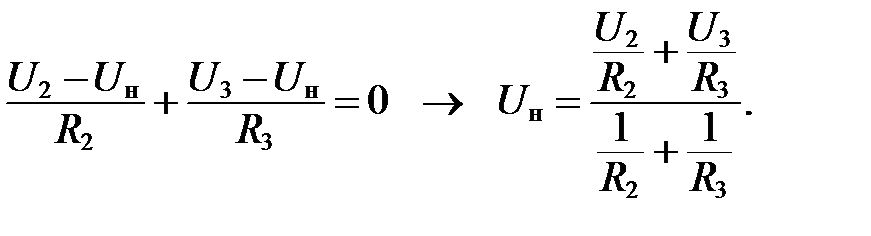
Подставив численные значения, получим:
2. Теперь рассмотрим верхнюю часть схемы, учитывая, что
,
Отсюда
Ответ: 
Задача III.11. Изобразить графически результат интегрирования на идеальном интеграторе (рисунок III.5). Входной сигнал можно представить в виде графика (рисунок III.6). Максимальное выходное напряжение ОУ равно ±10 В.
Рисунок III.5. Схема интегратора на операционном усилителе
Рисунок III.6. Напряжение на входе интегратора
Исходные данные: 
Решение.
1. Представим первый отрезок ломаной линии рисунок III.6 аналитически: 
где 
В/с, время t выражено в секундах. Напряжение на выходе ОУ при 
с можно определить согласно формуле:
где 
выражено в вольтах, а t в секундах. Отсюда:
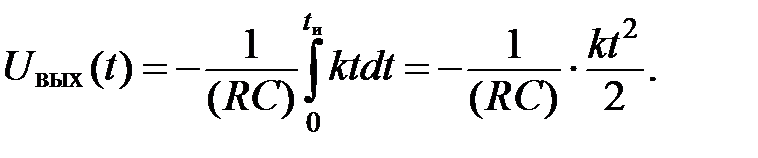
Постоянная времени 
Таким образом
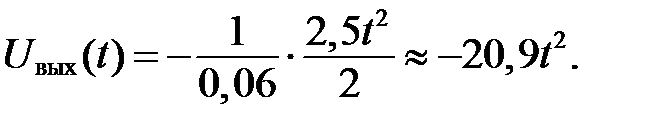
Теперь при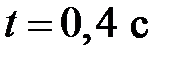 
: 
При 
: 
При 
: 
При 
: 
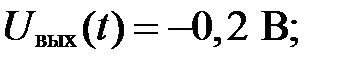
При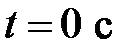 
: 
И так далее для остальных интервалов времени от 0,8 с до 2 с.
Ответ: Изобразим графически результат интегрирования на рис. III.7.
Рисунок III.7. График напряжения на выходе интегратора
Задача III.12. Изобразить графически результат интегрирования на идеальном интеграторе (рисунок III.5), если 
а входной сигнал можно представить в виде графика (рисунок III.8). Максимальное выходное напряжение ОУ равно ± 11 В. Определить результат интегрирования при 
< В методичке, видимо, ошибка в задании, так как исходные данные уже представлены в задаче, а в тексте присутствует ссылка на "таблицу 7" (в методичке). В решении ссылка на "таблицу 7" учитываться не будет >
Рисунок III.8. Напряжение на входе интегратора
Указание. Можно упростить решение, если учесть, что определенный интеграл численно равен площади под кривой.
Решение.
1. Представим первый отрезок ломаной линии рисунок III.8 аналитически: 
где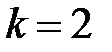 
В/с, время t выражено в секундах. Напряжение на выходе ОУ при 
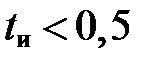с определяем согласно формуле (16):
Постоянная времени 
Таким образом
Представим аналогичным образом второй отрезок ломаной линии (рисунок III.8): 
где 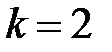В/с. Тогда по формуле (16), получим:
Таким образом
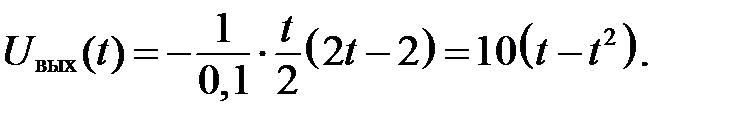
Теперь при 
: 
При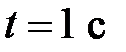 
: 
При 
: 
При 
: 
При 
: 
При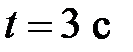 
: 
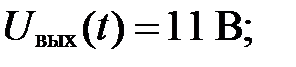
Ответ: Изобразим графически результат интегрирования на рис. III.9.
Рисунок III.9. График напряжения на выходе интегратора
Задача III.13. Изобразить график 
на интеграторе (рисунок III.5) при входных напряжениях, заданных диаграммами на рисунке III.10 и на рисунках III.11, а и б. Если заданы параметры 
, С и максимальное выходное напряжение 
ОУ. Операционный усилитель считать идеальным.
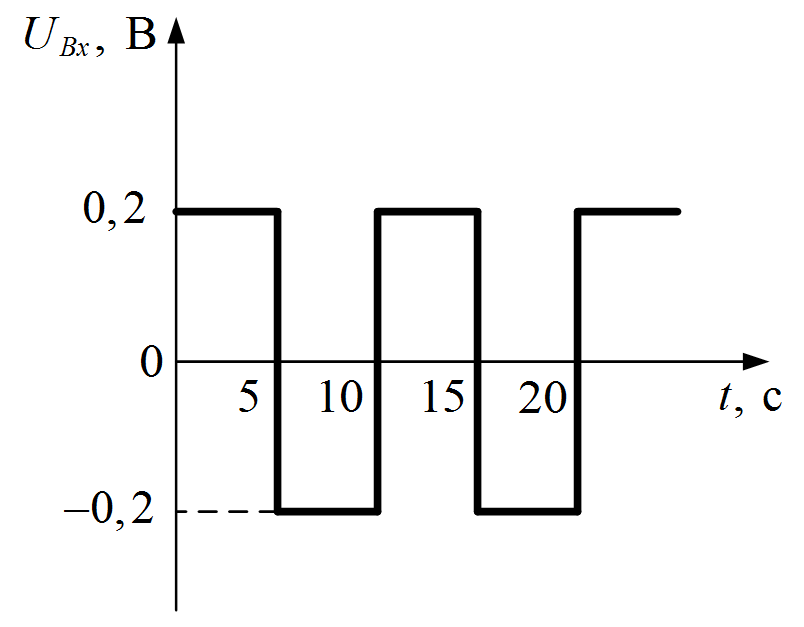
Рисунок III.10. Напряжение на входе интегратора
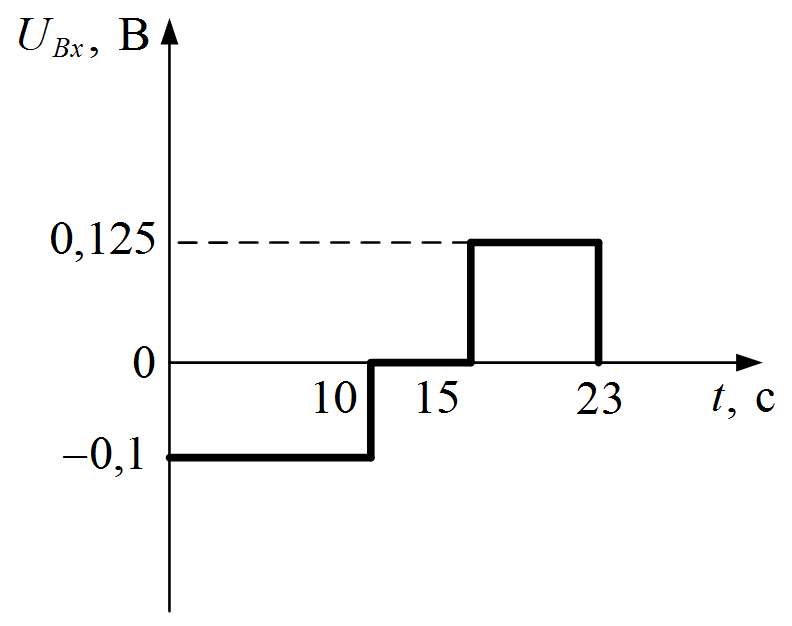
а)
б)
Рисунок III.11 а, б. Напряжение на входе интегратора
Исходные данные: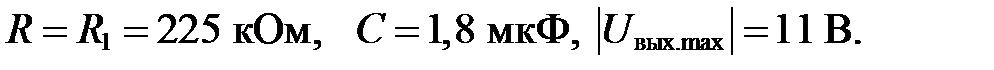 
Решение.
1. Определяем напряжение на выходе ОУ для первой прямой на графике (рис. III.10) согласно формуле (16):
Для второй прямой (рис. III.10), соответствующей отрицательному входному напряжению:
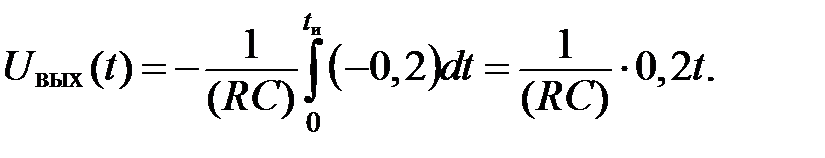
Постоянная времени 
Тогда для первой прямой 
(точки: -0,5; -1; -1,5; -2; -2,5; -3; -3,5; -4; -4,5; -5)
Для второй прямой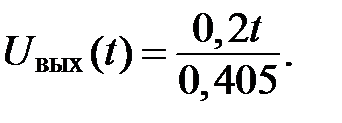 
(точки: 0,5; 1; 1,5; 2; 2,5; 3; 3,5; 4; 4,5; 5)
2. Определяем напряжение на выходе ОУ для первой прямой на графике (рис. III.11, а) согласно формуле (16):
Для второй прямой (рис. III.11, а), соответствующему положительному значению входного напряжения:
Тогда для первой прямой 
(точки: 0,25; 0,5; 0,75; 1; 1,25; 1,5; 1,75; 2; 2,25; 2,5)
Для второй прямой 
(точки: -0,3; -0,6; -0,9; -1,2; -1,5; -1,85; -2,2; -2,5)
3. Определяем напряжение на выходе ОУ для первой прямой на графике (рис. III.11, б) согласно формуле (16):
(точки: 1,2; 2,5; 3,7; 5; 6,2; 7,4; 8,6; 9,9; 11,1; 12,3)
Для второй прямой (рис. III.11, а), соответствующему положительному значению входного напряжения:
(точки: -12,3)
Ответ: Изобразим графически результат интегрирования на рис. III.12.
а) (для пункта 1 задачи)
б) (для пункта 2 задачи)
в) (для пункта 3 задачи)
Задача III.15. Определить напряжение на выходе идеального интегратора U вых(t) (рисунок III.13). U 2 изменяется в соответствии с графиком (рисунок III.14).
Исходные данные: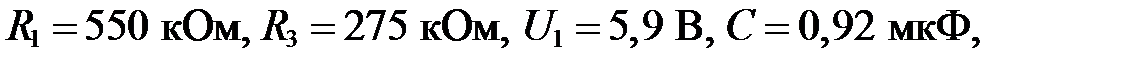 
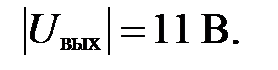
Рисунок III.13. Схема интегратора
Рисунок III.14. Напряжение на входе интегратора
Решение.
1. Из рисунка III.13 следует 
или
Следовательно, для идеального операционного усилителя
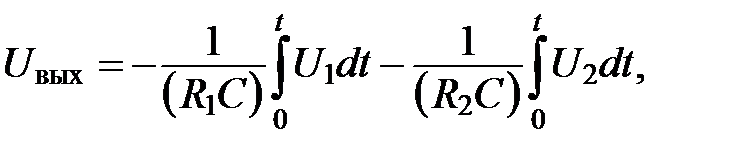
где 
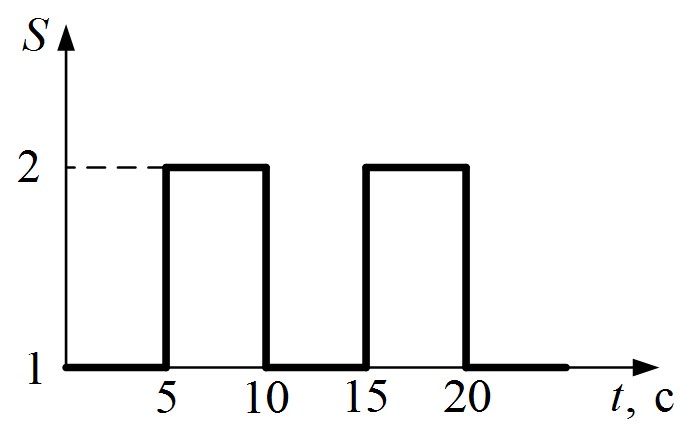
Задача III.16. Построить диаграммы напряжения U вых(t) идеального интегратора (рисунок III.15, а), на вход которого подается постоянное напряжение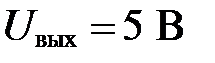 
. Ключ S коммутируется с частотой 100 переключений в секунду. Диаграммы U вых (t) построить для функций коммутации ключа S, соответствующих рисунку III.15, б и рисунку III.15, в. 
.
а)
б)
в)
Рисунок III.15. Схема интегратора и функции коммутации ключа
Исходные данные: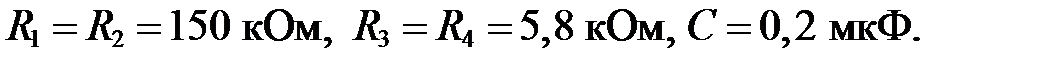 
Решение.
Задача III.17. На затвор транзистора VT (рисунок III.16, а) подается импульсное управляющее напряжение U (t). Величина U 0 превышает пороговое напряжение транзистора VT. Построить диаграммы U вых(t) идеального интегратора, если U (t) изменяется согласно рисунку III.16, б и в. Параметры элементов схемы интегратора: 
, 
, 
. Сопротивлением транзистора в открытом состоянии пренебречь, в закрытом состоянии сопротивление транзистора считать бесконечно большим.
/ Указание. Напряжение на входах идеального ОУ равно 
и при постоянном U вх не зависит от времени. /
а)
б)
в)
Рисунок III.16. Схема интегратора и диаграммы управляющего напряжения
Решение.