Свойства граней и диагоналей параллелепипеда.

МНОГОГРАННИКИ

Геометрическим телом называется ограниченная со всех сторон часть пространства. То, что отделяет геометрическое тело от остальной части пространства, называется поверхностью тела.

Многогранник – это тело, ограниченное со всех сторон плоскими многоугольниками, которые называются гранями. Общие стороны граней называются рёбрами многогранника (AB, AA₁, A₁D₁, …); точки, в которых сходятся три и более граней, - вершинами (A, A₁, D, …). Отрезок, соединяющий две вершины, не принадлежащие к одной грани, называется диагональю.

При каждом ребре многогранника образуется двугранный угол; при каждой вершине – фигура, составленная из плоских углов граней, которая называется многогранным углом.

Призма

Призма – это многогранник, у которого две грани, называемые основаниями, - равные многоугольники с соответственно параллельными сторонами, а остальные грани (боковые) – параллелограммы, вершинами которых являются концы соответственно параллельных и равных сторон оснований. Рёбра (AA₁, BB₁, CC₁, …), соединяющие соответственно вершины оснований, называются боковыми ребрами призмы. Все боковые ребра призмы равны между собой (как отрезки параллельных прямых, заключённые между параллельными плоскостями).

Перпендикуляр (M₁M), опущенный из любой точки одного основания на плоскость другого основания, называется высотой призмы. Призма называется n – угольной, если в основании её лежит n – угольник.

Призма называется прямой, если её боковое ребро перпендикулярно плоскости основания. Все боковые грани прямой призмы – прямоугольники. Всякая непрямая призма называется наклонной. Прямая призма называется правильной, если её основанием является правильный многоугольник.

Поверхность призмы.

Под поверхностью призмы подразумевается число, равное сумме площадей всех граней призмы. Различают боковую () и полную () поверхность призмы.

Боковая поверхность призмы – это сумма площадей всех её боковых граней; а полная поверхность равна сумма боковой поверхности и удвоенной площади основания:

.

Вычисление боковой поверхности призмы связано с понятием перпендикулярного сечения призмы. Таким сечением называют многоугольник, который получается при пересечении плоскостей боковых граней призмы плоскостью, перпендикулярной её боковому ребру.

Теорема. Боковая поверхность призмы равна произведению периметра перпендикулярного сечения на боковое ребро: .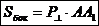

Следствие. Боковая поверхность прямой призмы равна произведению периметра основания на высоту: .

Объём призмы равен произведению площади её основания на высоту: .

Параллелепипед

Призма, в основании которой лежит параллелограмм, называется параллелепипедом. Параллелепипеды, как и призмы, могут быть наклонными и прямыми. Прямой параллелепипед, в основании которого лежит прямоугольник, называется прямоугольным. У такого параллелепипеда все грани – прямоугольники. Три ребра прямоугольного параллелепипеда, сходящиеся в одной вершине (D), называются его измерениями.

Прямоугольный параллелепипед с равными измерениями называется кубом.

Свойства граней и диагоналей параллелепипеда.

Теорема 1. Во всяком параллелепипеде противоположные грани параллельны и равны.

Теорема 2. Во всяком параллелепипеде все четыре диагонали пересекаются в одной точке и делятся в ней пополам.

Теорема 3. В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений: .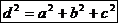

Следствие. Все четыре диагонали прямоугольного параллелепипеда равны между собой.

Теорема. Объём всякого параллелепипеда равен произведению площади его основанию на высоту: .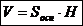

Объём прямоугольного параллелепипеда равен произведению трёх его измерений:

,

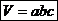где a, b и c – измерения параллелепипеда.

Пирамида

Пирамидой называется многогранник, у которого одна грань (основание) – многоугольник, а остальные грани (боковые) – треугольники с общей вершиной, которая называется вершиной пирамиды.

В зависимости от числа сторон (углов) основания пирамида может быть треугольной, четырёхугольной и т.д. Треугольную пирамиду называют тетраэдром.

Теорема 1. Если все боковые ребра пирамиды равны между собой, то они одинаково наклонены к плоскости основания.

Следствие. Точка O – центр окружности, описанной около основания.

Справедлива обратная теорема: если все боковые ребра пирамиды одинаково наклонены к плоскости основания, то они равны между собой.

Таким образом, если все боковые ребра пирамиды равны между собой или одинаково наклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности, описанной около основания.

Теорема 2. Если все двугранные углы при основании пирамиды равны между собой, то равны между собой высоты всех боковых граней.

Следствие. Точка O равноудалена от всех сторон основания, т.е. является центром окружности, вписанной в основание.

Справедлива обратная теорема: если высоты всех боковых граней пирамиды равны между собой, то равны все двугранные углы при основании.

Таким образом, если все двугранные углы при основании равны между собой (или равны высоты всех боковых граней), то вершина пирамиды проектируется в центр окружности, вписанной в основание.

Пирамида, в основании которой лежит правильный многоугольник, а вершина проектируется в центр основания, называется правильной.

Из определения следует, что правильная пирамида обладает следующими свойствами:

1. Все боковые ребра правильной пирамиды равны между собой.

2. Все боковые грани правильной пирамиды – равные равнобедренные треугольники.

3. Боковые ребра правильной пирамиды равнонаклонены к плоскости основания.

4. В правильной пирамиде двугранные углы при основании равны.

5. Высоты боковых граней, называемые апофемами правильной пирамиды, равны между собой.